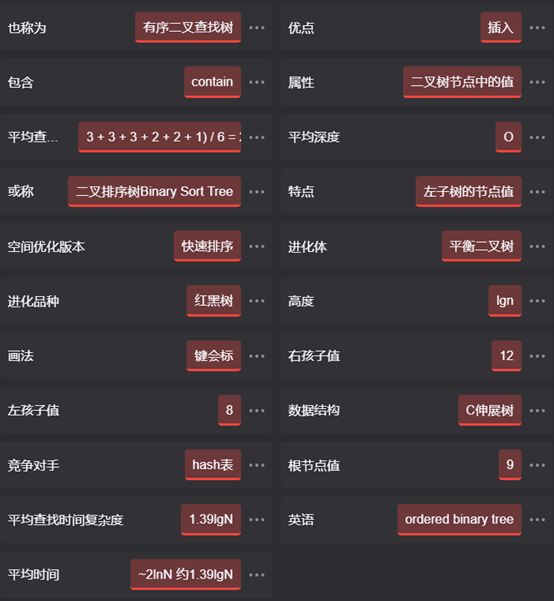
二分搜索树属性
二分搜索树的又名比较多,有的叫二叉排序树,也有的叫二叉查找树,或者有序二叉查找树。是指一棵空树或者具有下列性质的二叉树:
1.若任意节点的左子树不空,则左子树所有节点的值均小于它根节点的值;
2.若任意节点的右子树不空,则右子树所有节点的值均小于它根节点的值;
3.任意节点的左、右子树也分别为二叉查找树;
4.没有键值相等的节点。
它的查找、插入和删除的时间复杂度都等于树高,期望值是O(logn),最坏时间复杂度是O(n),比如树退化成线性表。
(响应读者的建议,视频动画不放BGM了)
查找元素
二分搜索树是为了实现快速查找而生的,也支持快速添加和删除一个数据。如何查找某个元素首先跟根节点去做比较,如果相等的话就返回;如果待查元素要比根节点小,就进行左子树递归查找;如果待查元素要比根节点大,就进行右子树的递归查找;如果查找到最后还没有一个符合的元素,就返回null。
递归查找
递归查找的方式有很多,有层序遍历、前序遍历、中序遍历和后序遍历。我这里就举后面三个遍历方式。
Code
如果代码是下面这样写的,那它遍历过程是怎么样的?看下面视频动画。
视频动画:前序遍历
视频动画:前中后遍历
视频动画:前中后遍历 前序
视频动画:前中后遍历 中序
经过中序遍历得到的正好是一个升序序列。
视频动画:前中后遍历 后序
如果不考虑升序,后序遍历能够为二分搜索树早点释放内存。
添加元素
对于二叉树的添加和删除元素,使用链表存储形式比较好操作的,如果使用数组形式存储,删除某一个有子树的元素会引发一系列的位置改变,涉及到交换元素的位置,性能也比链表的小。所以待会后面出现的伪代码都以链表存储形式去操作。
视频动画:添加元素
Code
删除元素:删除最小和最大的元素
删除最小和最大的元素很简单,如果是删除最小的元素,从二叉树的顶点出发,一直递归它的左孩子,直到某节点的左孩子为空,这时候这个节点就是最小的元素。删除最大的元素也是一样的,一直递归它的右孩子,直到某节点的右孩子为空。
视频动画:删除最小和最大的元素
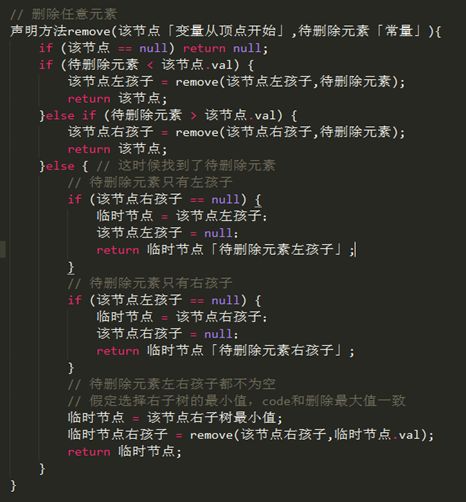
删除任意元素
如果删除任意元素,而这元素正好有左右子树的,那该是怎么般呢?
1962年,Hibbard提出了Hibbard Deletion的解决方法。
看到Hibbard名字就想起来,我在希尔排序介绍过Hibbard增量序列,也把它相应的公式通过代码体现出来,代替希尔增量序列去进行希尔排序,最坏时间复杂度也比希尔增量序列的要小。
回到删除有左右子树的元素,想想它的左右子树也属于二叉排序树(也是二分搜索树),它左子树的最大值比它小,它右子树的最小值比它大。所以不管选择左子树的最大值还是选择右子树的最小值,替换掉要删除的元素,整个二叉树都是符合二分搜索树的规则。
视频动画:删除任意元素
Code
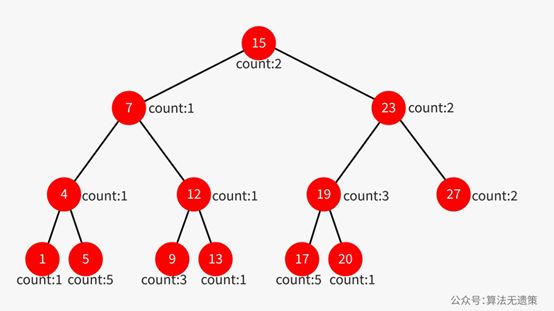
支持重复元素的二分搜索树
二分搜索树有一个规则是:没有键值相等的节点。那么就不建议把待添加的元素跳过值相等的节点,到下一步继续比较直到插入新的节点。比如我想插入23,插完之后上有23,下有23,那查找就没有意义了,也破坏了时间复杂度上的O(logn)。
建议就是在节点上加一个属性:count。当插入23的时候,count就可以自算++。这不仅满足了没有键值相等的规则,也满足时间复杂度的期望值。