- Tags:
算法棋盘覆盖问题
【问题描述】
在一个2^k×2^k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何k≥0,有4^k种不同的特殊棋盘.
下图中的特殊棋盘是当k=3时64个特殊棋盘中的一个:
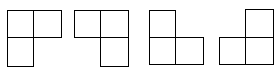
在棋盘覆盖问题中,要用下图中 4 中不同形态的** L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖**。易知,在任何一个 2^k × 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
用分治策略,可以设计解棋盘问题的一个简捷的算法。
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,如下图所示:
特殊方格必位于 4 个较小子棋盘之一中,其余 3 个子棋盘中无特殊方格。
为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处,如下图所示,这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。
递归的使用这种分割,直至棋盘简化为 1x1 棋盘。
【算法实现】
下面讨论棋盘覆盖问题中数据结构的设计:
(1)棋盘:可以用一个二维数组board[size][size]表示一个棋盘,其中,size=2^k。为了在递归处理的过程中使用同一个棋盘,将数组board设为全局变量;
(2)子棋盘:整个棋盘用二维数组board[size][size]表示,其中的子棋盘由棋盘左上角的下标tr、tc和棋盘大小s表示;
(3)特殊方格:用board[dr][dc]表示特殊方格,dr和dc是该特殊方格在二维数组board中的下标;
(4) L型骨牌:一个2k×2k的棋盘中有一个特殊方格,所以,用到L型骨牌的个数为(4^k-1)/3,将所有L型骨牌从1开始连续编号,用一个全局变量t表示。
【算法分析】
设T(k)是算法ChessBoard覆盖一个2k×2k棋盘所需时间,从算法的划分策略可知,T(k)满足如下递推式:
T(k) = 1 当k=0时
T(k) = 4 * T(k-1) 当k>0时
解此递推式可得 T(k) = O(4^k)。
【C语言代码】
#include
#define BOARD_SIZE 4
int board[BOARD_SIZE][BOARD_SIZE];
// c1, r1: 棋盘左上角的行号和列号
// c2, r2: 特殊方格的行号和列号
// size = 2 ^ k
void chessboard(int r1, int c1, int r2, int c2, int size)
{
if(1 == size) return;
int half_size;
static int domino_num = 1;
int d = domino_num++;
half_size = size / 2;
if(r2 < r1 + half_size && c2 < c1 + half_size) //特殊方格在左上角子棋盘
{
chessboard(r1, c1, r2, c2, half_size);
}
else // 不在此棋盘,将此棋盘右下角设为相应的骨牌号
{
board[r1 + half_size - 1][c1 + half_size - 1] = d;
chessboard(r1, c1, r1 + half_size - 1, c1 + half_size - 1, half_size);
}
if(r2 < r1 + half_size && c2 >= c1 + half_size) //特殊方格在右上角子棋盘
{
chessboard(r1, c1 + half_size, r2, c2, half_size);
}
else // 不在此棋盘,将此棋盘左下角设为相应的骨牌号
{
board[r1 + half_size - 1][c1 + half_size] = d;
chessboard(r1, c1 + half_size, r1 + half_size - 1, c1 + half_size, half_size);
}
if(r2 >= r1 + half_size && c2 < c1 + half_size) //特殊方格在左下角子棋盘
{
chessboard(r1 + half_size, c1, r2, c2, half_size);
}
else // 不在此棋盘,将此棋盘右上角设为相应的骨牌号
{
board[r1 + half_size][c1 + half_size - 1] = d;
chessboard(r1 + half_size, c1, r1 + half_size, c1 + half_size - 1, half_size);
}
if(r2 >= r1 + half_size && c2 >= c1 + half_size) //特殊方格在左上角子棋盘
{
chessboard(r1 + half_size, c1 + half_size, r2, c2, half_size);
}
else // 不在此棋盘,将此棋盘左上角设为相应的骨牌号
{
board[r1 + half_size][c1 + half_size] = d;
chessboard(r1 + half_size, c1 + half_size, r1 + half_size, c1 + half_size, half_size);
}
}
int main()
{
int i, j;
board[2][2] = 0;
chessboard(0, 0, 2, 2, BOARD_SIZE);
for(i = 0; i < BOARD_SIZE; i++)
{
for(j = 0; j < BOARD_SIZE; j++)
{
printf("%-4d", board[i][j]);
}
printf("\n");
}
}
【C++代码1】
#include
using namespace std;
int tile=1; //L型骨牌的编号(递增)
int board[100][100]; //棋盘
/*****************************************************
* 递归方式实现棋盘覆盖算法
* 输入参数:
* tr--当前棋盘左上角的行号
* tc--当前棋盘左上角的列号
* dr--当前特殊方格所在的行号
* dc--当前特殊方格所在的列号
* size:当前棋盘的:2^k
*****************************************************/
void chessBoard ( int tr, int tc, int dr, int dc, int size )
{
if ( size==1 ) //棋盘方格大小为1,说明递归到最里层
return;
int t=tile++; //每次递增1
int s=size/2; //棋盘中间的行、列号(相等的)
//检查特殊方块是否在左上角子棋盘中
if ( dr=tc+s ) //在
chessBoard ( tr, tc+s, dr, dc, s );
else //不在,将该子棋盘左下角的方块视为特殊方块
{
board[tr+s-1][tc+s]=t;
chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
}
//检查特殊方块是否在左下角子棋盘中
if ( dr>=tr+s && dc=tr+s && dc>=tc+s ) //在
chessBoard ( tr+s, tc+s, dr, dc, s );
else //不在,将该子棋盘左上角的方块视为特殊方块
{
board[tr+s][tc+s]=t;
chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
}
}
void main()
{
int size;
cout<<"输入棋盘的size(大小必须是2的n次幂): ";
cin>>size;
int index_x,index_y;
cout<<"输入特殊方格位置的坐标: ";
cin>>index_x>>index_y;
chessBoard ( 0,0,index_x,index_y,size );
for ( int i=0; i 【C++代码2】
#include
#include
#include
using namespace std;
vector > board(4);//棋盘数组,也可以作为参数传递进chessBoard中去,作为全局变量可以减少参数传递
stack stI; //记录当前所使用的骨牌号码,使用栈顶元素填充棋盘数组
int sL = 0; //L型骨牌序号
//所有下标皆为0开始的C C++下标
void chessBoard(int uRow, int lCol, int specPosR, int specPosC, int rowSize)
{
if(rowSize ==1) return;
//static int sL = 0;棋牌和骨牌都可以用static代替,如果不喜欢用全局变量的话。
sL++;
stI.push(sL); //每递归深入一层,就把一个骨牌序号入栈
int halfSize = rowSize/2;//拆分
//注意:下面四个if else,肯定是只有一个if成立,然后执行if句,而肯定有三个else语句要执行的,因为肯定有一个是特殊位置,而其他三个是空白位置,需要填充骨牌。
//1如果特殊位置在左上角区域,则继续递归,直到剩下一个格子,并且该格子已经填充,遇到函数头一句if(rowSize == 1) return;就跳出一层递归。
//注意是一个区域或子棋盘,有一个或者多个格子,并不是就指一个格子。
if(specPosR=lCol+halfSize)
chessBoard(uRow, lCol+halfSize, specPosR, specPosC, halfSize);
else
{
board[uRow+halfSize-1][lCol+halfSize] = stI.top();
chessBoard(uRow, lCol+halfSize, uRow+halfSize-1, lCol+halfSize, halfSize);
}
//3左下角区域,类上
if(specPosR>=uRow+halfSize && specPosC=uRow+halfSize && specPosC>=lCol+halfSize)
chessBoard(uRow+halfSize, lCol+halfSize, specPosR, specPosC, halfSize);
else
{
board[uRow+halfSize][lCol+halfSize] = stI.top();
chessBoard(uRow+halfSize, lCol+halfSize, uRow+halfSize, lCol+halfSize, halfSize);
}
stI.pop();//本次骨牌号填充了三个格,填充完就出栈
}
void test()
{
//初始化数组
for(int i=0; i<4; i++)
{
board[i].resize(4);
}
chessBoard(0, 0, 3, 3, 4);
//特殊位置填充0
board[3][3] = 0;
//序列输出
for(int j=0; j<4; j++)
{
for(int i=0; i<4; i++)
cout< 【JAVA】
1、Element类,它有两个属性,一个是JPanel,它主要用来显示一个小格的颜色;另一个属性是flag,它用来标记此方格有没有被填充过。另外Element之所以要继承Jcomponent,是因为我们要把Element加入到JFrame当中去。因此具体代码如下:
package com.qipan.test;
import javax.swing.JComponent;
import javax.swing.JPanel;
public class Element extends JComponent {
private static final long serialVersionUID = 1L;
private JPanel j;
boolean flag = false;
public Element() {
this.j = new JPanel();
}
public JPanel getJ() {
return j;
}
public void setJ(JPanel j) {
this.j = j;
}
public boolean isFlag() {
return flag;
}
public void setFlag(boolean flag) {
this.flag = flag;
}
}
2、Application主类的设计:首先在它里面有一个JFrame,然后对它进行网格布局,对每个小的布局区域里我们加入一个Element元素,注意覆盖的时候都是按三格L型来操作的。具体算法如下:
(1)把全部方格分成4个区域,若其中一个区域中有被覆盖过的,则从其他域中各选一个构成三格L型进行着色。
(2)对上面分完后的每个区域,我们再同上一样进行那样的一次着色过程。
(3)到一定程度时,我们要退出着色过程,也就是递归的出口。
此类的源代码如下:
package com.qipan.test;
import java.awt.Color;
import java.awt.GridLayout;
import java.util.Random;
import javax.swing.JFrame;
public class Application extends JFrame {
private static final long serialVersionUID = 1L;
int size = 16;
private Element[][] elements = new Element[size][size];
Color[] colors = new Color[220];
JFrame jf = new JFrame();
public void makeColor() {
int num = 0;
for (int i = 0; i < 255; i += 50)
for (int j = 0; j < 255; j += 50)
for (int k = 0; k < 255; k += 50) {
Color c = new Color(i, j, k);
colors[num++] = c;
}
}
public Application() {
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++) {
elements[i][j] = new Element();
}
}
public void create() {
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++) {
jf.add(elements[i][j].getJ());
}
jf.setVisible(true);
jf.setSize(512, 512);
jf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
public void paintFrame() {
makeColor();
elements[6][10].setFlag(true);
jf.setLayout(new GridLayout(size, size));
search(0, 0, size);
}
public void search(int m, int n, int length) {
if (length == 1)
return;
int subLength = length / 2;
int n1 = 0, n2 = 0, n3 = 0, n4 = 0;
for (int i = 0; i < subLength; i++)
for (int j = 0; j < subLength; j++) {
if (elements[m + i][n + j].isFlag())
n1++;
if (elements[m + i][n + subLength + j].isFlag())
n2++;
if (elements[m + subLength + i][n + j].isFlag())
n3++;
if (elements[m + subLength + i][n + subLength + j].isFlag())
n4++;
}
Random r = new Random();
int color_num = r.nextInt(216);
Color c = colors[color_num];
if (n1 == 1) {
elements[m + subLength - 1][n + subLength].getJ().setBackground(c);
elements[m + subLength][n + subLength - 1].getJ().setBackground(c);
elements[m + subLength][n + subLength].getJ().setBackground(c);
elements[m + subLength - 1][n + subLength].setFlag(true);
elements[m + subLength][n + subLength - 1].setFlag(true);
elements[m + subLength][n + subLength].setFlag(true);
}
if (n2 == 1) {
elements[m + subLength - 1][n + subLength - 1].getJ()
.setBackground(c);
elements[m + subLength][n + subLength - 1].getJ().setBackground(c);
elements[m + subLength][n + subLength].getJ().setBackground(c);
elements[m + subLength - 1][n + subLength - 1].setFlag(true);
elements[m + subLength][n + subLength - 1].setFlag(true);
elements[m + subLength][n + subLength].setFlag(true);
}
if (n3 == 1) {
elements[m + subLength - 1][n + subLength - 1].getJ()
.setBackground(c);
elements[m + subLength - 1][n + subLength].getJ().setBackground(c);
elements[m + subLength][n + subLength].getJ().setBackground(c);
elements[m + subLength - 1][n + subLength - 1].setFlag(true);
elements[m + subLength - 1][n + subLength].setFlag(true);
elements[m + subLength][n + subLength].setFlag(true);
}
if (n4 == 1) {
elements[m + subLength - 1][n + subLength - 1].getJ()
.setBackground(c);
elements[m + subLength - 1][n + subLength].getJ().setBackground(c);
elements[m + subLength][n + subLength - 1].getJ().setBackground(c);
elements[m + subLength - 1][n + subLength - 1].setFlag(true);
elements[m + subLength - 1][n + subLength].setFlag(true);
elements[m + subLength][n + subLength - 1].setFlag(true);
}
try {
Thread.sleep(200);
} catch (InterruptedException e) {
System.out.println(e);
}
create();
search(m, n, subLength);
search(m, n + subLength, subLength);
search(m + subLength, n, subLength);
search(m + subLength, n + subLength, subLength);
}
public static void main(String[] args) {
Application app = new Application();
app.paintFrame();
}
}
程序的最终效果:
Reference:
[1] http://blog.csdn.net/akof1314/article/details/5423608
[2] http://www.cnblogs.com/kahreman/archive/2011/08/08/2130613.html
[3] http://www.iamyoso.com/?p=393
[4] http://blog.sina.com.cn/s/blog_7476a4db0100wpk1.html
[5] http://www.cnblogs.com/nokiaguy/archive/2008/05/11/1192579.html
[6] http://blog.chinaunix.net/uid-26548237-id-3505163.html
[7] http://www.2cto.com/kf/201310/252188.html
[8] http://baike.baidu.com/link?url=7fqQcXwuMNpTL-oASXVdI6PH11tg1vpkbIQBWKgOOeFW7SMypkyXbSm3huRwt0-JNQ6UDnB858AFDmmFnSMTka
[9] http://blog.sina.com.cn/s/blog_67cf65ab0100qt4z.html
(注:感谢您的阅读,希望本文对您有所帮助。如果觉得不错欢迎分享转载,但请先点击 这里 获取授权。本文由 版权印 提供保护,禁止任何形式的未授权违规转载,谢谢!)