< 算法笔记（晴神宝典) - 读书笔记 >

< 算法笔记（晴神宝典) - 读书笔记 >

第二章：C++快速入门

2.5 数组

• memset - 对数组中每一个元素赋相同的值 - 用于初始化 / 重置

  • memset(数组名,值,sizeof(数组名));

  • 一般初始化 0 或者 -1 ，因为memset使用的是按字节赋值，这样int类型的4个字节都会被赋成相同的值。

  • 若要对数组赋为其他数字 - 使用STL中的fill函数

• string.h头文件函数
  • strlen(字符数组);
    • 得到字符数组中第一个\0前的字符个数
  • strcmp(字符数组1,字符数组2);
    • 返回两个字符串大小比较结果，比较原则是按字典序 - <返回负整数 =返回0 >返回正整数
  • strcpy(字符数组1,字符数组2)；
    • 把字符数组2复制给字符数组1 - 包括结束符\0
  • strcat(字符数组1,字符数组2)
    • 把字符数组2拼接到字符数组1后
• sscanf & sprintf
  • string+ scanf / printf

2.7 指针

• 数组名作为函数参数，相当于指针传入，引用调用
  +* (a+i) == a[i]

  • q-p == &a[i] - &a[j] 相差距离

• 指针引用 - 引用别名

2.8 结构体

• 结构体内部可以定义自身的指针

• 结构体构造函数 - 初始化序列

• 结构体定义后直接申明的变量都是调用默认构造函数 - 跟C++构造函数一样的注意点

2.9 补充

• cin / cout 只有在string输出时才调用，一般多使用printf / scanf， 因为在输出大量数据时很容易超时

• 浮点数精度

const double eps = 1e-8;
const double Pi = acos(-1.0);

# define Equ(a,b) ((fabs((a)-(b)))<(eps))   // ==
# define More(a,b) (((a)-(b))>(eps))    // > 
# define Less(a,b) (((a)-(b))<(-eps))    // < 
# define More(a,b) (((a)-(b))>(-eps))    // >= 
# define More(a,b) (((a)-(b))<(eps))    // <= 

2.10 黑盒测试

while(scanf("%d %d",&a,&b) != EOF)
while(scanf("%s",str) != EOF)
while(gets(str) != NULL)

第四章 入门篇 - 算法初步

4.1 排序

4.1.1 选择排序

• n趟枚举选出依次最小元素

void selectSort(){
    for(int i = 1;i <= n; i++){ //进行n趟操作
        int k = i;
        for (int j =i; j <= n; j++){    //选出[i,n]中最小元素，下标为k
            if(A[j] < A[k])
                k = j;
        }
        int temp = A[i];
        A[i] = A[k];
        A[k] = temp;
    }
}

4.1.2 插入排序

• 序列分为有序与无序两部分，将无序部分一一插入有序部分合适位置处，进行n-1趟

int A[maxn], n;     //n为元素个数，数组下标为1-n
void insertSort(){
    for(int i = 2; i <= n; i++){    //进行n-1趟排序
        int temp = A[i], j = i;     //temp临时存放A[i]，j从i开始往前枚举
        while(j > 1 && temp < A[j-1]){  //只要temp小于前一个元素A[j-1]
            A[j] = A[j-1];      //则把A[j-1]后移一位
            j--;
        }
        A[j] = temp;
    }
}

4.1.3 排序题与sort函数应用

• 通常做题需要排序时直接调用C++的sort函数即可

  • C中的qsort涉及许多复杂指针操作

  • 规避了经典快排极端情况会出现O(n2)

• sort(首元素地址，尾元素地址的后一个地址 [，cmp比较函数] )

  • #include

  • using namespace std;

  • sort函数会原地修改传入序列

int a[6] = {5,6,4,1,3,2}
sort(a,a+4) //将a[0]~a[3]进行排序
sort(a,a+6) //将a[0]~a[5]进行排序

• 对非可比类型，比如类，结构体等，需要实现cmp比较函数

  • STL标准容器里vector，string，deque是可用sort的，而set，map本身有序（由红黑树实现不需排序）

  • 不填cmp参数，则默认对可比较类型进行从小到大排序

bool cmp(int a, int b){     // 实现int类型从大到小排序
    return a>b;     // 返回结果为True时，a在b前排序；否则b在a前排序
}

struct node {
    int x,y;
}ssd[10];

bool cmp(node a, node b){   //实现对结构体的排序
    return a.x > b.x    // True则ab，false则ba  - 一级排序
}
bool cmp(node a, node b){   // 二级排序
    if(a.x != b.x)  return a.x > b.x;   //x不等时按x从大到小排序
    else return a.y < b.y;  //x相等时按y从小到大排序
}

• 排序题sort应用与相关Tricks

  • 按string字典序大小排序：使用strcmp(s1,s2) - 返回值>0或<0

  • 并列排名，eg. 1、2、2、4：

    • 直接设置一个变量记录或定义结构体时将排名项加入结构体中；

    • 之后先排序，后修改结构体内的排名值：a[0]=1，遍历剩余元素，若分数等于上个元素分数，则排名值相同，否则等于下标+1

// strcmp(s1,s2)应用
bool cmp(student a, student b){
    if(a.score != b.score)  return a.score > b.score;
    else return strcmp(a.name, b.name) < 0;     //名字字典序小的在前
}

// 并列排名问题 1 - 需要存储
stu[0] = 1;     //有序数组
for(int i = 1; i0 && stu[i].score != stu[i-1].score )
        r = i+1;
    //  输出信息 or stu[i].rank = r;
}

4.2 散列

4.2.1 散列定义与整数散列

• 常见散列函数：直接定址法（恒等变换&线性变换） 平方取中法 除留余数法（mod常为素数）

  • 哈希冲突：开放定址法（线性探查&平方探查） 拉链法

  • map（C++11中unordered_map）

4.2.2 字符串hash初步

• 非整数key映射整数value（初步暂时不讨论冲突，只讨论转化成唯一的整数）
  • 二维坐标点映射整数（0
• 字符串hash

  • 字符串由A~Z构成 - 将其看成26进制，转换成十进制整数映射：26^len-1 最大表示整数

  • 若有A~Za~z构成 - 则将其看成52进制，处理方法与上一致

  • 若出现数字，则有两种处理方法：

    • ① 与上一样，化为62进制

    • ② 若是只出现在特定位置，比如最后一位，则可以用拼接的方式：将前面的字母映射为十进制，拼接上后续数字

// A~Z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        id = id * 26 + (S[i]-'A')
    }
    return id;
}

// A~Za~z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        if(S[i]<='Z' && S[i]>='A')      // Z~a之间在ascll上不是相连的
            id = id * 52 + (S[i]-'A');
       else if(S[i]<='z' && S[i]>='a')
            id = id * 52 + (S[i]-'a') + 26;
    }
    return id;
}

// 假设A~Z且最后一位是数字
// A~Z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        id = id * 26 + (S[i]-'A');
    }
    id = id*10 + (S[i]-'0');
    return id;
}

4.3 递归

• 分治 & 递归

• 递归式 & 递归边界

4.4 贪心

• 简单贪心：当前局部最优来获得全局最优 - 贪心的证明思路一般使用反证+数学归纳法，证明比想到更难，若是想到时自己暂时也无法举出反例，则一般来说是正确的

• 区间贪心：

  • 区间不相交问题：给出N个开区间，选择尽可能多的开区间，使得两两之间没有重合。 - 贪心策略：先按左端点大小排序（右端点大小），总是选择最大左端点（最小右端点）

  • 区间最小点：给出N个开区间，选择最少的点，使得各区间都有点分布 - 与上述贪心策略相反，就是区间相交问题

  • 贪心解决最优化问题 - 思想希望由局部最优求解全局最优 - 适用问题需具有最优子结构性（即一个问题最优解能由其子结构最优解求得） - 贪心解决问题范围有局限性

#include 
#include 
using namespace std;
const int maxn = 110;
struck Inteval {
    int x,y;    // 开区间左右端点
} I[maxn];

bool cmp(Inteval a, Inteval b){
    if(a.x != b.x) return a.x > b.x;
    else return a.y < b.y;
}

int main(){
    int n;
    while(scanf("%d", &n), n != 0){
        for(int i = 0; i

4.5 二分

4.5.1 二分查找（整数二分）

• 基于有序序列查找算法，查找第一满足条件的位置，时间复杂度O(logⁿ)

  • mid = left+(right-left)/2（避免int越界），[left,mid-1]，[mid+1,right]；

  • 临界条件：1、查找到 2、left>right

  • 二分条件：1、循环left，相等时就是需要的值直接返回即可 2、二分初始区间为[0,n]

  • ①：序列中是否存在满足条件的元素 ②：寻找有序序列第一个满足某条件元素位置

// 序列中是否存在满足条件的元素 
int binarySearch(int A[], int left, int right, int x){
    int mid;    // mid为left和right中点
    while(left <= right){
        mid = left+ (right - left) / 2;
        if(A[mid] == x) return mid;
        else if(A[mid] > x)
            right = mid - 1;
        else left = mid + 1;
    }
    return -1;
}

// 寻找有序序列第一个满足某条件元素位置
int solve(int left, int right){     //左闭右闭写法
    int mid;
    while(left < right){        // 若左开右闭，则 left+1

4.5.2 二分法拓展

• ① 二分法 - 罗尔定理求方程根 eg.f(x)=x²-2=0 求在[left,right]范围方程根

• ② 二分答案：二分法查找结果

  • eg. 给N根木棒，切割希望得到至少K段长度相等的木棒，请问切割最长长度是多少。（切分长度越长，得到的段数越少 - 线性有序）

  • 相当于问：一个有序序列中，满足k>=K的最后一个元素位置 - 满足k

4.5.3 快速幂

• 求幂朴素做法 O(n)：aⁿ=a * a * a..... 一共进行n次乘法

• 快速幂基于二分思想，亦称二分幂，即将幂部分/2拆分，如此只需要进行logⁿ次乘法 O(logⁿ)
  • 递归写法：n/2每次

    • if n = 奇数：aⁿ = a * aa^n-1

    • if n = 偶数：aⁿ = a^n/2 * a^n/2

    • 为了加快运算，奇偶判断使用位运算：if(n&1)

  • 迭代写法：将n化为二进制，二进制第i位上有数，化为a^2i-1

    • eg. a¹¹ = a²³ * a²¹ * a²⁰

    • 步骤①：n&1判断二进制末尾是否=1，ans是则乘以a

    • 步骤②：a=a²，n>>=1，只要n大于0，则继续步骤①；结果ans返回

// 快速幂递归写法
typedef long long LL;
LL binaryPow(LL a, LL b){
    if(b == 0) return 1;
    if(b & 1) return a * binaryPow(a,b-1);
    else{
        LL mul = binaryPow(a,b/2)     // 不能同时调用两个binaryPow，时间复杂度指数倍
        return mul * mul;
    }
}

// 快速幂迭代写法
LL binaryPow(LL a, LL b){
    LL ans = 1;
    while(b > 0){
        if(b & 1)
            ans = ans * a;
        a = a* a;
        b >>= 1;
    }
    return ans;
}

4.6 two pointers

4.6.1 what's two pointers

• two pointers 思想：

  • 针对问题本身与序列特性（如有序性等），设置i，j两下标进行扫描（两端反向扫描，同端同向扫描）来降低复杂度

  • eg. partition过程，有序序列找a+b=n，归并排序的有序序列整合过程

4.6.2 归并排序

• 2-路归并排序
  • 核心：two pointers - 外排merge过程

• 递归过程：反复将当前区间[left,right]分成两半，对两个子区间[left,mid]，[mid+1,right]分别递归进行归并排序，然后边界条件为left=right；

• 非递归过程：步长为2的幂次，初始化=2，将每step个元素作为一组，内部进行排序，然后再将step✖2，重复操作。边界条件是step/2>n （方便代码，设数组下标=1开始）

// 归排递归

const int maxn = 100;
void merge(int A[], int L1, int R1, int L2, int R2){ //外排 两个有序数组合并成一个有序数组
    int i = L1, j = L2;
    int temp[maxn], index = 0;
    while(i <= R1 && j<= R2){
        if(A[i] <= A[j])
            temp[index++] = A[i++];
        else temp[index++] = A[j++];
    }
    while(i <= R1) temp[index++] = A[i++];  // 12389  23
    while(j <= R2) temp[index++] = A[j++];
    for(i = 0; i

4.6.3 快速排序

• 平均时间复杂度O(nlogⁿ)

• ① 调整序列中元素，使当前序列最左端的元素在调整后满足左侧所有元素均不超过该元素，右侧所有元素均大于该元素 - partition / two pointers过程

• ② 对该元素左侧 / 右侧分别递归进行①的调整，直到当前调整区间的长度不超过1

• 最坏时间复杂度是O(n²)，但对任意输入数据的期望时间复杂度都是O(nlogⁿ)，所以不存在一组特定的数据使这个算法出现最坏情况（算法导论证明）- 随机快排，主元随机选取

• C语言生成随机数

#include
#include
#Include
int main(){
    srand((unsigned)time(NULL));    //main开头加上
    
    printf("%d",rand());    //rand()调用生成一个随机数：[0,RAND_MAX] 自定义范围：%+-*/
}

• 随机快排 = 选取随机主元 + 经典快排

// 经典快排
void quickSort(int A[], int left, int right){
    if(left < right){
        int pos = Partition(A,left,right);
        quickSort(A,left,pos-1);
        quickSort(A,pos+1,right);
    }
}

// 随机快排
int randPartition(int A[],int left, int right){
    // 生成随机数
    int p = round(1.0*rand() / RAND_MAX * (right-left) + left);
    swap(A[p],A[left]);
    
    //partition过程
    int temp = A[left];
    while(left < right){
        while(left < right && A[right] > temp) right--;
        A[left] = A[right];
        while(left < right) && A[left] <= temp) left++;
        A[right] = A[left];
    }
    A[left] = temp;
    return left;
}

4.7 其他高效技巧与算法

4.7.1 打表

• 空间换时间，一次性将可能用到结果事先求出，需要时查表；eg. 素数表求素数查表。常见打表用法：
  1. 在程序中一次性计算出所有需要用到结果，之后查表查询
     • eg. 查询大量Fibonacci数F(n)问题，预处理将所有Fibonacci存表。 - O(nQ)降O(n+Q)
  2. 当暂无思路，用暴力方法在本地运算，输出结果保存表中，再在线上根据输入查表得结果

4.7.2 活用递推

• eg. 当序列中每一位所需要计算得值都可以通过该位左右两侧结果计算得到 / 分为左右两边计算，那么就可以通过递推进行预处理得到。

• 例题：APPAPT字符串中有两个单词"PAT"。假设字符串只由P，A，T构成，现给定字符串，问一共能形成多少个"PAT"
  • 思路：遍历数组，对每一个A，看左边有多少P，右边有多少T，然后P * T得到结果，累加所有的A结果值即可
    • 用一个leftNum来存储对应位左边的P个数，rightNum来存储对应位右边的T个数：利用递归，最左边的leftNum=0，leftNum[i] = leftNum[i-1] + (if(Array[i]是不是P))；rightNum同理计算可得。时间复杂度O(n)

#include
#include
const int MAXN = 100010;
const int MOD = 100000007;      // 要求输出结果对MOD取余
char str[MAXN];
int leftNumP[MAXN] = {0};
int main(){
    gets(str);
    int len = strlen(str);
    for(int i = 0; i< len; i++){
        if(i>0)
            leftNumP[i] = leftNumP[i - 1];
        if(str[i] == 'P')
            leftNumP[i]+=;
    }
    int ans = 0,rightNumT = 0;
    for(int i =len - ;i >= 0; i--){
        if(str[i] == 'T')   rightNumT++;
        else if(str[i] == 'A') ans = (ans +leftNumP[i] * rightNumT) % MOD;
    }
    
    printf("%d",ans);
    return 0;
}

4.7.3 随机选择算法

• 将集合划分成两部分左右区间：不要求区间内有序但要求的是区间内元素个数（但要考虑左边都比右边小的特性）

  • 思想类似于随机快排，一次随机partition后，主元左侧个数是确定的，右侧亦然。

  • eg. 求数组中第K大的数：正常想法是排序后取值，时间复杂度O(nlogⁿ)。若用随机选择算法，则是对数组进行随机partition，直至主元左区间元素个数为K-1，则此时主元就是第K大的数，时间复杂度O(n)

第五章 入门篇(3) - 数学问题

5.2 最大公约数与最小公倍数

5.2.1 最大公约数

• 欧几里得算法求最大公约数，设gcd(a,b)为a，b之间的最大公约数。

  • 设a，b均为正整数，a>b，则gcd(a,b) = gcd(b,a%b)

  • 递归边界：gcd(a,0)=a，n%1=0

// 直观写法
int gcd(int a, int b){
    if(b == 0) return a;
    else return gcd(b, a%b);    
}

// 简明写法
int gcd(int a, int b){
    return !b ? a : gcd(b, a%b);
}

5.2.2 最小公倍数

• 最小公倍数是可在最大公约数基础上求得

• 最小公倍数 = a * b / gcd(a,b)
  • 防止溢出：a / gcd(a,b) * b

5.3 分数的四则运算

5.3.1 分数的表示和化简

• 分数的表示

  • 结构体假分数形式，up分子，down分母

  • 规定

    • ① 负号放在分子上，分母恒正

    • ② 分数为0，则分子为0，分母为1

    • ③ 分子和分母最简，无1外其他公约数

• 分数的化简 - 写个函数专门处理化简，使分数格式符合规定

  • ① 当四则运算使分母为负时，分子分母取相反数

  • ② 当分子为0时，分母赋值为1

  • ③ 约分：分子分母同时除以非1最大公约数

5.3.2 分数的四则运算

• 分数的加法：（其他运算同此）

  • \(result = \frac{f1.up * f2.down + f2.up * f1.down}{f1.down * f2.down}\)

  • result.up = 分子 / result.down = 分母 - 计算结果再调用化简函数

• 进行除非时需要检查f2.up != 0 - result分母非零

5.3.3 分数的输出

• ① 输出分数前调用化简函数

• ② 如果分母down为1，则分数为整数，直接输出分子

• ③ 如果分子绝对值大于分母，则为假分数；
  • 整数 = r.up/r.down ； 分子 = r.up%r.down

• 除此以外说明为分数，按原样输出即可 - 为了防止溢出，分子分母一般为longlong

struct Fraction{    
    long long up,down;
}

Fraction reduction(Fraction result){ //化简函数
    if(result.down < 0){
        result.up = -result.up;
        result.down = -result.down;
    }
    if(result.up == 0)
        result.down = 1;
   esle {
        int d = gcd(abs(result.up),abs(result.down));
        result.up /= d;
        result.down /= d;
    }
    return result;
}

Fraction add(Fraction f1, Fraction f2){  //加法
    Fraction result;
        result.up = f1.up * f2.down + f2.up * f1.down;
        result.down = f1.down * f2.down;
        return reduction(result);
}

void showResult(Fraction r){
    r = reduction(r);
    if(r.down == 1) printf("%d",r.up);
    else if(abs(r.up) > r.down)
        printf("%d %d %d",r.up / r.down , abs(r.up) % r.down, r.down);
    else printf("%d / %d",r.up , r.down);
}

5.4 素数

• ① 如何判断给定正整数n是否是质数 ② 较短时间内得到1~n素数表

5.4.1 素数的判断

• O(n)：n求余2~n-1为0则非素数

• O(sqrtN)：k * (n/k) = n，n若非素数，至少也有两个约数，则一定满足一个大于一个小于sqrt(n) - 所以只要判断2~[sqrt(n)]（向下取整）余数非0
  • 两种写法，一种是sqrt(n)求出并用变量存储，另一种是直接i * i作为循环结束条件；前者安全，后者当n接近int范围上界时可能导致i * i溢出 - 解决办法就是将i改为longlong

bool isPrime(int n){    //sqrt(n)
    if(n <= 1) return false;
    int sqr = (int)sqrt(1.0*n);
    for(int i =2; i<=sqr; i++){
        if(n%i == 0) return false;
    }
    return true;
}

bool isPrime(int n){    // i * i
    if(n <= 1) return false;
    for(long long i = 2; i * i <= n; i++)
        if(n % i == 0) return false;
    return true;
}

5.4.2 素数表的获取

• O(n * sqrt(n))：遍历1~n，每个都调用O(sqrt(n))判断是否是素数，再打印；当n超过10⁵时效率较低

• O(nlog^logn)：Eratosthenes筛法（埃式筛法）
  • 思想：重点是筛。

    • 2~n-1序列，标记数组全为true，从2开始，先删去2和所有2的倍数（即令标记数组为false）；

    • 再到3，判断标记数组是否是true，删去3和所有3的倍数；

    • 再到4，判断false跳过，再到5，直至结束遍历
• O(n)：欧拉筛法（线性筛）

  • 思想：在埃式筛法的基础上，不重复设置标记，每个合数只被其最小质因子筛选一次

  • eg. 30只会被2筛选，不会被3、5等筛选，

    • 2~n-1序列，标记数组全为true，从2开始，判断标记数组true，2加入素数数组，2 * 2置为合数

    • 再到3，判断true，加入素数数组，2 * 3，3 * 3置为合数；

    • 再到4，判断false，2 * 4置为合数，退出；

  • 最重要的一步：if(i % prime[j] == 0) break; - 此时退出因为后续j+1的vis[i*prime[j+1]]对prime[j+1]而言它不是最小质因数，prime[j]是，后面其他质数更不是，所以直接退出遍历下一个

// O(n * sqrt(n))
const int maxn = 101;
int prime[maxn], pNum = 0;
bool p[maxn] = {0};
void Find_Prime(){
    for(int i =1; i < maxn; i++){
        if(isPrime(i) == true){
            prime[pNum++] = i;
            p[i] = true;
        }
    }
}

// 埃式筛法
void Find_Prime(){
    for(int i =2; i < maxn; i++){
        if(p[i] == false){
            prime[pNum++] = i;
            for(int j = i+i; j

5.5 质因子分解

• eg. 20 = 2 * 2 * 5

• 用结构体数组存储十种素数 - 2 * 3 * 5...前十个素数乘积已经超过int范围，故factor数组开十个即可
  • fac[0].x = value ; fac[0].cnt = times;
• 思路 - O(sqrt(n))

  • n的质因子要么全部都小于sqrt(n)；要么只有一个大于sqrt(n)，其余均小于sqrt(n)

  • ① 遍历 2~sqrt(n)中的素数，n对素数求余，若是为0，则初始化质因子，并循环除确定其个数

  • ② 遍历完成后若n仍然大于1，则剩下的n就是大于sqrt(n)的质因子，初始化并加入factor数组即可

5.6 大整数运算

5.6.1 大整数存储

• 用int数组对大整数各位存储，高位存储高位，低位存储低位，方便遍历运算；读入数组后需要进行数组逆转
  • 比较大小：先比较位数len，再从最高位往低位比较

// 初始化
struct bign{
    int d[1000];
    int len;
    bign(){
        memset(d,0,sizeof(d));
        len = 0;
    }
}

// 读入数组
bign change(char str[]){
    bign a;
    a.len = strlen(str);
    for(int i = 0; i < a.len; i++)
        a.d[i] = str[a.len-i-1] - '0';
    return a;
}

// int compare(bign a, bign b){
    if(a.len > b.len) return 1;
    else if(a.len < b.len) return -1;
    else{
        for(int i = a.len - 1; i >= 0; i--){
            if(a.d[i] > b.d[i]) return 1;
            else if(a.d[i] < b.d[i]) return -1;
        }
    }
    return 0;
}

5.6.2 大整数的四则运算

• 加法：跟正常加法一样，个位+个位+进位

• 减法：个位 - 个位 - 借位

• 乘法：int * big 各位相乘；big * big 同上加法

• 除法：从高到低逐位相除

5.7 扩展欧几里得算法（略）

• 扩展欧几里得算法（ax + by = gcd(a,b)的求解）

• 方程ax + by = c的求解

• 同余式 ax = c(mod m)的求解

• 逆元的求解以及(b/a)%m的计算

5.8 组合数

5.8.1 关于n!的一个问题

• 求n!中有多少个质因子p - 6!中有4个质因子2
  • O(nlogⁿ)：将1~n每个数遍历各有多少个质因子p再叠加
    • 遍历数i循环除以p
  • O(logⁿ)：n!中有(n/p + n/(p2) + n/(p3) + ...)个质因子p，其中除法均为向下整除

    • 延申：n!的末尾有多少个零：等于n!中质因子5的个数

    • 推广：n!中质因子p的个数 = 1~n中p的倍数个数(n/p)加上((n/p)!)中质因子p的个数 - 递归版本求质因子p个数

//  O(nlogn)
int cal(int n ,int p){
    int ans = 0;
    for(int i = 2; i <= n; i++){
        int temp = i;
        while(temp % p == 0){
            ans++;
            temp /= p;
        }
    }
    return ans;
}

// O(logn) 非递归版本
int cal(int n , int p){
    int ans = 0;
    while(n){
        ans += n / p;
        n /= p;
    }
    return ans;
}

// O(logn) 递归版本
int cal(int n, int p){
    if(n

5.8.2 组合数的计算

• 组合数C_n^m：从n个不同元素中选出m个元素的选法，不考虑位置

  • C(n,m) = n! / m!(n-m)!

  • C_n^m = C_n^n-m

  • C_n⁰ = C_nⁿ = 1

• ① 如何计算C_n^m

  • 方法一：通过三个阶乘的定义式计算 - n! / m!(n-m)! 即使用longlong也只能n<=21

  • 方法二：通过递推公式计算 - C_n^m = C_n-1^m + C_n-1^m-1

    • 边界条件就是让n和m一样大；或者让m变为0

    • 重复计算问题：开一个二维数组存储已经计算过的值即可

    • 递归写法计算单个C(n,m)小于O(n²) 与 非递归写法(递推写法)计算所有C(n,m)复杂度O(n²)

  • 方式三：通过定义式的变形来计算

    • \(C_{n}^{m} = \frac{n!}{m! * (n-m)!} = \frac{(n-m+1) * (n-m+2) * ... * (n-m+m)}{1 * 2 * 3 ... * m}\)

    • \(\frac{(n-m+1) * (n-m+2) * ... * (n-m+m)}{1 * 2 * 3 ... * m} = \frac{\frac{\frac{n-m+1}{1} * (n-m+2)}{2}* (n-m+2)}{3}...\)

    • (n-m+1) * (n-m+2)... * (n-m+i) / (1 * 2 ... * i) = C_n-m+iⁱ一定是个整数；所以上述变形式就可以保证不会在边乘边除的过程中出现小数导致误差的情况 - 由于除法故保证避免了溢出问题，n<=62左右，时间复杂度O(m)

// 方法一
long long C(long long n, long long m){
    long long ans = 1;
    for(long long o = 1; i <= n; i++)
        ans *= 1;
    for(longlong i = 1; i <= m; I++)
        ans /= i;
    for(long long o = 1; i <= n - m; i++)
        ans /= i ;
    return ans;
}

// 方式二 - 递归
long long res[67][67] = {0};
long long C(long long n, long long m){
    if(m == 0 || m == n) return 1;
    if(res[n][m] != 0) return res[n][m];
    return res[n][m] = C(n-1,m) + C(n-1,m-1);
}

// 方式二 - 递推
const int n = 60;
void calC(){
    for(int i = 0; i <= n; i++)
        res[i][0] = res[i][i] =1;
    for(int i = 2; i <= n; i++)
        for(int j = 0; j <= i/2; j++)}
            res[i][j] = res[i-1][j] +res[i-1][j-1];
            res[i][j-1] = res[i][j] ;
        }
}

// 方法三
long long C(long long n, long long m){
    long long ans = 1;
    for(long long i = 1; i<=m; i++)
        ans =ans * (n-m+i) / i;
    return ans;
}

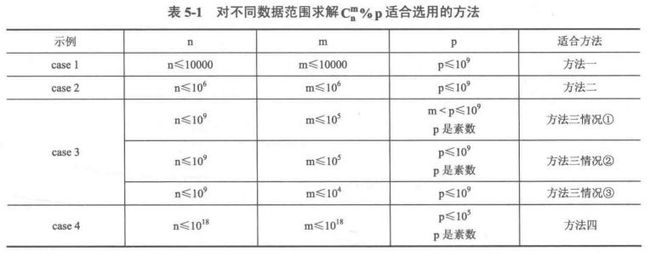
• ② 如何计算C_n^m%p
  • 方法一：通过递推公式计算，基于第一问的方法二，只需要在原代码上对p取模即可
    • 也是分成递归与递推两种代码实现
  • 方法二：根据定义式计算 - 将组合数C_n^m进行质因子分解，计算每一组质因子p_i^cut%p相乘再取模即可 - 利用5.8.1中的方法对n!，m!，(n-m)!分别计算含质因子p的个数x,y,z，C_n^m中的质因子个数为x-y-z。
    • 时间复杂度O(klogⁿ)，其中k不超过n的质数个数

  • 方法三：通过定义式的变形计算（略）

  • 方法四：Lucas定理(卢卡斯)（略）

// 方法一 - 递归
int res[1010][1010] = {0};
int C(int n, int m, int p){
    if(m == 0 || m == n) return 1;
    if(res[n][m] != 0) retirm res[n][m];
    return res[n][m] = (C(n-1,m) + C(n-1,m-1)) % p;
}

// 方法一 - 递推
void calC(){
    for(int i =0; i <= n; i++)
        res[i][0] = res[i][i] =1;
    for(int i =2; i <= n; i++)
        for(int j = 0; j <= i / 2; j++){
            res[i][j] = (res[i-1][j] + res[i-1][j-1]) % p;
            res[i][i-j] = res[i][j];
        }
}

// 方法二
int prime[maxn];

int C(int n ,int m ,int p){
    int ans = 1;
    for(int i = 0; prime[i] <= n; i++){
        int c = cal(n,prime[i]) - cal(m,prime[i]) - cal(n-m,prime[i]);
        ans = ans * binaryPow(prime[i],c,p) % p;
    }
    return ans;
}

//方法四
int Lucas(int n ,int m){
    if(m == 0) return 1;
    return C(n % p,m % p) * Lucas(n / p, m / p) % p;
}

第六章 C++标准模板库(STL)

6.1 vector的常见用法详解

未完待续