A*算法是对Best-First算法的一种改进,核心思想是广搜,利用open表和close表对节点进行剪枝,同时利用启发式测度来选择最优的扩展节点。
A*算法在满足一定条件下找到的解必然是最优解。
最短路得到最优解条件:A*算法的启发式函数h如果小于等于真实值n的话,那么算法是能得到最优解的,若h大于等于真实值n,那么就不能保证得到最优解。
主要数据结构:
opened_table:采用优先队列实现的小顶堆,用于存放待扩展结点,同时利用F值作为排序指标;
closed_table:采用set(红黑树)实现,便于快速查找格是否存在于closed_table中;
启发式函数:采用曼哈顿距离作为启发式函数,即当前节点与终点的水平、竖直相差方格的数目之和;
问题描述:
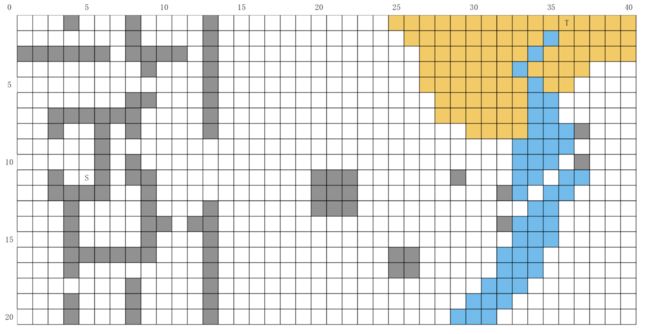
精灵王子Haposola一大早从城堡中起床,要去沙漠中河流消失的地方寻找失落的宝藏。长路漫漫,处处险恶,精灵王子要尽快到达目标地点。以下图为输入,寻找地图上给出的起点和终点间的最小代价路径。规则和条件如下。
(1) 每一步都落在方格中,而不是横竖线的交叉点。
(2) 灰色格子表示障碍,无法通行。
(3) 在每个格子处,若无障碍,下一步可以达到八个相邻的格子,并且只可以到达无障碍的相邻格子。其中,向上、下、左、右四个方向移动的代价为1,向四个斜角方向移动的代价为√2。
(4) 在一些特殊格子上行走要花费额外的地形代价。比如,黄色格子代表沙漠, 经过它的代价为4;蓝色格子代表溪流,经过它的代价为2;白色格子为普通地形,经过它的代价为0。
(5) 经过一条路径总的代价为移动代价+地形代价。其中移动代价是路径上所做的所有移动的代价的总和;地形代价为路径上除起点外所有格子的地形代价的总和。
启发式函数:
H = G * 5 + F
其中G代表已走过的真实距离;F代表当前点到目标点的曼哈顿距离;
为什么要给G乘上5?
因为任务的要求是要走过路程最短,因此我们的启发式测度更加的看重实际走过的距离,而不是通过曼哈顿距离估计的路程。
所以给G赋予更大的权值,保证我们得到的解是最优解,即最短路程。【就是一个加权的思路】
地图处理:
值得一提的是,由于我们的地图是图片的形式给出的,那么我们需要将图片转化为数组读入程序。此处借助Python的第三方库PIL实现地图输入的采样、以及实验结果的生成。
通过均匀采样将地图图片输入转化为字符数组的函数。
同时对于预测得到的路径,我们也需要根据我们的结果,再生成结果地图,详见代码。
算法步骤:
1. 首先将给定图2输入程序;
2. 通过均匀采样,将其转化为字符数组,y代表沙漠,g代表障碍,w代表普通道路,b代表溪流;
3. 输入起点和终点,同时将起点、终点、字符数组存储的地图输入算法;
4. 把起始格添加到opened表;
5. 如果开启列表不为空,重复如下的工作:
a) 寻找开启列表中F值最低的格子,作为当前格;
对于8个方向,寻找当前格的活节点:
i. 如果当前点是终点,则返回回溯的路径;
ii. 如果活节点超出地图边界,则跳过;
iii. 如果活节点位于closed表中,则跳过;
iv. 如果它不在开opened表中,则计算其F,G,H值,然后添加进opened表;
v. 如果它在opened表中,则判断opened表中格的G值是否大于当前活节点,如果大于,则说明当前活节点更优,代价更小,那么将opened表中这一格的父节点改成当前格,同时重新计算G,F值;
b) 把当前格加入closed表;
6. 将路径结果与地图生成图片,方格像素为30*30px,边界像素为1px;
主要代码:
地图方格定义:
class AreaBlock(object):
def __init__(self, father, kind, g, row, col):
self.father = father
self.kind = kind
self.coordinate_row = row
self.coordinate_col = col
self.g = g
self.f = 0.0
def get_coordinate(self):
return self.coordinate_row, self.coordinate_col
def __lt__(self, other):
"""
operator <
:param other:
:return:
"""
return self.f < other.f
地图处理:
def process_map():
"""
将图片变化为字符矩阵
:return:
"""
game_map = [[0] * 41]
im = Image.open('map.png')
pix = im.load()
width = im.size[0]
height = im.size[1]
"""
取样点坐标
"""
start_x = int(math.floor(width / 40)) - 10
x_step = int(round(width / 40))
start_y = int(math.floor(height / 20)) - 10
y_step = int(round(height / 20))
for i in range(20):
row = [0]
y = start_y + i * y_step
for j in range(40):
x = start_x + j * x_step
if pix[x, y] == GRAY:
row.append('g')
elif pix[x, y] == BLUE:
row.append('b')
elif pix[x, y] == YELLOW:
row.append('y')
elif pix[x, y] == WHITE:
row.append('w')
else:
print("error")
game_map.append(row)
return game_map
A*寻路:
def search(game_map, start_pos, end_pos):
"""
寻路算法
:param game_map:
:param start_pos:
:param end_pos:
:return:
"""
# 确定边界
max_row = len(game_map) - 1
max_col = len(game_map[0]) - 1
# 创建open表, close表
opened_table = PriorityQueue()
closed_table = set()
# 初始化open表
opened_table.put(start_pos)
while not opened_table.empty():
current_area_block = opened_table.get()
for direct in direction:
col_index = current_area_block.coordinate_col + direct[0]
row_index = current_area_block.coordinate_row + direct[1]
# 边界检测, 如果它不可通过或者已经在关闭列表中, 跳过
if (row_index, col_index) in closed_table or bound(row_index, col_index, max_row=max_row, max_col=max_col):
continue
if game_map[row_index][col_index] == 'g':
continue
# 计算移动代价
move_cost = 1
if math.fabs(direct[0]) == 1 and math.fabs(direct[1]) == 1:
move_cost *= math.sqrt(2)
# 计算地形代价
land_cost = get_cost(game_map[row_index][col_index])
# 创建block
next_area = AreaBlock(father=current_area_block,
kind=game_map[row_index][col_index],
g=current_area_block.g + move_cost + land_cost, # 地形代价 + 移动代价
row=row_index,
col=col_index)
# 如果当前节点是目标节点,则找到路径
if col_index == end_pos.coordinate_col and row_index == end_pos.coordinate_row:
# 向父节点开始回溯,输出路径
return find_path(next_area)
# 检查该点是否在open表中
result = None
tmp_queue = []
while not opened_table.empty():
tmp_block = opened_table.get()
if tmp_block.get_coordinate() == next_area.get_coordinate():
result = tmp_block
break
tmp_queue.append(tmp_block)
while len(tmp_queue) != 0:
opened_table.put(tmp_queue.pop())
opened_table.task_done()
# 检查该点是否在open表中, 如果不在则加入, 同时计算启发值 F = G + H
next_area.f = heuristic(next_area, end_pos)
if result is None:
opened_table.put(next_area)
else:
"""
用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。
"""
if next_area.g < result.g:
opened_table.put(next_area)
else:
opened_table.put(result)
closed_table.add(current_area_block.get_coordinate())
return None
采用栈实现路径的回溯:
def find_path(target_area_block):
"""
回溯寻找路径
:type target_area_block: AreaBlock
:param target_area_block:
:return:
"""
print(target_area_block.g)
# 用栈存储路径
stack = [target_area_block.get_coordinate()]
father_area_block = target_area_block.father
while father_area_block is not None:
stack.append(father_area_block.get_coordinate())
father_area_block = father_area_block.father
return stack
根据回溯的路径生成结果图片:
def save_result(game_map, path):
"""
将结果保存为图片
:param game_map:
:param path:
:return:
"""
pix = convert_array_to_pixel(game_map, path)
array = np.asarray(pix, dtype=np.uint8)
image = Image.fromarray(array, 'RGBA')
image.save("result.png")
def convert_array_to_pixel(arr, path):
"""
将字符数组转化为像素
:param arr:
:param path:
:return:
"""
width = 20
height = 20
pixels = []
for i in range(1, len(arr)):
line = []
for j in range(1, len(arr[i])):
if arr[i][j] == 'g':
line.append(GRAY)
elif arr[i][j] == 'b':
line.append(BLUE)
elif arr[i][j] == 'y':
line.append(YELLOW)
elif arr[i][j] == 'w':
line.append(WHITE)
pixels.append(line)
# 绘制路径
for point in path:
x, y = point
pixels[x - 1][y - 1] = RED
# 处理分辨率,放大
result = [[BORDER] * ((len(pixels[0])) * width + (len(pixels[0]) + 1))]
for i in range(len(pixels)):
line = [BORDER]
for j in range(len(pixels[i])):
line.extend([pixels[i][j]] * width)
line.append(BORDER)
for j in range(height):
result.append(line)
result.append([BORDER] * len(line))
del pixels
return result
实验结果:
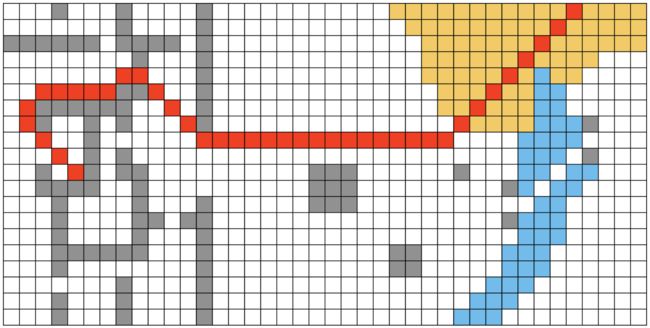
当起点为(11, 5)时,终点为(1, 36),cost=67.0416结果为(红色为路径):
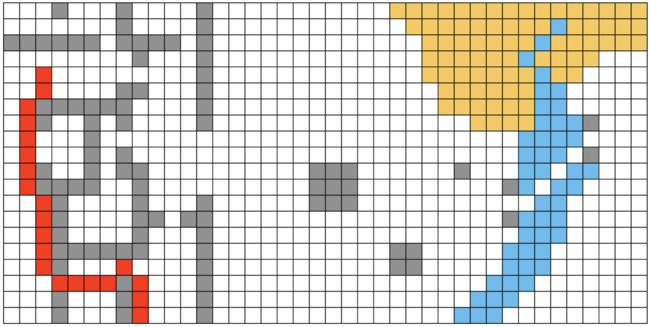
当起点为(5, 3)时,终点为(20, 9),cost=22.0711结果为(红色为路径):
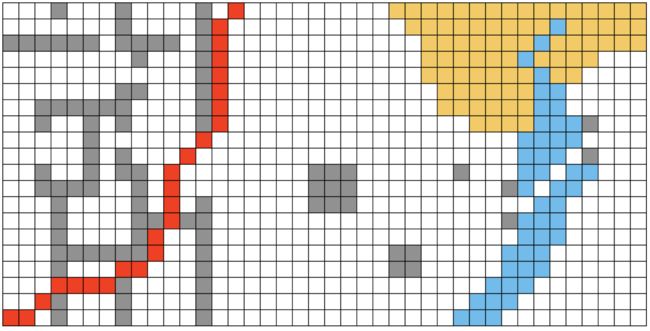
当起点为(20, 1)时,终点为(1, 15),cost=27.7279结果为(红色为路径):
总结
本次实验为了实现可视化,使用了python的第三方库Pillow,该库支持读取图片,并转化为数组的形式存储,每个点为RGBA的颜色值。考虑到给定的图片是等间隔的正方形组成,因此想到了利用等间隔采样来提取每个方格的颜色值,从而判定区域类型。
从我犯的错误中也可以总结出,A算法未必会得到最优解,只有在启发式函数满足一定条件的情况下,得到的解才满足最优解,否则只能得到可行解。由于A算法需要频繁查找活结点是否存在于closed表中,于是利用python封装好的set数据结构进行closed表的存储,set是使用红黑树实现的,因此查询速度很快;由于每次从opened表中读取的是代价最小的结点,因此采用PriorityQueue优先队列来维护一个小顶堆,每次从堆顶取得具有最小值的结点,对其进行扩展。
A算法的启发式函数得到的估计值h是不准确的,设当前区域到达目标区域的代价为n,那么h≤n,这种情况下,导致A算法搜索的区域数多,搜索范围大,效率低。同时,A*算法的启发式函数h如果小于等于真实值n的话,那么算法是能得到最优解的,若h大于等于真实值n,那么就不能保证得到最优解。
在生成路径结果的时候,考虑到了pillow的原理,读取图片-> RGBA字典 ->字符数组的流程,于是猜想通过逆过程来生成图片,首先将路径叠加到字符数组,然后再通过字符数组转为为RGBA的数组,于是来生成实验结果。
Github源码