1| 棋盘覆盖问题 |
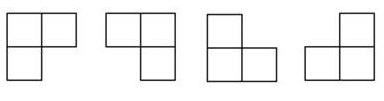
| 在一个2k x 2k ( 即:2^k x 2^k )个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
| Input |
| 输入文件第一行是一个整数T,表示有多少组测试数据,接下来是T组测试数据,共2T行,每组第一行为整数n,是2的n次幂(1<=n<=64),表示棋盘的大小为n*n,第二行是两个整数,代表特殊方格所在行号和列号。
|
| Output |
| 先输出“CASE:i,然后按样例输出。数据间用制表符隔开(‘t’),每行最后一个数据后无制表符。
|
| Sample Input |
|
2
2
0 0
8
2 2
|
| Sample Output |
|
CASE:1
0 1
1 1
CASE:2
3 3 4 4 8 8 9 9
3 2 2 4 8 7 7 9
5 2 0 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
|
| Judge Tips |
| 要求遍历顺序按从左到右,从上到下。 |
| 棋盘覆盖问题 |
| **Time Limit: **1000ms, Special Time Limit:2500ms, Memory Limit:32768KB |
| Total submit users: 62, **Accepted users: **26 |
| **Problem 10432 : *No special judgement |
| Problem description |
| 在一个2k x 2k ( 即:2^k x 2^k )个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。 [图片上传中...(image-d600f9-1520562591343-0)] |
| Input |
| 输入文件第一行是一个整数T,表示有多少组测试数据,接下来是T组测试数据,共2T行,每组第一行为整数n,是2的n次幂(1<=n<=64),表示棋盘的大小为nn,第二行是两个整数,代表特殊方格所在行号和列号。
|
| Output |
| 先输出“CASE:i,然后按样例输出。数据间用制表符隔开(‘t’),每行最后一个数据后无制表符。
|
| Sample Input |
|
2
2
0 0
8
2 2
|
| Sample Output |
|
CASE:1
0 1
1 1
CASE:2
3 3 4 4 8 8 9 9
3 2 2 4 8 7 7 9
5 2 0 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
|
| Judge Tips |
| 要求遍历顺序按从左到右,从上到下。 |
棋盘覆盖问题:
首先大致描述一下题目:
在一个2k×2k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何
k≥0,有4^k种不同的特殊棋盘.
下图–图(1)中的特殊棋盘是当k=2时16个特殊棋盘中的一个:
图(1)
题目要求在棋盘覆盖问题中,要用下图—图(2)所示的4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖.
图(2)
思路分析:
当k>0时,将2k×2k棋盘分割为4个2k-1×2k-1子棋盘,如下图–图(3)所示:
图(3)
特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格.为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处。
如下图–图(4)所示,这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而原问题转化为4个较小规模的棋盘覆盖问题.递归地使用这种分割,直至棋盘简化为1×1棋盘。
这样每个区域有一个黑点(在构造之后)的的棋盘是一定能符合题意填满的,因为最终都可以化成2*2的形状(三个白一个黑)。
抄个代码:
#include
using namespace std;
int tile=1; //L型骨牌的编号(递增)
int board[100][100]; //棋盘
/*****************************************************
* 递归方式实现棋盘覆盖算法
* 输入参数:
* tr--当前棋盘左上角的行号
* tc--当前棋盘左上角的列号
* dr--当前特殊方格所在的行号
* dc--当前特殊方格所在的列号
* size:当前棋盘的:2^k
*****************************************************/
void chessBoard ( int tr, int tc, int dr, int dc, int size )
{
if ( size==1 ) //棋盘方格大小为1,说明递归到最里层
return;
int t=tile++; //每次递增1
int s=size/2; //棋盘中间的行、列号(相等的)
//检查特殊方块是否在左上角子棋盘中
if ( dr=tc+s ) //在
chessBoard ( tr, tc+s, dr, dc, s );
else //不在,将该子棋盘左下角的方块视为特殊方块
{
board[tr+s-1][tc+s]=t;
chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
}
//检查特殊方块是否在左下角子棋盘中
if ( dr>=tr+s && dc=tr+s && dc>=tc+s ) //在
chessBoard ( tr+s, tc+s, dr, dc, s );
else //不在,将该子棋盘左上角的方块视为特殊方块
{
board[tr+s][tc+s]=t;
chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
}
}
void main()
{
int size;
cout<<"输入棋盘的size(大小必须是2的n次幂): ";
cin>>size;
int index_x,index_y;
cout<<"输入特殊方格位置的坐标: ";
cin>>index_x>>index_y;
chessBoard ( 0,0,index_x,index_y,size );
for ( int i=0; i 2 循环日程表问题;
#include
using namespace std;
int a[100][100];
void form(int size){
if(size == 1) return ;
int t = size/2;
form(t);
for(int i = 1; i <= t; i++){
for(int j = 1; j <= t ;j++){
a[i+t][j] = a[i][j] + t;
a[i+t][j+t] = a[i][j];
a[i+t-t][j+t] = a[i+t][j];
}
}
}
int main(){
int n;
scanf("%d", &n);
a[1][1]=1;
form(n);
for(int i = 1; i <= n ; i++){
for(int j = 1; j <= n ; j++){
printf("%d ", a[i][j]);
}
printf("\n");
}
return 0;
}