前言——主要内容
这篇笔记是StatQuest系列视频教程的第38小节,在此备注一下,在StatQuest系列视频中,从38小节到57小节是机器学习方面的内容。第38小节的内容是LDA,全称是Linear Discriminant Analysis,中文翻译为线性判别分析,这种方法能够对一些数据进行分类,对数据分类的其它方法还是PCA,t-SNE,SVM。
LDA简介
我们先来看一个场景。
例如,我们开发了一种抗肿瘤药物,这个药物对于某些患者的治疗效果很好,但是对某些患者则有很大的副作用。此时,我们就面临了一个问题,这些药物如何给患者吃?
对于这样的问题,一个简单的解决思路就是,我们把这两类患者(一类药物有效的患者,一类药物有副作用的患者)的基因检测一下,或许他们的基因表达能够为我们合理用药提供决策依据,如下所示:
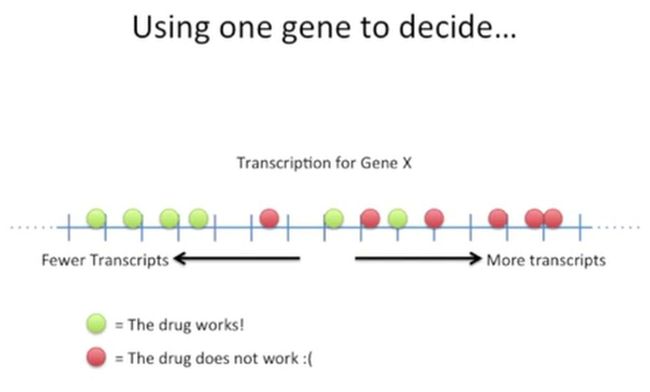
由于患者表达的基因很多,我们先从最简单的一个基因X谈起。我们以基因X的转录水平为依据,观察基因X在这两类患者体内的转录情况,如下所示:
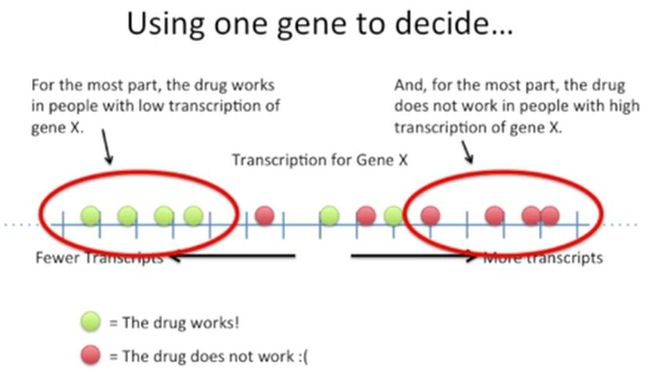
其中,绿色的点表示患者的基因X转录水平比较低,药物疗效好;红点表示患者的基因X转录水平高,药物疗效差。对于左侧的大部分患者来说,确实如此,如下所示:
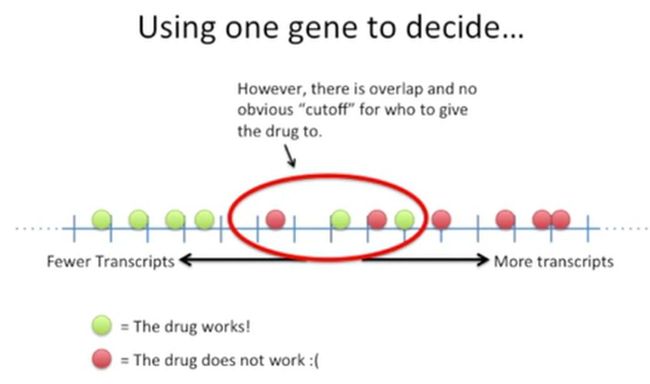
但是,让人比较纠结的是,中间这些患者,他们的基因X转录水平处于中间水平,药物效果也不明,如下所示:
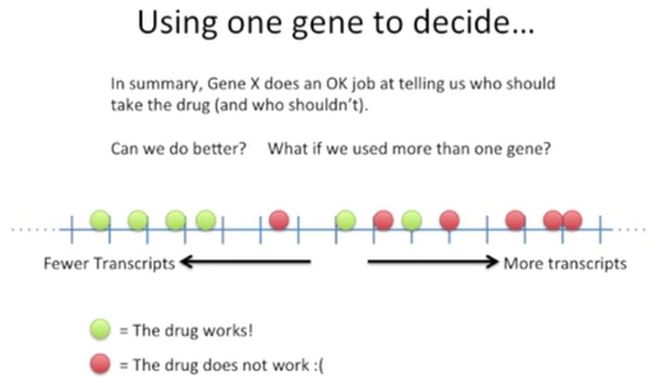
如果不考虑患者的基因X转录的中间水平,也不考虑药物对这些患者的治疗情况,总体上来说,仅基因X还是能够为我们提供一定的决策依据的,虽然它也不是特别完美。
但是,如果我们想要更好地区分哪些患者服用药物,哪些患者不服用药物,怎么办?
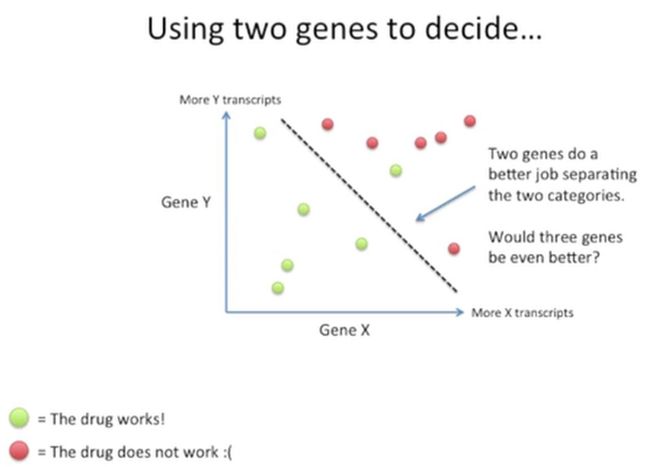
其实这个里,可以再加入一个基因,看一下两个基因能否更好地为选择患者使用药物提供依据,如下所示:
我们再找的这个基因暂且把它称为基因Y,把这两个基因放到坐标轴上,我们可以发现,用一条虚线可以比较好地把这两类患者划分开,如下所示:
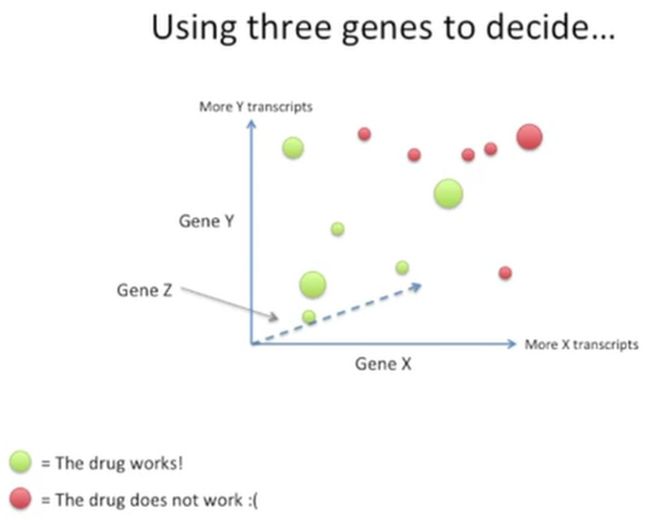
此时,我们还可以再进一步,用3个基因看一下,效果会不会更好,此时我们把这第3个基因暂且叫做基因Z,此时就变成了三维的坐标系,如下所示:
上面的这个坐标系是三维的,其中我们发现有的点大,有的点小,这个好理解,比较小的点离我们比较远,大的点离我们比较近,此时我们可以通过一个平面把这两类患者分开,如下所示:
那我们再进一步,能否用4个基因把这两类患者区分开来?如下所示:
不过问题是,我们无法直观地绘制出四维坐标,只能靠想了。如果我们学过PCA,那我们就会想到,此时我们面临的问题与PCA分析的问题比较类似(下一篇笔记会讲PCA)。
PCA主要是通过找出哪些变异最大的基因来实现降维的,当我们有多维数据时,使用PCA能够很方便地将多维数据降为三维或二维数据(例如绘制成XY散点图)。但是,我们在这个案例中,我们对哪些变异大的基因没兴趣,相反我们使用LDA时,所关注的是怎么能够最大程度地把这两类患者分开,为我们的给药提供决策依据。LDA虽然与PCA有点类似,但是LDA是对已知分类进行最大程度的区分,而PCA则是对未知分类进行降维,如下所示:
再来看一下最后一段话,它讲的是LDA与PCA的区别,如下所示:
为了更深入地理解LDA与PCA,可以搜索一些有关有监督学习和无监督学习的资料看一下。
一个简单的案例
在这个案例中,我们还是以前面的案例为基础,将2维的坐标(X基因与Y基因构成的坐标)降为1维的坐标,如下所示:
那么此时问题来了,我们怎么去降维?
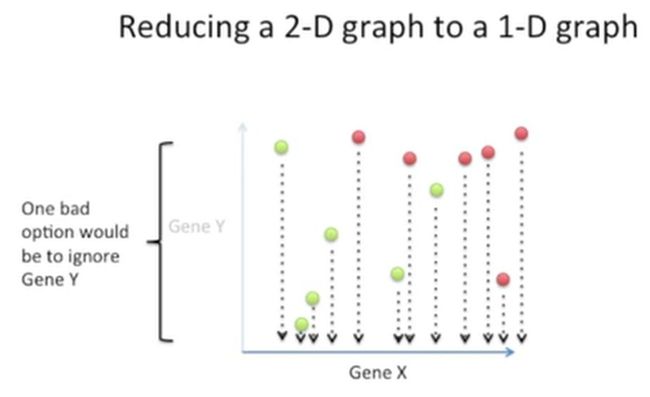
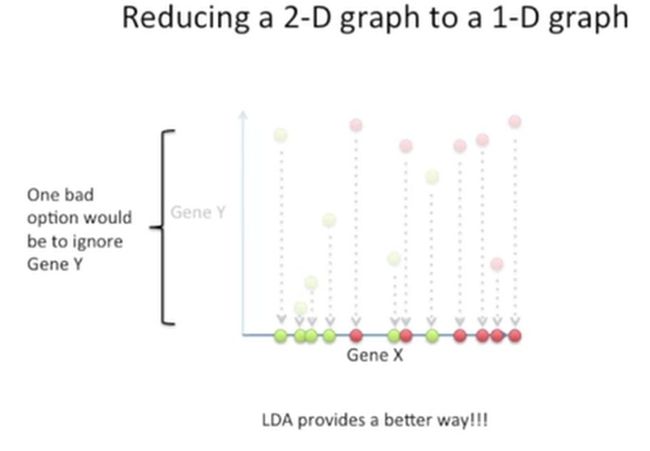
首先,看一个简单粗暴的降维方法,我们不要基因Y,只要基因X,直接把它们投射到X轴上,这就像有一个压力,从上到下,直接把Y轴拍扁一样,如下所示:
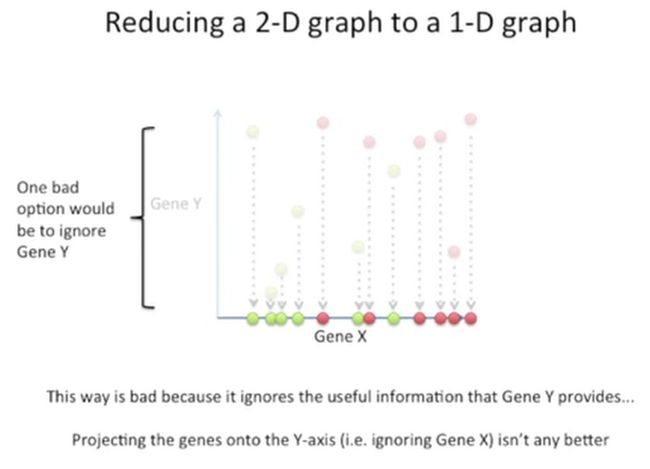
这种方法非常粗糙,它无法区分出这两类患者,因为它忽略了基因Y提供的有用信息,如果我们忽略基因X,把所有的点投射到Y轴,也是如此,如下所示:
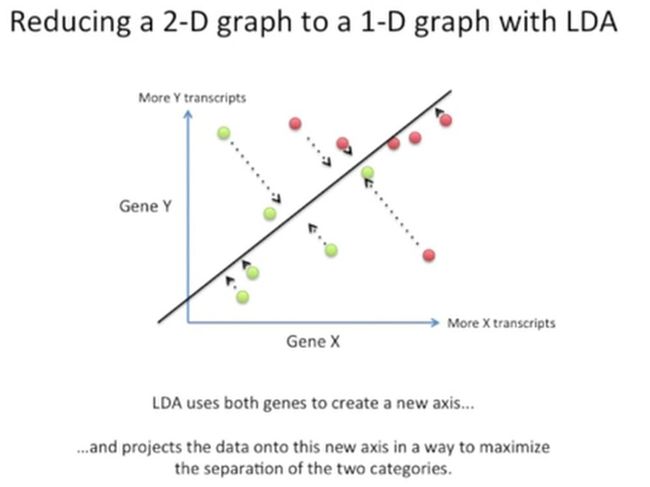
此时,我们就可以使用LDA这种方法,把二维坐标降为一维坐标的同时,还能同时保留基因Y与基因X的信息,如下所示:
LDA会计算出一个新的坐标轴,然后将所有的点都投射到这个新的坐标轴上去,并能够很好地把这两类患者进行区分,如下所示:
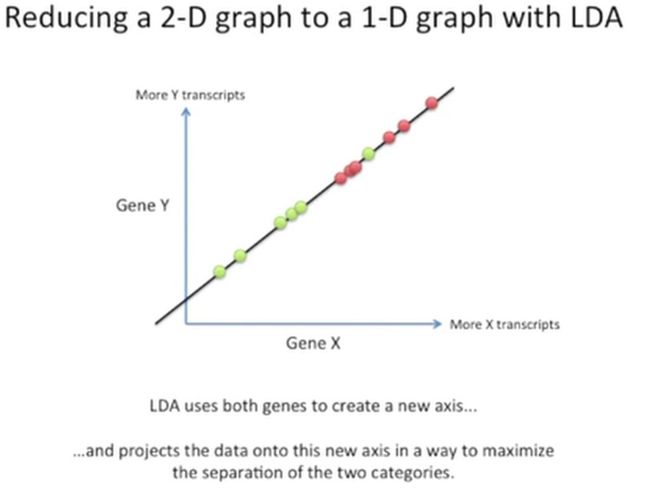
结果就是像这样:
此时又有问题了,LDA是如何做到的?
LDA的原理
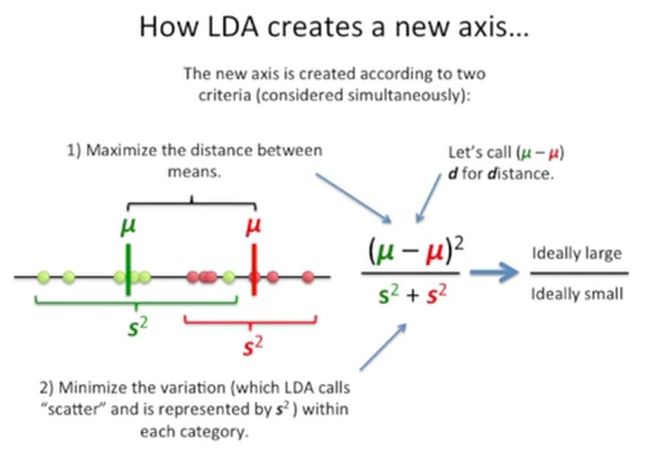
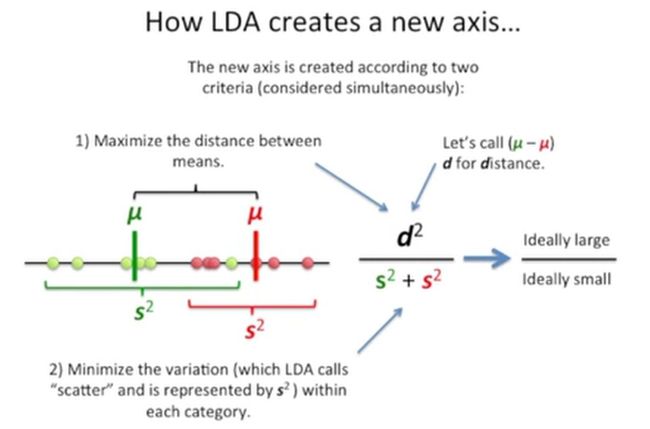
LDA生成的这个新坐标轴要同时满足两个标准:
第一,两类患者的均值要足够远(也就是下图中分子要尽量大);
第二,两类患者的变异要小(下图中分母尽量小),如下所示:
通常,我们会将两个分类的均值差的平方称为d,如下所示:
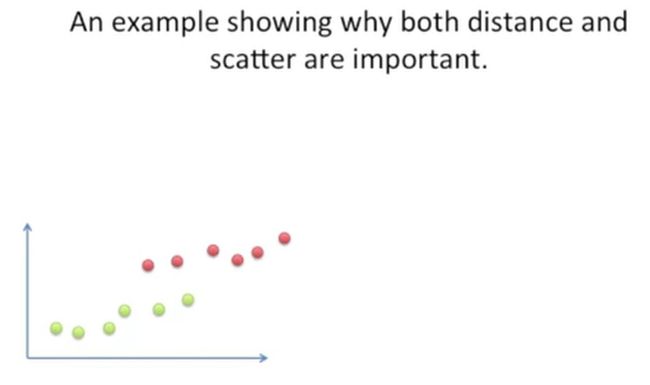
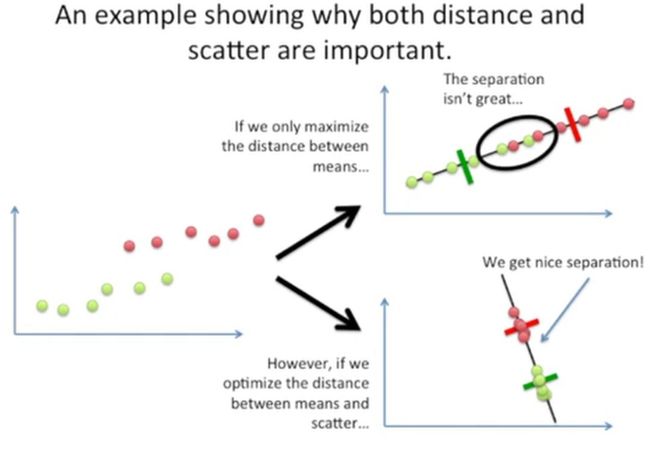
再看一个案例,这个案例主要用于说明两个分类的均值距离与散点(就是标准差)的重要性,如下所示:
在上面的这个案例中,我们发现,从x轴的角度来看,这两类数据有部分重合,如果我们只考虑这两类数据均值之间的距离的话,当这个距离最大时,那么新生成的坐标轴就像下图中右上的角的样子,它的区分度不太好,中间有两个数据是重叠的,如果我们即考虑均值距离又考虑数据点的离散程度,那么我们新生成的坐标轴,让这两类数据投射到上去,就会得到很好的区分,如下图右图下的样子:
如果我们有超过2个基因(也就是超过2维的数据)时,处理这些数据的方法还是相同的,创建的新坐标轴要使得这两类数据的均值距离最大,同时使数据点的离散程度最小,如下所示:
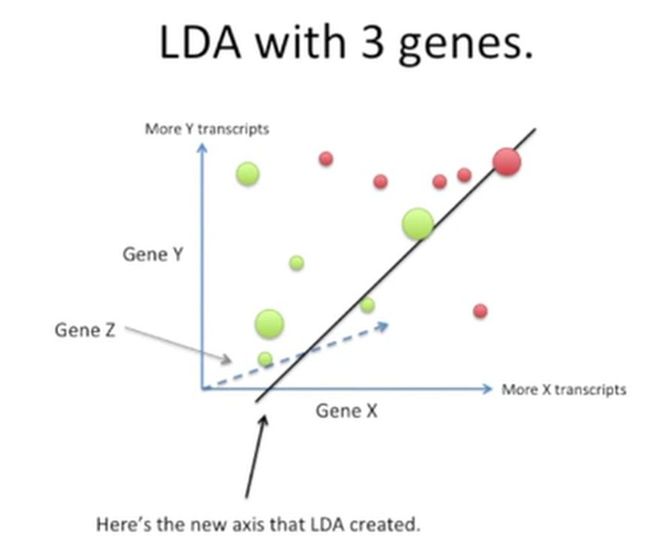
我们看一下LDA处理3个基因的情况,如下所示:
上图中的新坐标轴就是通过LDA方法创建的,此时,将所有的数据都投射到这个坐标轴上,它们的区分度就很好了,即保证了两类数据均值的间距最大,又最大程度地降低了数据的变异程度,如下所示:
复杂情况
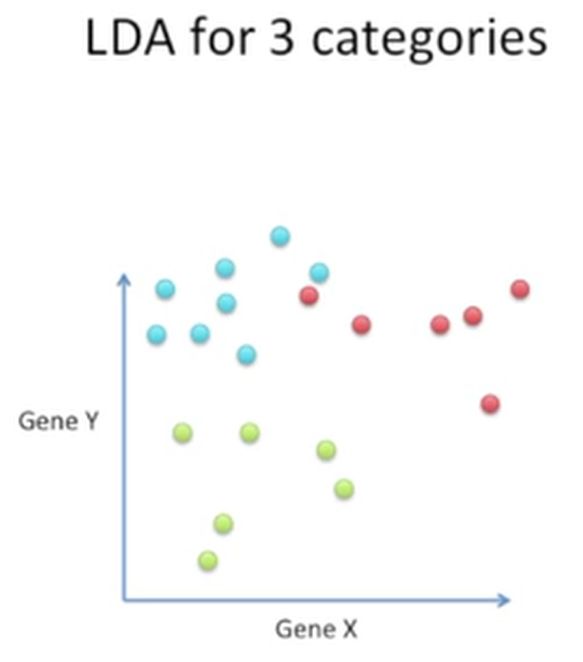
如果我们有3个分类,就像下面的这个样子,我们有3个分类,只有2个基因,如何做?
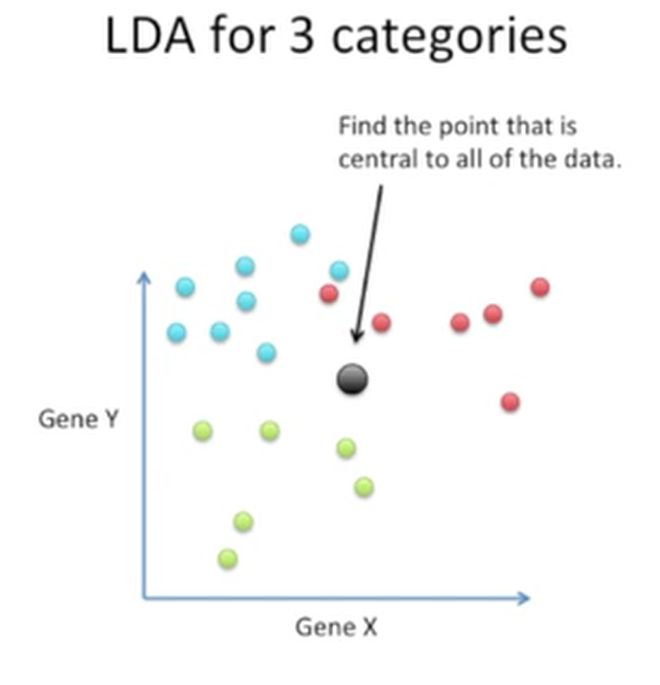
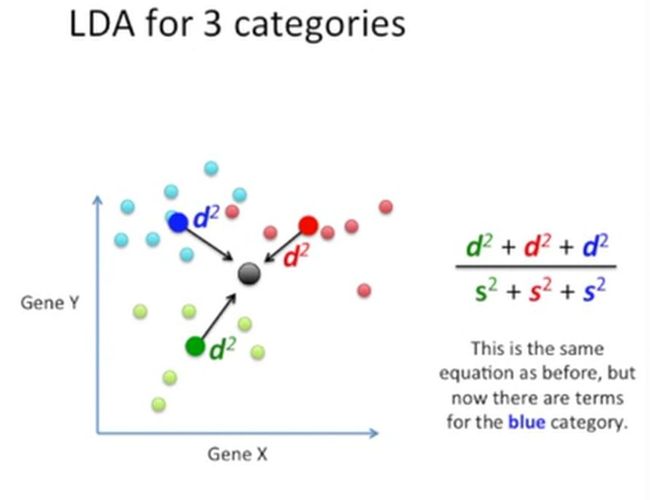
首选,我们要计算第一差分(first difference),它是一个点,这个点是所有点的中心,如下所示:
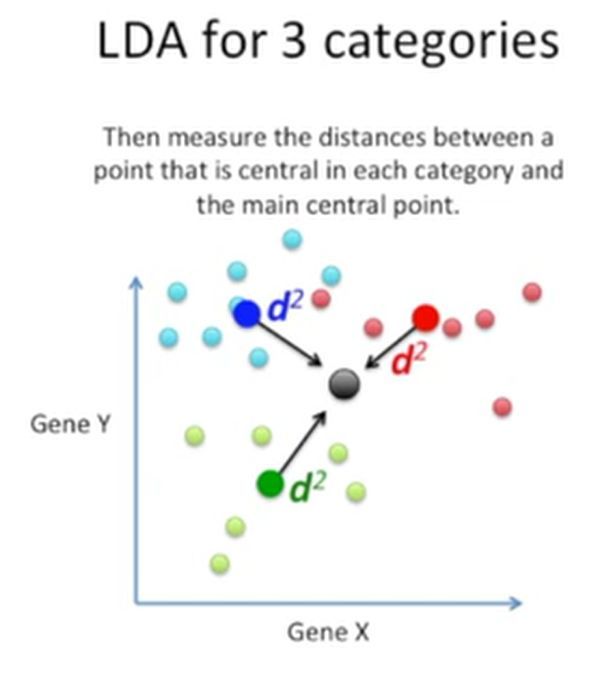
然后计算这个点与3个分类的中心的点(不太理解这个中心点是均值,还是中位数)的距离,如下所示:
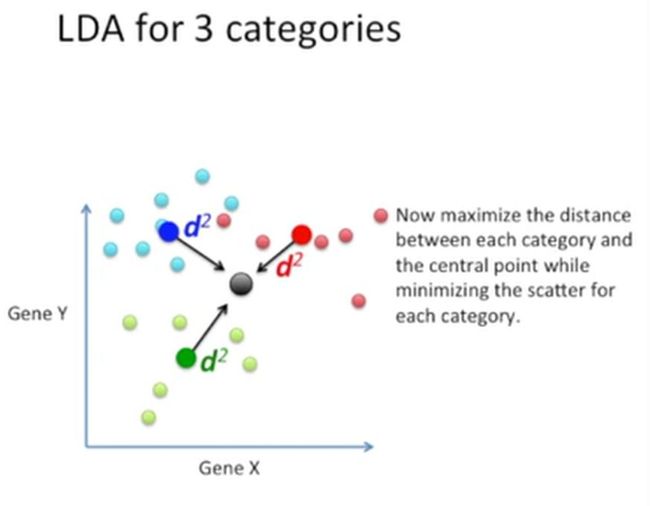
此时,再保证这三个距离最大,同时保证这三个分类投射到新的坐标轴上的点的离散程度最小,如下所示:
换成公式就是下面的样子:
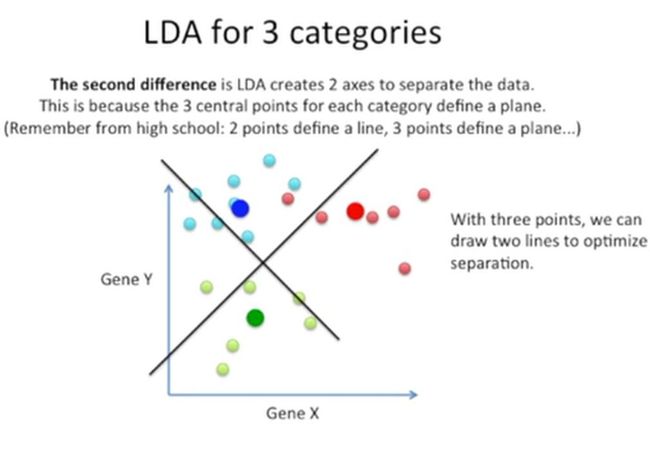
这个公式与前面的基本上一样,唯一的区别就是多了一个新的分类。接着,我们要找第二差分(second difference),这是LDA要创建的用于区分数据的2个坐标轴,这是因为三个分类的3个中心点能够定义一个平面,此时,我们绘制出两条线(也就是新的坐标系)来优化对这三个分类的分类,如下所示:
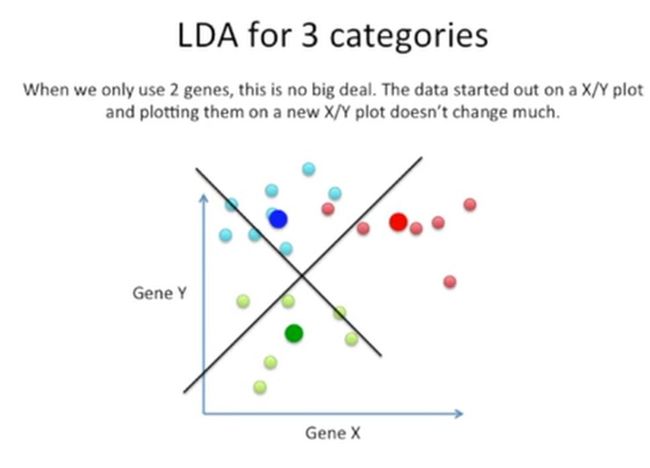
由于我们只使用了2个基因,因此绘制这个新坐标系很容易,如下所示:
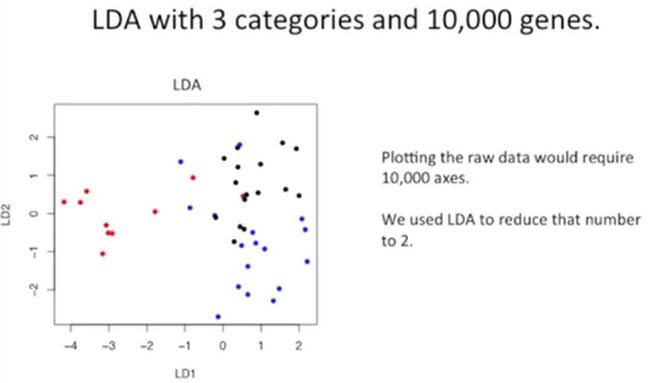
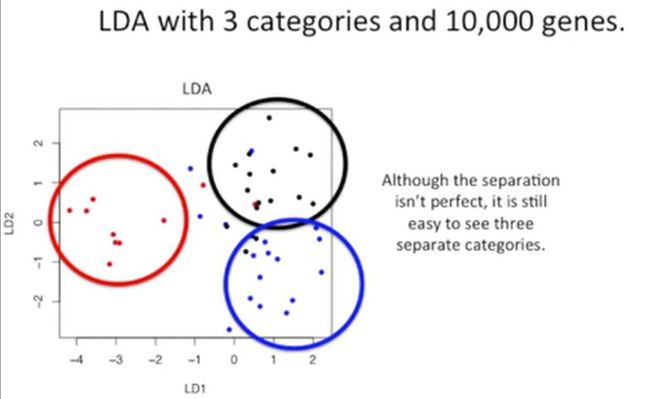
但是,如果我们有10000个基因的话,就意味着我们需要把这10000维降为两组,由于我们前面提到过,用2维坐标就能区分出3个分类,那么,我们如果有10000个基因,也能把它们降为2维的话,就很不错了,如下所示:
下图是用LDA实现的降维结果,如下所示:
虽然这种降维还不是太完美,很容易发现有一些分类还存在重叠,如下所示:
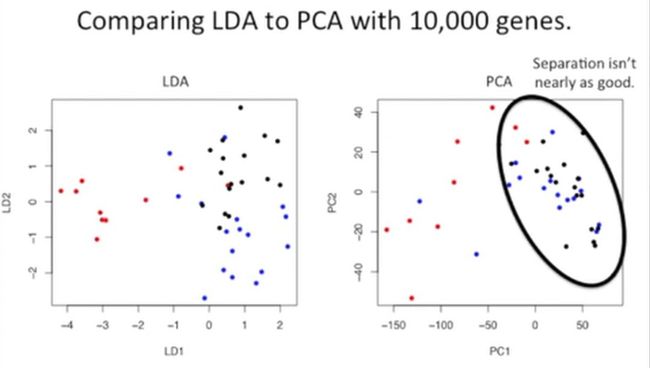
但是,我们比较一下LDA和PCA的降维效果,显然LDA已经做得更好一些了,如下所示:
此时,我们再来看一下PCA与LDA的相似性。
第一,在新的坐标轴上,它们都是按重要性进行排序的。其中PC1(PCA创建的第1个新坐标轴)能解释数据的最大变异,PC2(第2个新坐标轴)能解释数据次大的变异。而在LDA中,LD1(LDA创建的第1个坐标轴)能解释分类之间的最大变异,而LD2其次解释次大的变异。
第二,这两种方法都能够让你更观察哪些基因参与了分类,并形成了新的坐标,如下所示:
总结
LDA类似PCA,它们都是降维方法。PCA研究的是某个变量(这里指的是基因)的最大变异。LDA则是用这些变量(这里指的是基因)能够更大程度地区分已知分类。