不再惧怕!二叉树结构相关算法总结
写在前面
树结构对于程序员来说应该不陌生,特别是二叉树,基本只要接触算法这一类的都一定会碰到的,所以我打算通过一篇文章,对二叉树结构的相关算法进行总结汇总,思路和代码实现相结合,让你不在惧怕二叉树。(ps:后面我还想写一篇树结构的高级篇,就是多叉数,就是对我平时看算法论文碰到的一些新奇的算法,比如B树、B+树,还有我一种叫做Bed树的新奇算法等等)
单纯就是想分享技术博文,还想说一句就是,如果觉得有用,请点个关注、给个赞吧,也算对我来说是个宽慰,毕竟也得掉不少头发,嘿嘿嘿
递归
迭代
DFS
BFS
莫里斯遍历
AVL
预备
下面的思路讲解中,我会给出一个类伪代码的思路,然后进行相关说明,也就是一种思路框架,有了思路框架,以后碰到问题就直接交给框架完成。本文主要说一下二叉搜索树(Binary Search Tree,简称 BST),BST是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。如下就是一个符合定义的 BST:

后面如果遇到特殊的思路结构,如多叉树,我会特别说明。首先我们先给出二叉树的节点定义(这个定义应该不陌生吧,有刷算法题都会碰到)。
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
递归
不过这里要说明一点的是,在伪代码中的“进行想要的操作”的位置,不一定就在我放置的位置,具体位置还需要我们根据不同的实际需求进行判断。不过因为前中后序的遍历,递归进入的时机应该需要和我的一样。
先序遍历
遍历根节点,如果根节点为空,返回;否则,遍历根节点,然后先序遍历左子树,再先序遍历右子树。
public void preorderTraverse(TreeNode root){
System.out.print(node.val+" ");
preorderTraverse(root.left);
preorderTraverse(root.right);
}
中序遍历
路过根节点,如果根节点为空,返回;否则,中序遍历左子树,然后遍历根节点,再中序遍历右子树。
public void inorderTraverse(TreeNode root){
inorderTraverse(root.left);
System.out.print(node.val+" ");
inorderTraverse(root.right);
}
后序遍历
路过根节点,如果根节点为空,返回;否则,后序遍历左子树,再后序遍历右子树,最后遍历根节点。
public void postorderTraverse(TreeNode root){
postorderTraverse(root.left);
postorderTraverse(root.right);
System.out.print(node.val+" ");
}
迭代(非递归)
我们使用迭代的思想,其实就是利用循环和栈来模拟递归的操作,上面递归的操作,其实就是一个不断将自己以及左右子节点进行压栈和出栈的过程,如果理解了上面的算法下面的算法就好理解了
前序遍历
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root==null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode res = stack.pop();
if(res.right != null)
stack.push(res.right);
if(res.left != null)
stack.push(res.left);
list.add(res.val);
}
return list;
}
中序遍历
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root==null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while(curr != null || !(stack.isEmpty())){
if(curr!= null){
stack.push(curr);
curr = curr.left;
}else{
curr = stack.pop();
list.add(curr.val);
curr = curr.right;
}
}
return list;
}
后序遍历
我们可以很简单的实现另一种遍历:”根->右->左“遍历。虽然这种遍历没有名字,但是他是后序遍历的反序。所以我们可以利用两个栈,利用栈的LIFO特点,来实现后续遍历。
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root==null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode res = stack.pop();
if(res.left != null)
stack.push(res.left);
if(res.right != null)
stack.push(res.right);
list.add(res.val);
}
list.reserve();
return list;
}
深度优先搜索(DFS)
其实,二叉树的先序遍历,中序遍历,后序遍历,都是深度优先搜索,深搜是一种思想,并不具体指代实现方式,你可以使用递归,也可以使用栈来实现,所以上面提到的都是深度优先搜索的实现方式,毕竟“深度优先”嘛。
那在这里我就是提几个实际的应用的例子,加深一下印象。
*二叉树的最大深度
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left,right)+1;
}
*二叉树的镜像
public void Mirror(TreeNode root) {
if(root!=null){
if(root.left!=null || root.right!= null){
TreeNode temp =root.left;
root.left=root.right;
root.right=temp;
}
Mirror(root.left);
Mirror(root.right);
}
}
*对称二叉树
boolean isSymmetrical(TreeNode pRoot){
if(pRoot == null)
return true;
return real(pRoot.left,pRoot.right);
}
public boolean real(TreeNode root1,TreeNode root2){
if(root1 == null && root2 == null){
return true;
}
if(root1 ==null || root2 == null){
return false;
}
if(root1.val != root2.val){
return false;
}
return real(root1.left,root2.right)&&real(root1.right,root2.left);
}
*路径总和
public class Solution {
private ArrayList<Integer> list = new ArrayList<Integer>();
private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
if(root == null)
return listAll;
list.add(root.val);
target -= root.val;
if(target == 0 && root.left==null && root.right == null){
listAll.add(new ArrayList<Integer>(list));
}
FindPath(root.left,target);
FindPath(root.right,target);
list.remove(list.size()-1);
return listAll;
}
}
*重建二叉树
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
return reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
}
public TreeNode reConstructBinaryTree(int [] pre,int startpre,int endpre,int [] in,int startin,int endin){
if(startpre > endpre || startin > endin){
return null;
}
TreeNode root = new TreeNode(pre[startpre]);
for(int i =startin;i<=endin;i++){
if(in[i] == pre[startpre]){
root.left = reConstructBinaryTree(pre,startpre+1,startpre+i-startin,in,startin,i-1);
root.right = reConstructBinaryTree(pre,startpre+i-startin+1,endpre,in,i+1,endin);
}
}
return root;
}
*二叉搜索树的最近公共祖先
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q){
return root;
}
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left!=null && right!=null){
return root;
}
return left!=null?left:right;
}
}
*二叉树的序列化和反序列化
序列化:
public String serialize(TreeNode root) {
if (root == null) {
return null;
}
// 利用二叉树的层次遍历方式进行序列化
StringBuilder res = new StringBuilder();
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.remove();
if (node != null) {
res.append(node.val).append(",");
queue.add(node.left);
queue.add(node.right);
} else {
res.append("null,");
}
}
return res.toString();
}
反序列化:
public TreeNode deserialize(String data) {
if (data == null || data.length() == 0) {
return null;
}
String[] dataArr = data.split(",");
// 层次遍历逆向还原二叉树
int index = 0;
TreeNode root = toNode(dataArr[index]);
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (index < dataArr.length - 2 && !queue.isEmpty()) {
TreeNode cur = queue.remove();
// 添加左子节点
TreeNode leftNode = toNode(dataArr[++index]);
cur.left = leftNode;
// 队列中的节点用于为其赋值孩子节点,若该节点本身为 null,
// 没有孩子节点,便不再添加到队列中,下同理
if (leftNode != null) {
queue.add(leftNode);
}
// 添加右子节点
TreeNode rightNode = toNode(dataArr[++index]);
cur.right = rightNode;
if (rightNode != null) {
queue.add(rightNode);
}
}
return root;
}
private TreeNode toNode(String val) {
if (!"null".equals(val)) {
return new TreeNode(Integer.parseInt(val));
} else {
return null;
}
}
广度优先搜索(BFS)
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。
- 如果找到目标,则结束搜索并回传结果。
- 否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。
- 重复步骤2。
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
List<TreeNode> quene = new ArrayList<TreeNode>();
if(root == null){
return res;
}
quene.add(root);
while(quene.size()!=0){
int count = quene.size();
List<Integer> list = new ArrayList<Integer>();
while(count>0){
TreeNode temp =quene.remove(0);
list.add(temp.val);
if(temp.left!=null){
quene.add(temp.left);
}
if(temp.right!=null){
quene.add(temp.right);
}
count--;
}
res.add(list);
}
return res;
}
莫里斯遍历(Morris)
通常我们对于二叉树进行遍历时,使用递归遍历或是基于栈来遍历,这两种方法都拥有最差为O(n)的空间复杂度(递归方法会在递归调用上浪费更多的时间),以及O(n)的时间复杂度。对于时间复杂度来说,由于需要遍历每个元素一次,所以O(n)已是最优情况。如此只能对空间进行优化。Morris遍历如何做到的呢?首先我们需要分析递归和基于栈的遍历它们为什么有O(n)的空间占用。以下图这个简单的二叉树遍历为例:
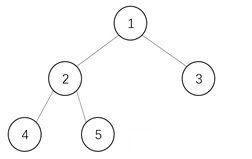
例如进行中序遍历(LDR),从1开始:
- 1有左孩子2,将1放入栈中,移动到节点2;
- 2有左孩子4,将2放入栈中,移动到节点4;
- 4左孩子为空,输出节点4,此时节点4右孩子也为空,弹栈回到节点2;
- 输出节点2,节点2有右孩子5,移动到节点5;
- 5左孩子为空,输出节点5,此时节点5右孩子也为空,弹栈回到节点1;
- …
从上面分析可以得知,传统遍历利用空间存储未实现全部操作的父节点,比如对于1节点,一开始进行L操作,没有进行D、R操作所以需要存储起来。为解决这一问题,Morris算法用到了”线索二叉树”的概念,利用叶节点的左右空指针指向某种遍历顺序的前驱节点或后继节点。Morris算法中序遍历流程:
- 设置节点1为Current节点;
- Current节点不为空,且有左孩子,于是找到节点1左子树中的最右侧节点,即节点5,使其右孩子指针指向自己,即link1;
- Current节点移动到左孩子节点2,并删除父节点的左指针,使其指向为null,即删除erase1;
- 节点2不为空,且有左孩子,于是找到节点2左子树中最右侧节点,即节点4,使其右孩子指针指向自己,即link2;
- Current节点移动到左孩子节点4,并删除父节点的左指针,使其指向为null,即删除erase2;
- 节点4左孩子为空,输出节点4,移动到右孩子节点2;
- 节点2无左孩子(指针指向null),输出节点2,移动到右孩子节点5;
- 节点5无左孩子,输出节点5,移动到右孩子节点1;
- 节点2无左孩子(指针指向null),输出节点1,移动到右孩子节点3;
- …
void Morris_inorderTraversal(TreeNode root) {
TreeNode curr = root;
TreeNode pre;
while (curr != null) {
if (curr.left == null) { // 左孩子为空
System.out.print(curr.val+" ");
curr = curr.right;
}
else { // 左孩子不为空
// 找左子树中的最右节点
pre = curr.left;
while (pre.right != null) {
pre = pre.right;
}
// 删除左孩子,防止循环
pre.right = curr;
TreeNode temp = curr;
curr = curr.left;
temp.left = null;
}
}
}
AVL树
AVL 树是一种平衡二叉树,平衡二叉树递归定义如下:
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
为了保证二叉树的平衡, AVL 树引入了所谓监督机制,就是在树的某一部分的不平衡度超过一个阈值后触发相应的平衡操作。保证树的平衡度在可以接受的范围内。既然引入了监督机制,我们必然需要一个监督指标,以此来判断是否需要进行平衡操作。这个监督指标被称为“平衡因子(Balance Factor)”。定义如下:
- 平衡因子: 某个结点的左子树的高度减去右子树的高度得到的差值。
基于平衡因子,我们就可以这样定义 AVL 树。
- AVL 树: 所有结点的平衡因子的绝对值都不超过 1 的二叉树。
为了计算平衡因子,我们自然需要在节点中引入高度这一属性。在这里,我们把节点的高度定义为其左右子树的高度的最大值。因此,引入了高度属性的 AVL 树的节点定义如下:
public class TreeNode {
int val;
int height;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
这里的节点和上面的不同的地方在于,我们多加了一个高度,用来记录每个节点的高度,如何得到每个节点的高度很简单,前面讲的算法中任何一种思路都可以实现,我这里就不赘述了,不过这里要多说一点的是,与之对应地,我们在进行如下操作时需要更新受影响的所有节点的高度:
- 在插入结点时, 沿插入的路径更新结点的高度值
- 在删除结点时(delete),沿删除的路径更新结点的高度值
我们重新定义了节点之后,有了高度属性,计算平衡因子的操作就得以很简单的实现,也就是某个节点的平衡因子=左节点高度-右节点高度。
当平衡因子的绝对值大于 1 时,就会触发树的修正,或者说是再平衡操作。
树的平衡化操作
二叉树的平衡化有两大基础操作: 左旋和右旋。左旋,即是逆时针旋转;右旋,即是顺时针旋转。这种旋转在整个平衡化过程中可能进行一次或多次,这两种操作都是从失去平衡的最小子树根结点开始的(即离插入结点最近且平衡因子超过1的祖结点)。其中,右旋操作示意图如下
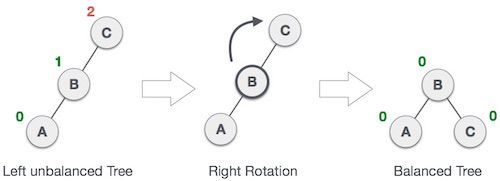
所谓右旋操作,就是把上图中的 B 节点和 C 节点进行所谓“父子交换”。在仅有这三个节点时候,是十分简单的。但是当 B 节点处存在右孩子时,事情就变得有点复杂了。我们通常的操作是:抛弃右孩子,将之和旋转后的节点 C 相连,成为节点 C 的左孩子。这样,对应的代码如下。
TreeNode treeRotateRight(TreeNode root) {
TreeNode left = root.left;
root.left = left.right; // 将将要被抛弃的节点连接为旋转后的 root 的左孩子
left.right = root; // 调换父子关系
left.height = Math.max(treeHeight(left.left), treeHeight(left.right))+1;
right.height = Math.max(treeHeight(right.left), treeHeight(right.right))+1;
return left;
}
而左旋操作示意图如下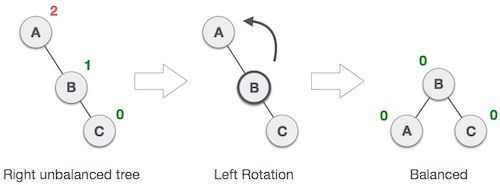
左旋操作和右旋操作十分类似,唯一不同的就是需要将左右互换下。我们可以认为这两种操作是对称的。代码如下:
TreeNode treeRotateLeft(TreeNode root) {
TreeNode right = root.ight;
root.right = right.left;
right.left = root;
left.height = Math.max(treeHeight(left.left), treeHeight(left.right))+1;
right->height = Math.max(treeHeight(right.left), treeHeight(right.right))+1;
return right;
}
需要平衡的四种情况
- LL 型
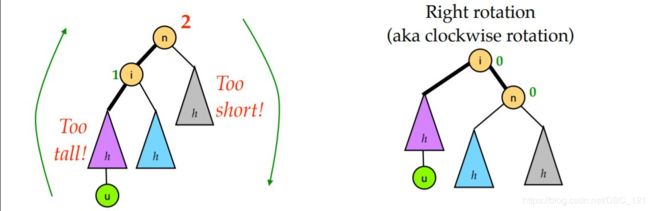
所谓 LL 型就是上图左边那种情况,即因为在根节点的左孩子的左子树添加了新节点,导致根节点的平衡因子变为 +2,二叉树失去平衡。对于这种情况,对节点 n 右旋一次即可。
- RR 型
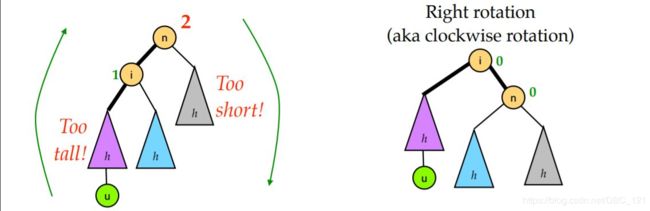
RR 型的情况和 LL 型完全对称。只需要对节点 n 进行一次左旋即可修正。
- LR 型
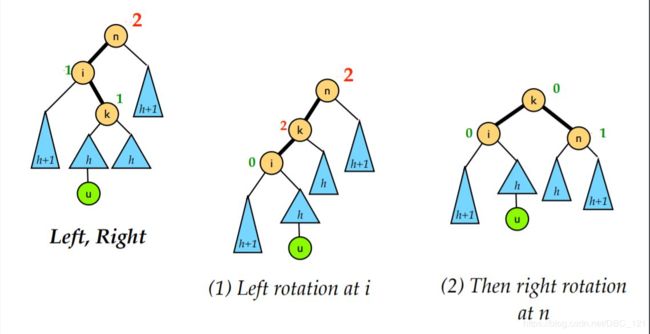
LR 就是将新的节点插入到了 n 的左孩子的右子树上导致的不平衡的情况。这时我们需要的是先对 i 进行一次左旋再对 n 进行一次右旋。
- RL 型
RL 就是将新的节点插入到了 n 的右孩子的左子树上导致的不平衡的情况。这时我们需要的是先对 i 进行一次右旋再对 n 进行一次左旋。
这四种情况的判断很简单。我们根据破坏树的平衡性(平衡因子的绝对值大于 1)的节点以及其子节点的平衡因子来判断平衡化类型。
平衡化操作的实现如下:
int treeGetBalanceFactor(TreeNode root) {
if(root == NULL)
return 0;
else
return x.left.height - x.right.height;
}
TreeNode treeRebalance(TreeNode root) {
int factor = treeGetBalanceFactor(root);
if(factor > 1 && treeGetBalanceFactor(root.left) > 0) // LL
return treeRotateRight(root);
else if(factor > 1 && treeGetBalanceFactor(root.left) <= 0) { //LR
root.left = treeRotateLeft(root.left);
return treeRotateRight(temp);
} else if(factor < -1 && treeGetBalanceFactor(root.right) <= 0) // RR
return treeRotateLeft(root);
else if((factor < -1 && treeGetBalanceFactor(root.right) > 0) { // RL
root.right = treeRotateRight(root.right);
return treeRotateLeft(root);
} else { // Nothing happened.
return root;
}
}
这里推荐一个AVL树动态化的网站,可以通过动态可视化的方式理解AVL
