图像压缩算法

图像压缩算法

---

声明：引用请注明出处http://blog.csdn.net/lg1259156776/

---

理论基础

香农的信息论，在不产生任何失真的前提下，通过合理的编码，对于每个信源符号分配不等长的码字，平均码长可以任意接近于信源的熵。在这个理论框架下产生了几种不同的无失真的信源编码方法：哈夫曼编码，算术编码、字典编码等。后来出现了更多的编码方式：如KLT编码、分形编码、模型编码、子带编码和基于小波的编码方法。

---

压缩的必要性和可能性

1. 存储和传输上的消耗。
2. 图像数据的冗余数据：同一帧临近位置的数据相同或相似；连续帧图像数据有大量相同的数据；人眼对图像分辨率的局限性、监视器显示分辨率的限制，容许一定限度的失真。

---

方法简介

基于信息论角度

1. 冗余度压缩方法：（无损压缩），在数学上可逆：哈夫曼编码-算术编码-行程编码-Lempel-zev 编码
2. 信息量压缩方法：（有损压缩），解码图像与原始图像有差：预测编码-频率域方法（正交变换编码如DCT、子带编码）-空间域方法（统计分块编码）-模型方法（分形编码、模型编码）-基于重要性（粒子、子采样、比特分配、矢量量化）

按照压缩技术所依据和使用的数学方法进行分类

1. 预测编码：基本思想是根据数据统计特性得到预测值，然后传输图像像素与其预测值的差值信号，使传输的码率降低，达到压缩的目的。
2. 统计编码：主要针对无记忆信源，根据信息码字出现概率的分布特征而进行压缩编码，寻找概率与码字长度间的最优匹配，其编码的实质就是用短码来表示较大的码字，而用长码表示出现概率较小的码字。常用的有：行程编码、哈夫曼编码和算术编码三种。
3. 变换编码：基本思想是利用图像块内像素之间的相关性，把图像变换到一组新的基(一般是频率域)上，使得能量集中到少数几个变换系数上，通过存储这些系数达到压缩数据的目的。常用的有：DCT-整数DCT-小波变换。

---

图像压缩编码的评价标准

1. 一个是对图像质量的评价：客观和主观。主观就是用人去观察评分；客观就是对压缩还原后的图像与原始图像误差进行定量计算。一般都是进行某种平均，得到均方误差；另一种是信噪比。
2. 一个是对图像压缩效果的评价：压缩比=原始图像每像素的比特数同压缩后图像每像素的比特数的比值。

---

统计编码之哈夫曼编码

1. 基本原理：将使用次数多的代码转换为长度较短的代码，而是用次数少的可以使用较长的编码，并保持编码的唯一可解性。
2. 基本原则：保证权值和最小（字符统计数字x字符编码长度之和）
3. 基本步骤：(1) 从左到右将信源符号频率从小到大的顺序排列 (2)将将两个最小概率进行组合相加，并继续这个步骤，始终将较高的概率分支放到上部，直到概率达到1为止 (3)对每对组合中上边的一个都指定为1，下边的一个指定为0，或者相反。(4)画出由每个信源符号到达概率为1.0处的路径，记下沿路径遇到的各个1和0。(5)对每个信源符号都写出1和0序列，则最后便得到了哈夫曼编码。

这是一个哈夫曼树，常用于最佳判定，是最优二叉树，是一种带权路径长度最短的二叉树。树中所有叶节点的权值乘以其到根节点的长度记为

---

统计编码之算术编码

在图像数据压缩标准如JPEG中扮演重要角色。与哈夫曼的变长编码不同，算术编码生成的是非码块，生成的是一个区间。

基本原理

算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔，消息越长，编码表示它的间隔就越小，表示这一间隔所需的二进制位就越多。 算术编码用到两个基本的参数：符号的概率和它的编码间隔。

算术编码是一种无失真的编码方法，能有效地压缩信源冗余度，属于熵编码的一种。算术编码的一个重要特点就是可以按分数比特逼近信源熵，突破了Haffman编码每个符号只不过能按整数个比特逼近信源熵的限制。对信源进行算术编码，往往需要两个过程，第一个过程是建立信源概率表，第二个过程是对信源发出的符号序列进行扫描编码。而自适应算术编码在对符号序列进行扫描的过程中，可一次完成上述两个过程，即根据恰当的概率估计模型和当前符号序列中各符号出现的频率，自适应地调整各符号的概率估计值，同时完成编码。尽管从编码效率上看不如已知概率表的情况，但正是由于自适应算术编码具有实时性好、灵活性高、适应性强等特点，在图像压缩、视频图像编码等领域都得到了广泛的应用。
那为什么还要采用自适应模型呢？因为静态模型无法适应信息的多样性，例如，以上得出的概率分布没法在所有待压缩信息上使用，为了能正确解压缩，必须再消耗一定的空间保存静态模型统计出的概率分布，保存模型所用的空间将使我们重新远离熵值。其次，静态模型需要在压缩前对信息内字符的分布进行统计，这一统计过程将消耗大量的时间，使得本来就比较慢的算术编码压缩更加缓慢。另外还有最重要的一点，对较长的信息，静态模型统计出的符号概率是该符号在整个信息中的出现概率，而自适应模型可以统计出某个符号在某一局部的出现概率或某个符号相对于某一上下文的出现概率，换句话说，自适应模型得到的概率分布将有利于对信息压缩（可以说结合上下文的自适应模型的信息熵建立在更高的概率层次上，其总熵值更小），好的基于上下文的自适应模型得到的压缩结果将远远超过静态模型。
　　通常用“阶”（order）这一术语区分不同的自适应模型。刚刚上面的例子采用的是0阶自适应模型，也就是说，该例子中统计的是符号在已输入信息中的出现概率，没有考虑任何上下文信息。如果我们将模型变成统计符号在某个特定符号后的出现概率，那么，模型就成为了 1 阶上下文自适应模型。举例来说，要对一篇英文文本进行编码，已经编码了 10000 个英文字符，刚刚编码的字符是 t，下一个要编码的字符是 h。如果在前面的编码过程中已经统计出前 10000 个字符中出现了 113 次字母 t，其中有 47 个 t 后面跟着字母 h。得出字符 h 在字符 t 后的出现频率是 47/113，我们使用这一频率对字符 h 进行编码，需要 -＝1.266位。
对比 0 阶自适应模型，如果前 10000 个字符中 h 的出现次数为 82 次，则字符 h 的概率是 82/10000，我们用此概率对 h 进行编码，需要 － = 6.930 位。考虑上下文因素的优势显而易见。我们还可以进一步扩大这一优势，例如要编码字符 h 的前两个字符是 gt，而在已经编码的文本中 gt 后面出现 h 的概率是 80%，那么只需要 0.322 位就可以编码输出字符h。此时，这种模型叫做 2 阶上下文自适应模型。
　　最理想的情况是采用 3 阶自适应模型。此时，如果结合算术编码，对信息的压缩效果将达到惊人的程度。采用更高阶的模型需要消耗的系统空间和时间至少在目前还无法让人接受，使用算术压缩的应用程序大多数采用 2 阶或 3 阶的自适应模型。
使用自适应模型的算术编码算法必须考虑如何为从未出现过的上下文编码。例如，在 1 阶上下文模型中，需要统计出现概率的上下文可能有 256 * 256 = 65536 种，因为 0 - 255 的所有字符都有可能出现在 0 - 255 个字符中任何一个之后。当我们面对一个从未出现过的上下文时（比如刚编码过字符 b，要编码字符 d，而在此之前，d 从未出现在 b 的后面），该怎样确定字符的概率呢？
　　比较简单的办法是在压缩开始之前，为所有可能的上下文分配计数为 1 的出现次数，如果在压缩中碰到从未出现的 bd 组合，我们认为 d 出现在 b 之后的次数为 1，并可由此得到概率进行正确的编码。使用这种方法的问题是，在压缩开始之前，在某上下文中的字符已经具有了一个比较小的频率。例如对 1 阶上下文模型，压缩前，任意字符的频率都被人为地设定为 1/65536，按照这个频率，压缩开始时每个字符要用 16 位编码，只有随着压缩的进行，出现较频繁的字符在频率分布图上占据了较大的空间后，压缩效果才会逐渐好起来。对于 2 阶或 3 阶上下文模型，情况就更糟糕，我们要为几乎从不出现的大多数上下文浪费大量的空间。
　　我们通过引入“转义码”来解决这一问题。“转义码”是混在压缩数据流中的特殊的记号，用于通知解压缩程序下一个上下文在此之前从未出现过，需要使用低阶的上下文进行编码。举例来讲，在 3 阶上下文模型中，我们刚编码过 ght，下一个要编码的字符是 a，而在此之前，ght 后面从未出现过字符 a，这时，压缩程序输出转义码，然后检查 2 阶的上下文表，看在此之前 ht 后面出现 a 的次数；如果 ht 后面曾经出现过 a，那么就使用 2 阶上下文表中的概率为 a 编码，否则再输出转义码，检查 1 阶上下文表；如果仍未能查到，则输出转义码，转入最低的 0 阶上下文表，看以前是否出现过字符 a；如果以前根本没有出现过 a，那么我们转到一个特殊的“转义”上下文表，该表内包含 0 - 255 所有符号，每个符号的计数都为 1，并且永远不会被更新，任何在高阶上下文中没有出现的符号都可以退到这里按照 1/256 的频率进行编码。“转义码”的引入使我们摆脱了从未出现过的上下文的困扰，可以使模型根据输入数据的变化快速调整到最佳位置，并迅速减少对高概率符号编码所需要的位数。

可以参考
http://blog.csdn.net/china_video_expert/article/details/5927719

---

统计编码之行程编码

将一行中颜色值相同的相邻象素用一个计数值和该颜色值来代替。例如aaabccccccddeee可以表示为3a1b6c2d3e。如果一幅图象是由很多块颜色相同的大面积区域组成，那么采用行程编码的压缩效率是惊人的。然而，该算法也导致了一个致命弱点，如果图象中每两个相邻点的颜色都不同，用这种算法不但不能压缩，反而数据量增加一倍。

行程编码的可行性讨论：
行程编码的压缩方法对于自然图片来说是不太可行的，因为自然图片像素点错综复杂，同色像素连续性差，如果硬要用行程编码方法来编码就适得其反，图像体积不但没减少，反而加倍。鉴于计算机桌面图，图像的色块大，同色像素点连续较多，所以行程编码对于计算机桌面图像来说是一种较好的编码方法。行程编码算法特点：有算法简单、无损压缩、运行速度快、消耗资源少等优点。
具体的算法Matlab实验，参看文件夹：Digital Image Processing\Algorithm of Digital Image Processing\3-Compresser\1-matlab book example：ex0503.m

大致方法是：遍历所有像素点，一行一行的。从第一个开始，如果下一个相同，则num++，直到下一个不同值开始，等等。

可以参看http://blog.csdn.net/zuzubo/article/details/1598009

---

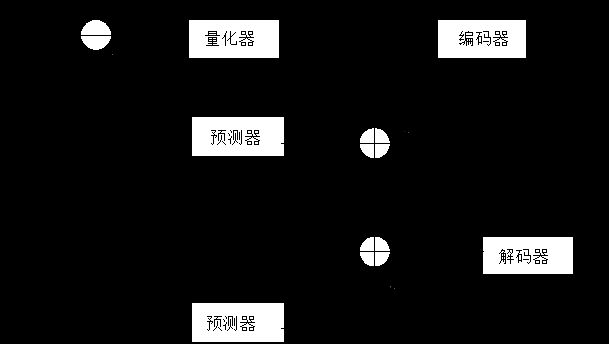
预测编码之差分脉冲编码调制编码（DPCM）

可以参看 http://bbs.csdn.net/topics/210083337
DPCM是differential pulse code modulation的缩写，也就是差分脉冲编码调制的意思。他的主要思想是通过已知的数据预测下一个数据，然后传递预测值与实际值之间的差值。

如果直接使用DPCM进行编码的话，是得不到什么压缩的效率的。缘故是，需要传输或保存的是预测值后的值与实际值之间的差值，这与原来的数据占用同样的空间。

为了满足我们原始的压缩数据的动机，你可以对这些差值进行各种各样的编码。因为，大部分情况下，差值都是像1,1,1,2,3,5,5,5之类的数。可以对它们进行通常的游程编码或者huffman编码，运气好的话能够得到很大的压缩比。

这样做会有一个很大的弊端。因为有些数据可能之间的联系会呈线性或者某种连续函数的性质。但是大部分情况下，数据的分布还是有一定的离散性的。当数据之间出现很大的跳跃的时候，这种方法就显得很苍白无力了。

我们可以这么做，每次对得到的差值用一个随着差值大小变化的数来除。这样就可以随着差值的变化，不断调整比例因子。这样出现较大的跳跃时也能把我们要存储的差值限定在一个较小的范围之内。
如果你现在有些迷惑，没事，我们换种方式来说明一下。
假设差值是 diff，也就是 diff = X~i - Xi，那么，diff就有可能变动很大，如果引入一个不断变化的因子iDelta,那么，diff’ = diff / iDelta，而对于iDelta，每当diff变大的时候，他就变大比较大，当diff变得比较小的时候，他就相应的减小。这样，我们的diff’就能保持相对的稳定了。通过iDelta的引入，可以使得我们的DPCM编码自动的适应数据间大幅度的跳跃。这就是自适应脉冲编码调制，ADPCM的主要思想。

你现在可能会想，iDelta到底怎么变化，才能自动的匹配diff的变化?一种可行的方法就是，把它定义为diff的一个函数，这个函数根据不同的diff的值的大小取不同大小的值。通常我们会做一个iDelta值的表，通过diff作为索引，这样，就可以根据不同的diff值，iDelta就可以作相应的变化了。

---

预测编码之运动补偿

主要用于视频图像编码中
是一种描述相邻帧差别的方法，具体来讲是指描述前面一帧的每个小块怎样移动到当前帧中的某个位置去。常用来被视频压缩/视频编码解码器用来减少视频序列中的空域冗余。
通常，图像帧是一组一组进行处理的。每组的第一帧在编码时不使用运动估计得方法，这种帧成为帧内编码帧，或I帧。该组中其他帧使用帧间编码帧，通常为P帧，这种编码方式成为IPPPP，表示编码的时候第一帧是I帧，其他帧是P帧。在进行预测的时候，不仅仅可以根据过去帧预测当前帧，还可以使用未来帧预测当前帧。即编码的顺序和播放的顺序是可以不同的。通常，这样的当前帧是使用过去和未来的I帧或者P帧同时进行预测的，成为双向预测帧即B帧。如：IBBPBBPBBPBB

---

预测编码之增量调制编码

模拟信号数字化方法：
一种把信号上的采样值作为预测值的单纯预测编码方式，是最简单的预测编码方式之一。将信号瞬时值与前一抽样时刻的量化值之差进行量化，而且只对差值的符号进行编码，不对大小编码。因此量化只限于正和负两个电平。接收端每收到一个“1”码，译码器的输出相对于前一个时刻上升一个量阶，当收到连“1”码时，表示信号持续增长。反之亦然。译码器的输出再经过低通滤波器滤除高频量化噪声，从而恢复原始信号。只要抽样频率足够高，量化阶矩大小适当，接收端的信号与原始信号就非常接近。

---

变换编码之主成分变换（KLT）

KLT的基本原理：假设一幅图像在某个通信信道中传输了M次，由于任何物理信道均存在随即干扰因素，接收到的图像系列总混杂有许多随机干扰信号，称之为随机图像集合，集合中各图象之间存在相关性但又不相等。KLT本质上市针对这类广泛的随机图像提出来，当对M个图像施加了KLT以后，变换后的M新图像组成的集合中各图象之间互不相关。由变换结果图像集中取有限个图像K（K<M）而恢复的图像僵尸原图像在统计意义上的最佳逼近。
参看 http://blog.csdn.net/tiandijun/article/details/20797817

---

变换编码之离散余弦变换（DCT）

JPEG图像格式的压缩算法采用的就是DCT。从原理上讲，可以对整幅图像进行DCT变换。但由于图像各个部分上细节的丰富程度不同，这种整体处理的方式效果不好。为此，发送者首先将输入图像分解为8x8或16x16的块，然后对每个图像块进行二维DCT变换，接着在对DCT系数进行量化，编码和传输，接受者通过对量化的DCT系数进行解码，并对图像块进行二维DCT反变换，最后拼接起来构成一幅完整的图像。对于一般的图像来讲，大多数的系数近似为0。所以，可以忽略之，并不影响效果。

---

变换编码之沃尔什-哈达玛变换

---

变换编码之小波变换

JPEG2000静态图像编码标准中的图像变换技术就采用了离散小波变换。最大的特点是在不丢失重要信息的同时，能以比较高的比率压缩图像，并且算法计算量小。

---

2015-9-23 艺少

转载于:https://www.cnblogs.com/huty/p/8519130.html