二叉树的前序、中序和后序遍历（递归和非递归的方法）
二叉树的前序、中序和后序遍历（递归和非递归的方法）
二叉树的基础概念
二叉树： 是每个节点最多只有两个分支的树结构。通常分支被称为”左子树“和”右子树“。二叉树的分支具有左右次序，不能随意颠倒。
下图是一棵二叉树
二叉树还有如下的性质：
- 二叉树的第 i i i 层至多有 2 i − 1 2^{i-1} 2i−1 个节点
- 深度为 k k k 的二叉树至多有 2 k − 1 2^k-1 2k−1 个节点
- 一颗含有 n n n 个节点的二叉树，它的深度至少为 l o g n + 1 logn+1 logn+1
- 对于任意一颗二叉树T，如果T的叶子节点数为 n 0 n_0 n0，度为2的节点个数为 n 2 n_2 n2，则 n 0 = n 2 + 1 n_0 = n_2+1 n0=n2+1
这里证明一下性质4：
对于一颗二叉树而言，他的每一个节点的度都做多为2，那么节点的总数 n n n ，就可以是 “度为零的节点 n 0 n_0 n0”+“度为一的节点 n_1” + “度为二的节点 N-2”，即
n = n 0 + n 1 + n 2 ( 1 ) n=n_0+n_1+n_2 \quad\quad\quad (1) n=n0+n1+n2(1)
那么度为0的节点没有孩子，度为1的节点有1个孩子，度为2的节点含有两个孩子，所以可以计算一颗二叉树孩子节点的总数为 0 × n 0 + 1 × n 1 + 2 × n 2 = n 1 + 2 n 2 0 \times n_0 + 1 \times n_1 + 2\times n_2 = n_1+2n_2 0×n0+1×n1+2×n2=n1+2n2，根节点不属于任何节点的孩子，所以总共的节点数
n = n 1 + 2 n 2 + 1 ( 2 ) n=n_1+2n_2+1 \quad\quad\quad (2) n=n1+2n2+1(2)
所以 ( 2 ) − ( 1 ) (2)-(1) (2)−(1) 可以得到 n 0 = n 2 + 1 n_0 = n_2+1 n0=n2+1
二叉树的遍历： 指的是从根节点出发，按照某种次序访问二叉树中所有节点，使得每个节点被访问一次且仅被访问一次。
这里介绍的是二叉树的先序、中序、后序遍历方法及其代码实现（包括递归和非递归方法）。
三种遍历方法的思想：
- 先序：根结点 —> 左子树 —> 右子树
- 中序：左子树—> 根结点 —> 右子树
- 后序：左子树 —> 右子树 —> 根结点
先序遍历
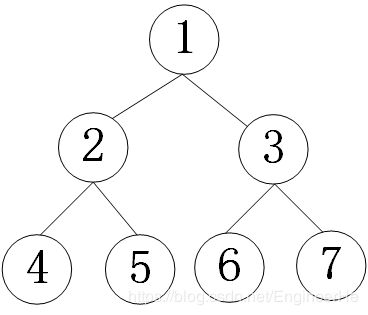
先序遍历，先访问根节点，然后先序遍历左子树，在先序遍历右子树（根左右），如下图所示，是二叉树的先序遍历步骤，输出结果为 [1,2,4,5,7,8,3,6]
采用递归的方法很简单，代码如下：
void recursionPreorder(TreeNode* root) {
if (root == NULL) {
return;
}
cout << root->val << " ";
recursionPreorder(root->left);
recursionPreorder(root->right);
}
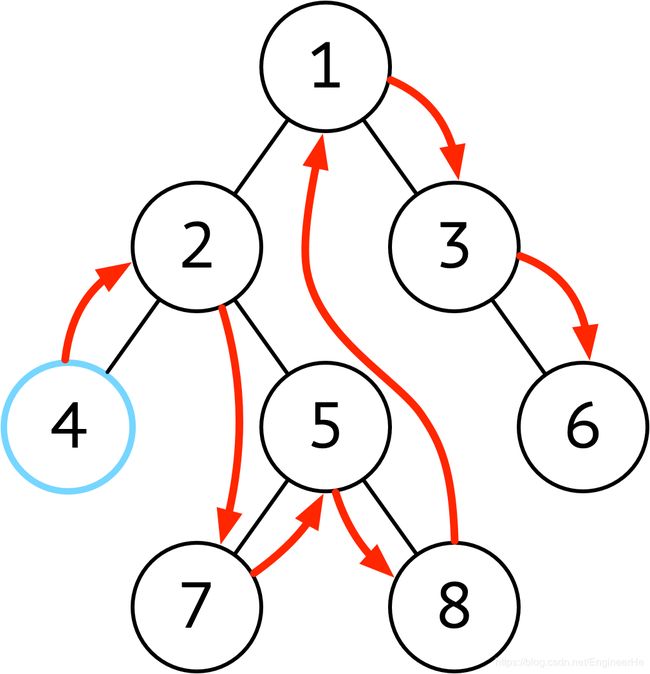
对于上述递归的方法，即如果符合条件就直接打印（或者存储），不符合的情况就递归，递归就是把数据压入栈中，那么使用非递归的方法就可以使用栈结构来存储左右节点，需要的时候再把节点弹出。对于先序遍历来讲，其顺序为 “根左右”，那么如果想从栈中弹出此顺序，就需要先压入右节点再压入左节点。这里我做了一个动画，描述一下使用栈是怎么实现先序遍历的
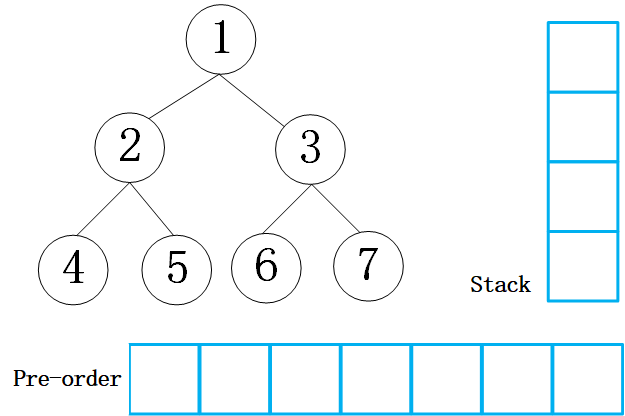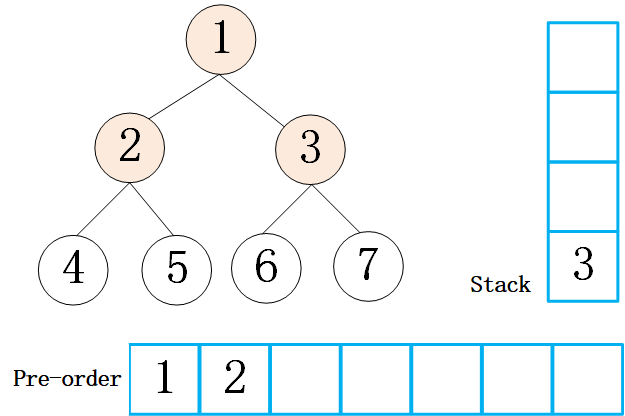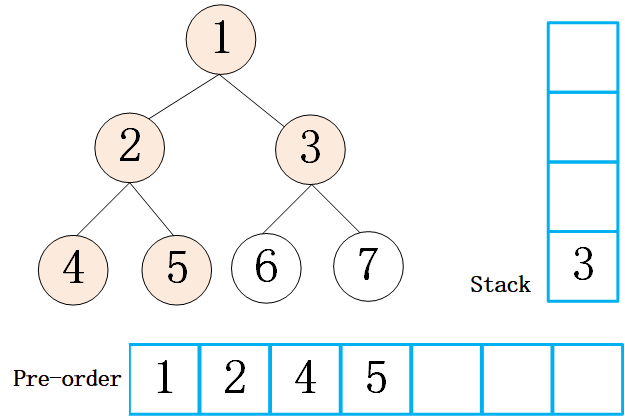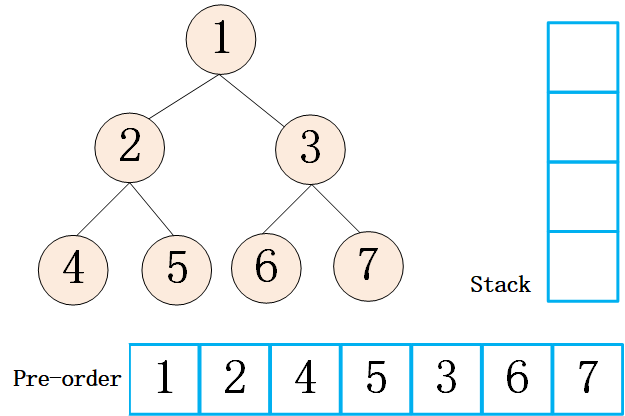
代码实现（非递归）
void preorder(TreeNode* root) {
if (root == NULL) {
return;
}
TreeNode* cur = root;
stack<TreeNode*> nodeStack;
nodeStack.push(cur);
while (!nodeStack.empty()) {
cur = nodeStack.top(); // 弹出栈顶
cout << cur->val << " ";
nodeStack.pop();
// 先压入右节点
if (cur->right) {
nodeStack.push(cur->right);
}
// 后压入左节点
if (cur->left) {
nodeStack.push(cur->left);
}
}
cout << endl;
}
中序遍历
中序遍历，中序遍历根节点的左子树，然后访问根节点，最后遍历右子树（左根右），如下图所示，是二叉树的中序遍历步骤，输出结果为 [4,2,7,5,8,1,3,6]。
递归的方法实现中序遍历，代码如下：
void recursionInorder(TreeNode* root) {
if (root == NULL) {
return;
}
recursionInorder(root->left);
cout << root->val << " ";
recursionInorder(root->right);
}
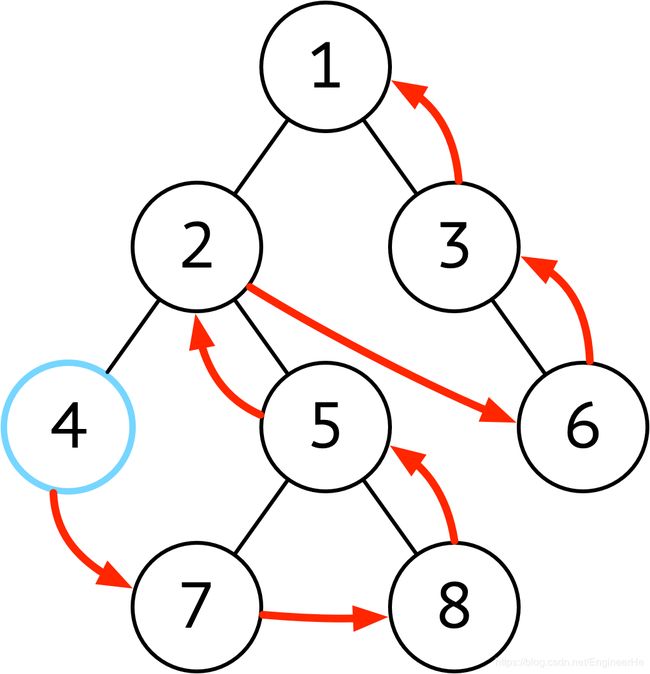
想实现非递归版本的，同样的使用栈的操作。在递归版本的代码中，先把左侧的所有的节点都压入栈中，然后弹出一个节点，同样的把弹出的节点的左孩子全部压入栈中，然后弹出，压入一个右节点。所以对于中序遍历来说，需要做的操作是，通过给定的节点，先把其所有的左孩子压入栈中；如果为空，同样的方式遍历右孩子。来一个动画继续说明一下这个过程：
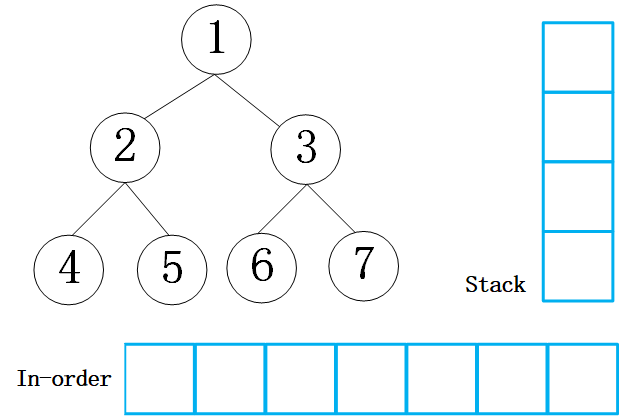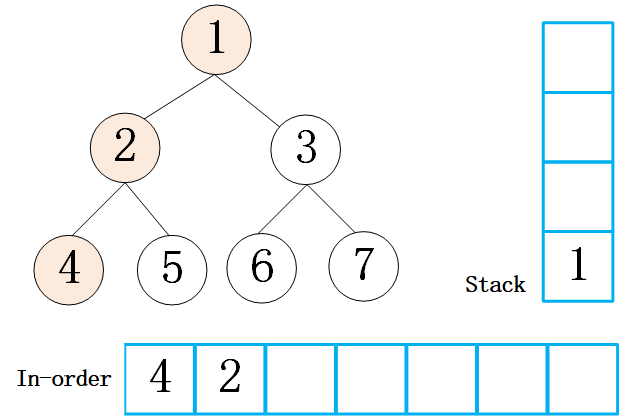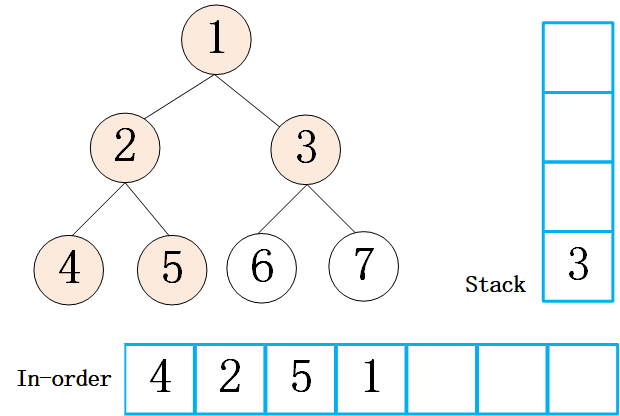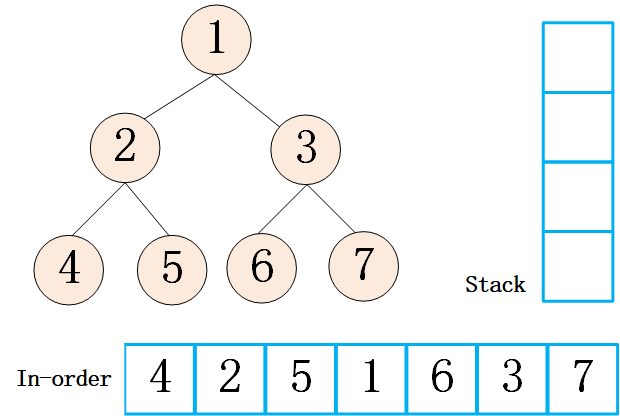
代码实现：
void inorder(TreeNode* root) {
// 节点是否为空
if (root == NULL) {
return;
}
stack<TreeNode*> inStack; // 存储节点
// 循环结束的条件是栈为空并且节点为空
while (!inStack.empty() || root != NULL) {
// 当节点不为空，向栈里添加左节点
if (root) {
inStack.push(root);
root = root->left;
}
else { // 节点为空，弹出栈顶元素作为根节点，打印，并查找其右节点
root = inStack.top();
cout << root->val << " ";
inStack.pop();
root = root->right;
}
}
cout << endl;
}
后序遍历
后序遍历，从左到右先遍历叶子后节点的方式遍历访问左右子树，最后访问根节点（左右根），如下图所示，是二叉树的后序遍历步骤，输出结果为 [4,7,8,5,2,6,3,1]。
递归的方法实现后序遍历，代码如下：
void recursionPostorder(TreeNode* root) {
if (root == NULL) {
return;
}
recursionPostorder(root->left);
recursionPostorder(root->right);
cout << root->val << " ";
}
同样的根据递归压榨的方法，这里需要一些技巧，先序遍历的时候是先压入右节点后压入左节点，这样栈弹出的顺序就是 “根左右”。后序遍历的顺序是 “左右根”，这样的话就需要两个栈，其中一个栈按照先压入左节点，再压入右节点的顺序，然后弹出后，存储到另一个栈中，变为 “根右左”，那么我们把整体的栈弹出以后，就变成了 “左右根”。上述过程用动画表示如下：
代码实现：
void postorder(TreeNode* root) {
// 根节点是否为空
if (root == NULL) {
return;
}
// 定义两个栈，用于数据存储，第一个栈调整数据，第二个栈用于后序遍历弹出
stack<TreeNode*> postStack1;
stack<TreeNode*> postStack2;
postStack1.push(root); // 把根节点压入第一个栈中
// 利用postStack1把所有数据压入postStack2中
while (!postStack1.empty()) {
root = postStack1.top();
postStack2.push(root);
postStack1.pop();
// 先压入左节点
if (root->left) {
postStack1.push(root->left);
}
// 后压入右节点
if (root->right) {
postStack1.push(root->right);
}
}
// 把postStack2弹出就是后序遍历
while (!postStack2.empty()) {
cout << postStack2.top()->val << " ";
postStack2.pop();
}
cout << endl;
}
欢迎大家关注我的个人公众号，同样的也是和该博客账号一样，专注分享技术问题，我们一起学习进步
