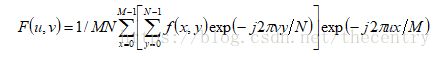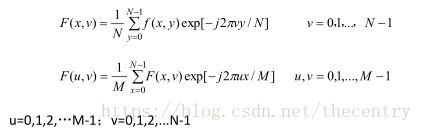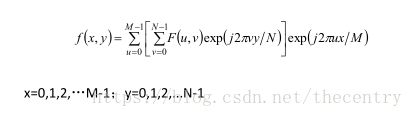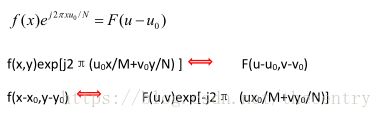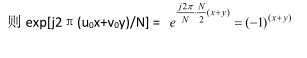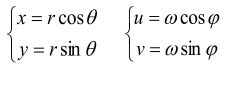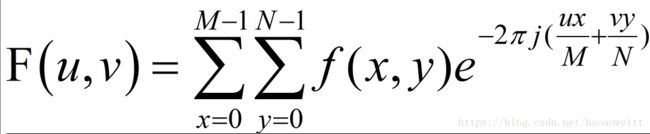MATALAB中的fft、fftshift相关原理说明

离散二维傅里叶变换原理说明：

一常用性质：

       可分离性、周期性和共轭对称性、平移性、旋转性质、卷积与相关定理；

（1）可分离性：

   二维离散傅里叶变换DFT可分离性的基本思想是DFT可分离为两次一维DFT。因此可以用通过计算两次一维的FFT来得到二维快速傅里叶FFT算法。根据快速傅里叶变换的计算要求，需要图像的行数、列数均满足2的n次方，如果不满足，在计算FFT之前先要对图像补零以满足2的n次。

   一个M行N列的二维图像f(x,y)，先按行队列变量y做一次长度为N的一维离散傅里叶变换，再将计算结果按列向对变量x做一次长度为M傅里叶变换就可以得到该图像的傅里叶变换结果，如式所示：

                      

将上式分解开来就是如下的两部分，先得到F(x,v),再由F(x,v)得到F(u,v)：

                        

 

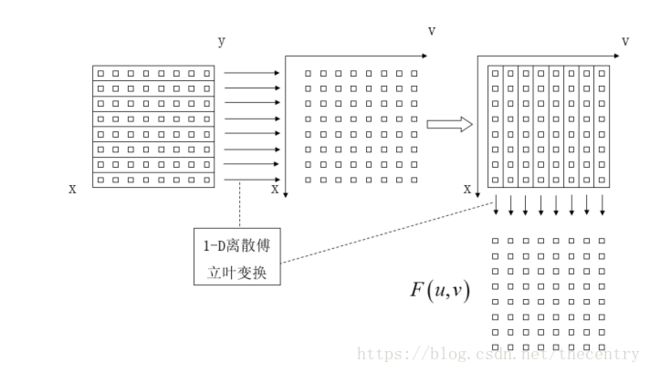
计算过程如下：

每一行由N个点，对每一行的一维N点序列进行离散傅里叶变换得到F(x,u),再对得到F(x,u)按列向对每一列做M点的离散傅里叶变换，就可以得到二维图像f(x,y)的离散傅里叶变换F(u,v).

同样，做傅里叶逆变换时，先对列向做一维傅里叶逆变换，再对行做一维逆傅里叶变换，如下式所示：

---

（2）周期性和共轭对称性

由傅里叶变换的基本性质可以知道，离散信号的频谱具有周期性。离散傅里叶变换DFT和它的里变换都以傅里叶变换的点数N为周期的。

对于一维傅里叶变换有：

对于二维傅里叶变换有：

类似有：即从DFT角度来看，反变换得到的图像阵列也是二维循环的。

共轭对称性

对于一维信号有：F(u)=F*(-u),如图所示的一维信号的幅度谱：点数为M的傅里叶变换一个周期为M，关于原点对称。原点即为0频率点，从图中可以看出在0频率的值最大，即信号f(x)的直流分量(均值)，远离原点处的即为高频成份，高频成份的幅值较小，说明信号的大部分能量集中在低频部分。

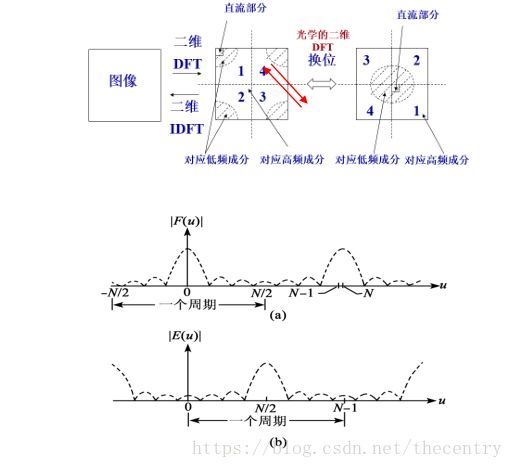
对于二维信号有：F(u,v)=F*(-u,-v)对于二维图像，其结果如图c所示。左上角(0,0)处为二维图像得0频率点，该点得值对应图像的平均灰度值，图中四个角对应低频成分，中间区域为高频成份，低频区域的幅度值打羽高频区域的幅度值，也同样表示该信号的主要能量集中在低频区域。

根据周期性和共轭对称性，在对图像进行频谱分析处理时只需要关注一个周期就可以了，同时利用图像的傅里叶变换和傅里叶变换的共轭可以直接计算图像的幅度谱，因此使得图像的频谱计算和显示得以简化。

（3)平移性：

傅里叶变换对有如下平移性质：

式子表明，

在频域中原点平移到(u0 ,v0)时，其对应的空间域 f(x,y)要乘上一个正的指数项：

                             

在空域中图像原点平移到(x0,y0)时，其对应的F(u,v)要乘上一个负的指数项：

                              

在数字图像处理中，常常需要将F(u,v)的原点移到N*N频域的中心，以便能清楚地分析傅里叶谱的情况，平移前空域、频域原点均在左上方。要做到这点，只需令上面平移公式中的：u0=v0=N/2；

所以

上式表明：如果需要将图像傅里叶谱的原点从左上角(0,0)移到中心点(N/2,N/2),只要f(x,y)乘上因子进行傅里叶变换即可实现。

平移性还体现了：当空域中f(x,y)产生移动时，在频域中只发生相移，并不影响他的傅里叶变换的幅度，因为：

                                        

反之，当频域中F(u,v)产生移动时，相应f(x,y)在空域中也只发生相移，不产生幅值变化。根据平移性质，为了更清楚查看二维图像的频谱，使直流成分出项在图像中央，在把画面分成四分的基础上，进行如图所示的换位(移位)也是可以的，这样，频域原点就回平移到中心。如下所示：

（4）旋转性质

 

如果 f(x,y)旋转了一个角度，那么 f(x,y)旋转后的图像的傅立叶变换也旋转了相同的角度。平面直角坐标改写成极坐标形式：

替换则有：

如果f(x,y)被旋转W,则F(u,v)被旋转同一角度。即有傅里叶变换对：

                            

 

如下所示：

 

同时，我们可以得出结论，对图像进行旋转变换和傅立叶变换的顺序是可交换的。即先旋转再傅里叶变换或者先傅里叶变换再旋转，得到的结果相同。F{R{f(x,y)}} = R{F{f(x,y)}}。

（5）卷积与相关定理

卷积定理包括空间域卷积和频率域卷积，卷积是空间域滤波和频率域滤波之间的纽带：两个空域信号的卷积等价于其频域信号的 乘积f(x,y)*h(x,y) → F(u,v)H(u,v) 或者 F{f(x,y)*h(x,y)} = F(u,v)H(u,v)；

两个信号频域上的卷积等价于空间域的相乘f(x,y) g(x,y) →F(u,v)*H(u,v)；

 

该性质的好处是将需要经过翻折、平移、相乘、求和等步骤实现的复杂的卷积运算简化为简单的乘法运算，这也是快速傅里叶变换（FFT）的出现使得该性质得到更广泛应用，同时，该性质对于理解信号的频率域处理方法特别重要，使得信号的空间域处理可以转换到频率域进行处理实现。

根据空间域卷积定理，在空间域对应的是原始信号与滤波器的冲击响应的卷积，卷积定义式为信号翻折平移求和的过程，步骤复杂，运算量大，但如果转换到频率域进行处理，则对在将二者的频谱直接相乘就可以得到滤波结果，然后对滤波结果进行傅里叶逆变换就可以得到滤波后的空间域域图像。如下图所示，对信号进行低通和高通滤波处理的过程和效果。

 

相关定理：

空域中 f(x,y)与 与 g(x,y) 的相关等价于频域中 F(u,v) 的共轭与 G(u,v)  相乘f(x,y) g(x,y) → F*(u,v)G(u,v)

同时有：f*(x,y)g(x,y) → F(u,v) G(u,v)

相关定理与卷积定理类似，也是把积分求和过程转化为了频域相乘，因此，也使得相关分析的计算简化。

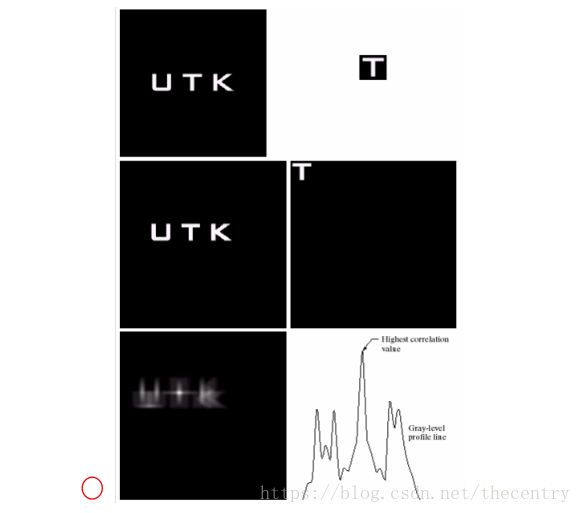
相关的重要应用在于匹配：确定是否有感兴趣的物体区域。f(x,y)是原始图像，g(x,y)作为感兴趣的物体或区域（模板），如果匹配，两个函数的相关值会在 f 中找到相应 g 点的位置上达到最大值。如下图所示。图像 f(x,y) 与模板 g(x,y)，通过计算相关函数，在匹配点处达到最大值，如图中红色圆圈标注的区域。

 

 

延拓图像 f(x,y)，延拓图像 g(x,y)，相关函数图像，通过相关图像最大值的水平灰度剖面图。

 

傅里叶变换的实例与应用

首先我们认识几点有关傅里叶变换的特点：

l 傅里叶变换是从将图像从空间域变换到频率域，具有明确的物理意义。图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度，在噪声点和图像边缘处的频率为高频。

l 在频率域中，将信号表示为一系列正弦信号或者复指数函数的叠加，正弦信号的频率、幅值和相位可以描述正弦信号中的所有信息，由此可以得到信号的幅度谱和相位谱。在图像领域就是将图像灰度作为正弦变量。

l 傅里叶变换全局性的，是一个积分求和的过程，对时间、地点位置无法进行准确定义，也就是说傅里叶变换得到的频谱图中的点无法与空间域中的某个空间位置对应，因此，从傅里叶变换图中并不能直接对应某个位置的特点。

l 傅里叶变换是一系列不同频率三角函数的和，每个频率分量的系数不同，这些系数代表了各频率成分的强弱或者所占比重，通过分析这些系数就可以分析图像的特性。

以上参考文献：

---

第二部分：matlab中fft和ifft

二维离散傅里叶变换的公式为：

 

                                                          

而后我们进行必要的数据测试，数据大小必须为2的幂次方：采用matlab

clc;
%创建一个待变换的二维矩阵
a=[1 1 3 5;
   1 1 1 1;
   1 1 2 1;
   1 1 1 1]
b=zeros(4);  %建立一个4*4j矩阵用于存储数据
temp = 0;
for r=1:4   %频率域成分
    for c=1:4 %频率域成分
        %下面两个是空间域成分，空间域的每一个值都对频谱有贡献
        for w=1:4
            for h=1:4
                temp=a(w,h)*exp(-2j*pi*((r-1)*(w-1)/4+(c-1)*(h-1)/4));
                b(r,c)= b(r,c)+temp;
            end
        end
        
    end
end
b
b1 = fft2(a)

 

运算结果：

而后我们测试fftshift，代码如下：

clc;
%创建一个待变换的二维矩阵
a=[1 1 3 5;
   1 1 1 1;
   1 1 2 1;
   1 1 1 1]
b=zeros(4);  %建立一个4*4j矩阵用于存储数据
temp = 0;
for r=1:4   %频率域成分
    for c=1:4 %频率域成分
        %下面两个是空间域成分，空间域的每一个值都对频谱有贡献
        for w=1:4
            for h=1:4
                temp=a(w,h)*exp(-2j*pi*((r-1)*(w-1)/4+(c-1)*(h-1)/4));
                b(r,c)= b(r,c)+temp;
            end
        end
        
    end
end
disp('FFT变换后的值：');
b
disp('MATLAB内部自带的程序FFT变换后的值：');
b1 = fft2(a)

disp('FFT变换后的DC分量移到正中心：');
b2= fftshift(b1)
disp('FFT反变换：');
%证明计算的结果完全一致
revrse_b2 = real(ifft2(ifftshift(b2)))

运行结果：前面第一部分是相同的。

测试证明，将fft之后的数据DC分量转换到坐标中心，经ifftshift之后得到的iff结果与原始数据完全一致。我们分析一下fftshift：

分析一下DC分量的中心，此时的实部最大，在分量中心向四周发散，相互对称的位置实部结果完全一致，虚部结果相反；共轭对称。

---

第三部分：matlab中的fftshift

根据第一部分傅里叶变化的周期性，共轭性，平移性质可以知道，在matlab中直接进行FFT变换得到的结果如下图所示：在数字图像处理中，常常需要将F(u,v)的原点移到N*N频域的中心，以便能清楚地分析傅里叶谱的情况，平移前空域、频域原点均在左上方。而fftshift的作用就是这样，将0频谱移到正中心。

接下来我们通过一个时间域离散信号的fft变换来说明fftshift在信号处理中的作用:

记信号f(t)的起始时间为t_start, 终止时间为t_end, 采样周期为t_s, 可以计算信号的持续时间Duration为 t_end – t_start, 信号离散化造成的采样点数 N = Duration/t_s + 1;

根据Fourier分析的相关结论，我们知道时域的采样将会造成频域的周期化，该周期为采样频率f_s（著名的香农采样定理基于此）.

%matlab fft 测试代码

t_s = 0.01;  %采样时间间隔，也就是周期0.01s,采集频率为100Hz
t_start = 0.5;  %起始时间
t_end = 5;     %终止时间
t = t_start:t_s:t_end; %时间序列
% 我们模拟了15Hz和45Hz的两种频率成分，正旋波
y = 0.5*sin(2*pi*15*t)+2*sin(2*pi*45*t);

y_f = fft(y);  %直接进行fft变换后的结果
subplot(3,1,1);
plot(t,y); title('original signal');

Duration = t_end - t_start;   %信号采集的持续时间
Sampling_points = Duration/t_s + 1; %采集的点数

f_s = 1/t_s;    %采样频率为周期的倒数，为100Hz
f_x = 0:f_s/Sampling_points:(Sampling_points-1)*f_s/Sampling_points;  %转换到频率域的序列

subplot(3,1,2);
plot(f_x,abs(y_f)); title('fft transform');

subplot(3,1,3);
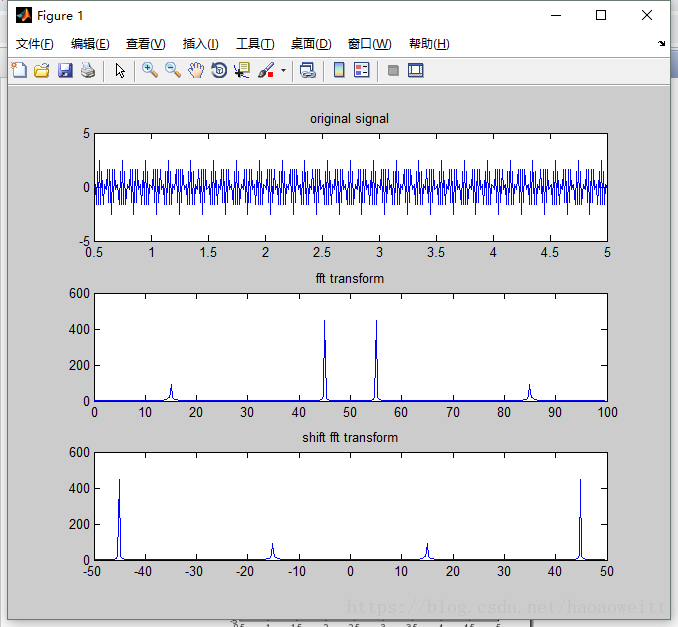
plot(f_x-f_s/2,abs(fftshift(y_f))); title('shift fft transform');

 

特别要注意横坐标的差别。另外，根据函数的特性，频谱应当只有在15Hz，45Hz出现峰值，但是fft变换后在55Hz，及85Hz处同样出现了峰值，应当可以从fft的计算过程中得到相应的解释。

事实上，如果我们用15Hz，60Hz来测试fft变换，也即是 y = 0.5*sin(2*pi*15*t)+2*sin(2*pi*55*t);图像如下所示，没有任何变化。

频率为100Hz，FFT变换后的频率成分包含15Hz，45Hz，55Hz（即100-45），85Hz（即100-15），后两种频率的出现是由于混叠效应，FFT解析的谱线与实际信号并不是一一对应的关系。

这种现象提醒我们，频率在f_s以内，即 0

实际上，这也就间接地证明了Nyquist采样定理的合理性：采样频率要高于截止频率的两倍，上面的处理中我们所使用的采样频率为100Hz，于是当截止频率超过50Hz时，就会出现混叠效应，特殊情况就如上图所示：完全一样。于是，这也就告诉我们若要正确的显示频谱，需要仔细地考量采样频率与截止频率的关系，若太小，则有可能出现混叠，若太大，则计算代价过高。

相关参考链接

参考网址：

https://blog.csdn.net/thecentry/article/details/80709593

https://blog.csdn.net/jialeheyeshu/article/details/51098348

https://blog.csdn.net/KatherineLOVER/article/details/72148008#%E5%8F%82%E8%80%83%E6%96%87%E7%8C%AE

推倒过程：https://blog.csdn.net/wind_desert/article/details/52989050

程序滤波C++：https://blog.csdn.net/Tuanz7/article/details/78261988