- 树状数组
- 1. 算法分析
- 2. 板子
- 2.1 一维树状数组:单点修改+区间查询
- 2.2 一维树状数组:区间修改+单点查询
- 2.3 一维树状数组:区间修改+区间查询
- 2.4 二维树状数组:单点修改+区间查询
- 2.5 二维树状数组:区间修改+单点查询
- 2.6 二维树状数组:区间修改+区间查询
- 3. 例题
- 3.1 树状数组+逆序对
- 3.2 树状数组+思维
- 3.3 树状数组6大基本模板+推公式变形
树状数组
1. 算法分析
树状数组作用
核心思想
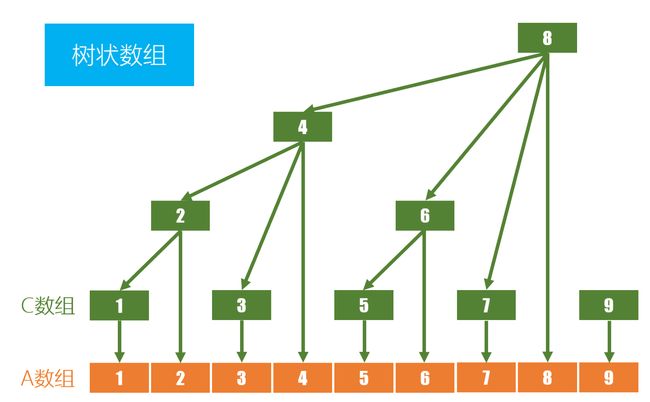
把前n个数划分为log(n)个区间,分别维护这log(n)个区间的和,在求解前缀和Sn的时候,从求解n个数字的和变成求解log(n)个区间的和来加快运算
具体操作
维护log(n)个区间,每个区间用数组c来维护区间和。单点修改x的时候,修改x所在的c,然后一路向上修改父节点的c;区间查询[1 ~ x]的时候,从x开始向前,把x的所有兄弟节点的c都加起来
c数组性质
- c[x]数组维护区间[x - lowbit(x) + 1, x]的和
- c[x]数组维护的区间的长度为lowbit(x)
- c[x]的父节点为 c[x + lowbit(x)]
- c[x]前一个兄弟节点为 c[x - lowbit(x)]
2. 板子
2.1 一维树状数组:单点修改+区间查询
#include
using namespace std;
typedef long long LL;
int const N = 5e5 + 10;
int a[N], n, m;
LL c[N], sum[N]; // c[x] = a[x-lowbit(x) + 1] + ... + a[x],sum[x]=a[1]+...+a[x]
int lowbit(int x) {
return x & (-x);
}
// 单点修改
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y; // 不断往父节点跳
}
// 查询Sx前缀和
LL query(int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i]; // 不断往前一个兄弟节点跳
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]); // 读入每个元素
sum[i] = sum[i - 1] + a[i]; // 计算前缀和
}
for (int i = 1; i <= n; ++i) c[i] = sum[i] - sum[i - lowbit(i)]; // 初始化c数组
for (int i = 1, op, x, y; i <= m; ++i) { // m个操作
scanf("%d%d%d", &op, &x, &y);
if (op == 1) add(x, y); // 单点修改
else printf("%lld\n", query(y) - query(x - 1)); // 区间查询
}
return 0;
}
2.2 一维树状数组:区间修改+单点查询
/*
本题要进行的是 区间增加+单点询问,而树状数组能进行的操作为 单点增加 + 区间查询
可以通过差分来实现这个转变,使得树状数组可以完成区间增加 + 单点询问
即:维护一个b数组表示当前a数组的增加减少情况,一旦a数组[l, r]增加d, 那么b[l] += d, b[r + 1] -= d
因此我们可以用树状数组维护这个b数组的前缀和,即维护一个c数组,记录b数组的前缀和,那么通过add()操作就能改变前缀和
而后每次询问单点时,我们查询b数组的前缀和就可以知道a点的增加减少情况
*/
#include
using namespace std;
typedef long long LL;
int n, m;
int const N = 1e5 + 10;
int c[N], a[N]; // c[x]维护的是b数组的前缀和
int lowbit(int x) {
return x & -x;
}
// 单点修改
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y; // 不断往父节点跳
}
// 查询Sx前缀和
LL query(int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i]; // 不断往前一个兄弟节点跳
return res;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); // 读入a[i]
while (m--) {
string op;
int l, r, d, x;
cin >> op;
// 单点查询
if (op[0] == 'Q') {
scanf("%d", &x);
printf("%lld\n", query(x) + a[x]); // x点的变化值+a[x]
}
else {
scanf("%d %d %d", &l, &r, &d);
add(l, d), add(r + 1, -d); // 区间增加
}
}
return 0;
}
2.3 一维树状数组:区间修改+区间查询
/*
对于第一种处理方式,可以利用差分结合acwing242一个简单的整数问题1的方式来处理;
对于问题而求区间和,那么考虑维护a的前缀和
a1+a2+...+ax=(b1)+(b1+b2)+(b1+b2+b3)+...+(b1+b2+b3+..+bx)
=(1+x)累加从1到x(bi)-累加从1到x(i*bi)
我们可以使用两个树状数组分别维护bi和i*bi的前缀和
*/
#include
using namespace std;
typedef long long LL;
int n, m;
int const N = 1e5 + 10;
LL c1[N], c2[N]; // c1维护bi的前缀和,c2维护i*bi的前缀和
int a[N];
LL s[N];
int lowbit(int x) {
return x & -x;
}
// 单点修改
void add(LL c[], int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += (LL)y;
}
// 前缀和
LL query(LL c[], int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
s[i] = s[i - 1] + 0ll + a[i]; // 计算原来的a[i]的前缀和
}
while (m--) {
string op;
int l, r, d;
cin >> op;
if (op[0] == 'C') {
cin >> l >> r >> d;
add(c1, l, d), add(c1, r + 1, -d); // 把[l, r]加d对c1来说就是把l和r+1分别增加d和减去d
add(c2, l, l * d), add(c2, r + 1, -(r + 1) * d); // 把[l, r]加d对c1来说就是把l和r+1分别增加l*d和减去(r+1)*d
}
else {
cin >> l >> r;
LL res = s[r] - s[l - 1]; // 原来的区间和
res += ((1 + r) * query(c1, r) - query(c2, r) - (l * query(c1, l - 1) - query(c2, l - 1))); // 加上改变值
printf("%lld\n", res );
}
}
return 0;
}
2.4 二维树状数组:单点修改+区间查询
#include
using namespace std;
typedef long long LL;
int const N = (1 << 12) + 10;
LL n, m, c[N][N]; // c[x][y] = 累加c[i][j], i∈(i-lowbit(i)+1, x), j∈(j-lowbit(j)+1, y)
int lowbit(int x) {
return x & -x;
}
// 单点修改
void add(int x, int y, int z) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
c[i][j] += (LL)z;
}
// 区间查询
LL query(int x, int y) {
LL res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += c[i][j];
return res;
}
int main() {
cin >> n >> m;
int op, x1, y1, k, x2, y2;
while (scanf("%d", &op) != EOF) {
if (op == 1) { // 单点修改,把(x1, y1)加上k
scanf("%d%d%d", &x1, &y1, &k);
add(x1, y1, k);
}
else { // 区间查询,得到以左上角为(x1, y1),右下角为(x2, y2)的矩形的区间和
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%lld\n", query(x2, y2) - query(x2, y1 - 1) - query(x1 - 1, y2) + query(x1 - 1, y1 - 1));
}
}
return 0;
}
2.5 二维树状数组:区间修改+单点查询
#include
using namespace std;
typedef long long LL;
int const N = (1 << 12) + 10;
LL c[N][N], n, m, op; // c[x][y]维护b[i][j]的前缀和
int lowbit(int x) {
return x & (-x);
}
// 二维单点修改
void add(int x, int y, int z) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
c[i][j] += z;
}
// 求二维前缀和
LL query(int x, int y) {
LL res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += c[i][j];
return res;
}
int main() {
cin >> n >> m;
while (scanf("%lld", &op) != EOF) {
int x1, y1, k, x2, y2;
if (op == 1) { // 区间增加:转化为二维差分数组的增加
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, & k);
add(x2 + 1, y2 + 1, k);
add(x1, y1, k);
add(x2 + 1, y1, -k);
add(x1, y2 + 1, -k);
}
else { // 单点查询:转化为二维差分数组求前缀和
scanf("%d%d", &x1, &y1);
printf("%lld\n", query(x1, y1));
}
}
return 0;
}
2.6 二维树状数组:区间修改+区间查询
/*
累加aij(i∈[1, x], j∈[1, y])=(x+1)*(y+1)累加bij - (x+1)累加j*bij - (y + 1)累加i*bij + 累加i*j*bij
c1维护bij的二维前缀和,c2维护j*bij的二维前缀和,c3维护i*bij的二维前缀和,c4维护i*j*bij的二维前缀和
*/
#include
using namespace std;
typedef long long LL;
int const N = (1 << 12) + 10;
LL c1[N][N], c2[N][N], c3[N][N], c4[N][N], n, m, op; // c[x][y]维护b[i][j]的前缀和
int lowbit(int x) {
return x & (-x);
}
// 二维单点修改
void add(LL c[][N], int x, int y, LL z) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
c[i][j] += z;
}
// 求二维前缀和
LL query(LL c[][N], int x, int y) {
LL res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += c[i][j];
return res;
}
LL Query(int x, int y) {
return (x + 1) * (y + 1) * query(c1, x, y) - (x + 1) * query(c2, x, y) - (y + 1) * query(c3, x, y) + query(c4, x, y);
}
int main() {
cin >> n >> m;
while (scanf("%lld", &op) != EOF) {
int x1, y1, x2, y2, k;
if (op == 1) {
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &k);
add(c1, x2 + 1, y2 + 1, k), add(c1, x1, y1, k), add(c1, x2 + 1, y1, -k), add(c1, x1, y2 + 1, -k);
add(c2, x2 + 1, y2 + 1, k * (y2 + 1)), add(c2, x1, y1, k * y1), add(c2, x2 + 1, y1, -k * y1), add(c2, x1, y2 + 1, -k * (y2 + 1));
add(c3, x2 + 1, y2 + 1, k * (x2 + 1)), add(c3, x1, y1, k * x1), add(c3, x2 + 1, y1, -k * (x2 + 1)), add(c3, x1, y2 + 1, -k * x1);
add(c4, x2 + 1, y2 + 1, k * (x2 + 1) * (y2 + 1)), add(c4, x1, y1, k * x1 * y1), add(c4, x2 + 1, y1, -k * (x2 + 1) * y1), add(c4, x1, y2 + 1, -k * x1 * (y2 + 1));
}
else {
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%lld\n", Query(x2, y2) + Query(x1 - 1, y1 - 1) - Query(x1 - 1, y2) - Query(x2, y1 - 1));
}
}
return 0;
}
3. 例题
3.1 树状数组+逆序对
POJ2299 Ultra-QuickSort
有多个测试样例,每个测试样例给定n个数字a[i], 求这n个数字的逆序对数目
n~5e5, a[i]~999999999
// 使用树状数组去维护每个数字出现的次数的前缀和,c[i]记录i这个节点管辖的几个点的出现次数
// 统计时,只要统计每个点右边有多少个比他小即可
// 注意需要离散化
#include
using namespace std;
typedef long long LL;
int const N = 5e5 + 10;
LL c[N], n, a[N];
vector v;
unordered_map H;
int lowbit(int x) {
return x & -x;
}
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
LL query(int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
while (scanf("%lld", &n) != EOF && n) {
memset(c, 0, sizeof c);
v.clear();
H.clear();
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
v.push_back(a[i]);
}
sort(v.begin(), v.end());
int cnt = 1;
for (int i = 0; i < v.size(); ++i) H[v[i]] = cnt++; // 离散化
LL res = 0;
for (int i = n; i >= 1; --i) { // 计算每个H[a[i]出现的次数
res += query(H[a[i]] - 1); // 加上H[a[i]-1出现的总次数
add(H[a[i]], 1); // 次数加一
}
printf("%lld\n", res);
}
return 0;
}
acwing241楼兰图腾
有n个点,坐标分别为(1, y1), (2, y2), (3, y3), ..., (n, yn)
如果三个点(i, yi), (j, yj), (k, yk) 满足1 ≤ i < j < k ≤ n且yi > yj, yj < yk,则称这三个点构成V图腾;
如果三个点(i, yi), (j, yj), (k, yk)满足1 ≤ i < j < k ≤ n 且yi < yj, yj > yk,则称这三个点构成∧图腾;
求有多少个V图腾和∧图腾
n ~ 2e5, yi ~ 2e5
/*
使用树状数组去维护每个数字出现的次数的前缀和,c[i]记录i这个节点管辖的几个点的出现次数
统计时,只要统计每个点左边有多少个比他大,右边有多少个比他大,然后相乘就能够知道出现多少个^;
统计V则相反
*/
#include
using namespace std;
typedef long long LL;
int n;
int const N = 2e5 + 10;
int a[N], c[N];
int gre[N], low[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
cin >> n;
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
LL res1 = 0, res2 = 0;
for (int i = 0; i < n; ++i) {
int y = a[i];
gre[i] = query(n) - query(y);
low[i] = query(y - 1);
add(y , 1);
}
memset(c, 0, sizeof c);
for (int i = n - 1; i >= 0; --i) {
int y = a[i];
res1 += (LL)gre[i] * (query(n) - query(y));
res2 += (LL)low[i] * query(y - 1);
add(y , 1);
}
cout << res1 << " " << res2 << endl;
return 0;
}
POJ3067 Japan
有两个海岸,两个海岸分别有N个点和M个点,从北到南编号为1,2,3...,N。现在在两个海岸之间建设桥梁。每个桥梁给出x, y,表示第一个海岸的x点到第二个海岸的y点有桥梁。问形成交叉的桥梁数目有多少。
N、M~1e3
// 设桥梁1为(x1, y1),桥梁2为(x2, y2),当(x1-x2)*(y1-y2)<0时两个桥梁交叉
// 因此只需要把y按照从大到小的顺序排序,每次观察小于当前x的数有多少个即可
// 这样就转化为求解逆序对的问题,树状数组求之
#include
using namespace std;
typedef long long LL;
int n, m, T, q, kase = 1;
int const N = 1e3 + 10;
LL c[N];
struct Line {
int x, y;
bool operator<(const struct Line &w) const {
if (y == w.y) return x > w.x;
else return y > w.y;
}
}line[N * N];
LL lowbit(LL x) {
return x & -x;
}
// 单点修改
void add(int x, LL y) {
for (int i = x; i <= N; i += lowbit(i)) c[i] += y; // 不断往父节点跳
}
// 查询Sx前缀和
LL query(int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i]; // 不断往前一个兄弟节点跳
return res;
}
int main()
{
cin >> T;
while (T--) {
cin >> n >> m >> q;
memset(c, 0, sizeof c);
for (int i = 1; i <= q; ++i) scanf("%d%d", &line[i].x, &line[i].y);
sort(line + 1, line + 1 + q); // 按y从大到小排序
LL res = 0;
for (int i = 1; i <= q; ++i) {
res += query(line[i].x - 1); // 计算小于当前x的数目
add(line[i].x, 1); // 当前x加一
}
printf("Test case %d: %lld\n", kase++, res);
}
return 0;
}
POJ 2352 Stars
给一个二维网格,然后给定网格上n个点,计算每个点的左下方的点个数
点的输入是y从小到大输入,如果y相同,那么x从小到大输入。
n~15000, x、y~32000
// 题目顺序都处理好了。注意向右平移一个单位,因为0号位置也有star
#include
using namespace std;
typedef long long LL;
int const N = 2e5 + 10;
int n;
LL c[N], res[N];
int lowbit(int x) {
return x & (-x);
}
// 单点修改
void add(int x, int y) {
for (int i = x; i <= N; i += lowbit(i)) c[i] += y; // 不断往父节点跳
}
// 查询Sx前缀和
LL query(int x) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i]; // 不断往前一个兄弟节点跳
return res;
}
int main() {
cin >> n;
for (int i = 1, x, y; i <= n; ++i) {
scanf("%d%d", &x, &y);
x++; // 树状数组不能统计0
res[query(x)]++; // 计数
add(x, 1); //x的次数加一
}
for (int i = 0; i <= n - 1; ++i) printf("%lld\n", res[i]);
return 0;
}
3.2 树状数组+思维
acwing244谜一样的牛
有n头奶牛,已知它们的身高为 1~n 且各不相同,但不知道每头奶牛的具体身高。
现在这n头奶牛站成一列,已知第i头牛前面有Ai头牛比它低,求每头奶牛的身高。
1≤n≤105
/*
本题可以从n往1向前看,如果他的前面有a[i]头牛比他低,那第i头牛的高度就是可以选择的身高的第i+1小。
因此可以给每个身高一个标值,1表示没被选,0表示被选中。那么寻找第a[i]+1个没被选中的牛就可以二分查找
前缀和等于a[i]+1的那个数字,树状数组维护这个前缀和即可
*/
#include
using namespace std;
int n;
int const N = 1e5 + 10;
int c[N], a[N], ans[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main()
{
cin >> n;
for (int i = 2; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) c[i] = lowbit(i); // 初始化,因为每个身高都没备选,那么都初始化为1,Tr数组就是区间的长度,即为lowbit(i)
for (int i = n; i >= 1; --i) // 倒着往前看
{
// 二分查找a[i]+1小
int l = 1, r = n;
while (l < r)
{
int mid = (l + r) >> 1;
if (query(mid) >= a[i] + 1) r = mid;
else l = mid + 1;
}
ans[i] = l; // 记录答案
add(l, -1); // 这个牛被选了,从1变成0
}
for (int i = 1; i <= n; ++i) printf("%d\n", ans[i]);
return 0;
}
acwing260买票
给定n,表示游客的数目;随后n行,每行两个数,p[i]和v[i],分别表示当这个游客插队后,前面的人数以及这个游客的编号。求出当全部游客完成插队后,队列中的游客编号情况。
n ~ 2e5,P[i]、V[i] ~ short
// 本题的思路和acwing244一样,倒着往前看,插入前面人数+1的位置。
#include
using namespace std;
int const N = 2e5 + 10;
int res[N], P[N], V[N], n, c[N];
typedef long long LL;
int lowbit(int x) {
return x & -x;
}
void add(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &P[i], &V[i]);
c[i] = lowbit(i);
}
for (int i = n; i >= 1; --i) {
int pos = P[i] + 1;
int l = 1, r = n;
while (l < r) {
int mid = l + r >> 1;
if (query(mid) >= pos) r = mid;
else l = mid + 1;
}
res[l] = V[i];
add(l, -1);
}
for (int i = 1; i <= n; ++i) printf("%d ", res[i]);
cout << endl;
}
return 0;
}
Vijos P1448校门外的树
校门外有很多树,有苹果树,香蕉树,有会扔石头的,有可以吃掉补充体力的……如今学校决定在某个时刻在某一段种上一种树,保证任一时刻不会出现两段相同种类的树,现有两个操作:
K=1,读入l、r表示在区间[l,r]中种上一种树,每次操作种的树的种类都不同
K=2,读入l,r表示询问l~r之间能见到多少种树
(l,r>0)
校门长度n,询问次数m<=50000
/* 左右括号的方法。在一个区间内种树,相当于加一对括号。用树状数组维护从起始到这个位置的左右括号的数量。
区间内有左括号那么一定有这一种类型的树,只有离开了对应的右括号这种树才没有了。
所以为了统计区间[x,y]内的树种类,只需把y左边左括号的个数-(x-1)左边右括号的个数即可。 */
#include
using namespace std;
int const N = 5e4 + 10;
int c1[N], c2[N], n, m; // c1[x]维护左括号的数目,c2[x]维护右括号的数目
int lowbit(int x) {
return x & -x;
}
void add(int c[], int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}
int query(int c[], int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
cin >> n >> m;
for (int i = 1, op, l, r; i <= m; ++i) {
scanf("%d%d%d", &op, &l, &r);
if (op == 1) add(c1, l, 1), add(c2, r, 1); // l处左括号数目加一,r处右括号数目加一
else printf("%d\n", query(c1, r) - query(c2, l - 1)); // r的左括号数目-(l-1)的右括号数目
}
return 0;
}
POJ2155 Matrix
一个n*n的只含01二维矩阵,有m个操作,每个操作两种类型:
C x1 y1 x2 y2:把以(x1, y1)为左上角,(x2, y2)为右下角的矩阵的内的数全部反转(0变1,1变0)
Q x y:查询a[x][y]的数是多少
n、m~1e5
// 翻转一个区间相当于区间的每个数加1,最后是0还是1就模2即可。
// 加1在模2的意义下就是把01反转
#include
using namespace std;
typedef long long LL;
int const N = 1e3 + 10;
LL c[N][N], n, m, op, T; // c[x][y]维护b[i][j]的前缀和
int lowbit(int x) {
return x & (-x);
}
void add(int x, int y, LL z) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= n; j += lowbit(j))
c[i][j] += z;
}
LL query(int x, int y) {
LL res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += c[i][j];
return res;
}
int main() {
cin >> T;
while (T--) {
memset(c, 0, sizeof c);
cin >> n >> m;
for (int i = 1, x1, y1, x2, y2; i <= m; ++i) {
char op[2];
scanf("%s", op);
if (op[0] == 'C') { // 区间增加1
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
add(x2 + 1, y2 + 1, 1);
add(x1, y1, 1);
add(x2 + 1, y1, -1);
add(x1, y2 + 1, -1);
}
else { // 单点查询
scanf("%d%d", &x1, &y1);
printf("%lld\n", query(x1, y1) % 2);
}
}
printf("\n");
}
return 0;
}
3.3 树状数组6大基本模板+推公式变形
ACM-ICPC 2018 徐州赛区网络预赛 H.Ryuji doesn't want to study
一开始给定n个数,m次询问。每次询问两种类型:
1 x y, 表示询问a[l]*len + a[l + 1] * (len - 1) + ... + a[r] * 1,len = r - l + 1。
2 x y, 表示把a[x]赋值为y
n ~ 1e5, m ~ 1e5
题解:\(\sum_{i=l}^ra[i]*(r - i + 1) = (r+1)\sum_{i=l}^ra[i] - \sum_{i=l}^ri * a[i]\)
因此,可以使用树状数组分别维护a[i]和i * a[i]的前缀和即可
#include
using namespace std;
typedef long long LL;
int n, m;
int const N = 1e5 + 10;
LL c1[N], c2[N], a[N], sum1[N], sum2[N]; // c1[x]维护ai的前缀和,c2[x]维护i*ai的前缀和
LL lowbit(LL x) {
return x & -x;
}
// 单点修改
void add(LL c[], int x, LL y) {
for (int i = x; i <= n; i += lowbit(i)) c[i] += y; // 不断往父节点跳
}
// 查询Sx前缀和
LL query(int x, LL c[]) {
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i]; // 不断往前一个兄弟节点跳
return res;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]); // 读入a[i]
sum1[i] = sum1[i - 1] + a[i];
sum2[i] = sum2[i - 1] + i * a[i];
}
for (int i = 1; i <= n; ++i) {
c1[i] = sum1[i] - sum1[i - lowbit(i)];
c2[i] = sum2[i] - sum2[i - lowbit(i)];
}
while (m--) {
LL op, x, y;
scanf("%lld%lld%lld", &op, &x, &y);
if (op == 1) { // 询问
printf("%lld\n", (y + 1) * (query(y, c1) - query(x - 1, c1)) - (query(y, c2) - query(x - 1, c2)));
}
else { // 单点修改
add(c1, x, y - a[x]), add(c2, x, x * y - x * a[x]);
a[x] = y;
}
}
return 0;
}