总结 离散数学知识点
总结 离散数学知识点
第二章 命题逻辑
1.→,前键为真,后键为假才为假;<—>,相同为真,不同为假;
2.主析取范式:极小项(m)之和;主合取范式:极大项(M)之积;
3.求极小项时,命题变元的肯定为1,否定为0,求极大项时相反;
4.求极大极小项时,每个变元或变元的否定只能出现一次,求极小项时变元不够合取真,求极大项时变元不够析取假;
5.求范式时,为保证编码不错,命题变元最好按P,Q,R的顺序依次写;
6.真值表中值为1的项为极小项,值为0的项为极大项;
7.n个变元共有个极小项或极大项,这为(0~-1)刚好为化简完后的主析取加主合取;
8.永真式没有主合取范式,永假式没有主析取范式;
9.推证蕴含式的方法(=>):真值表法;分析法(假定前键为真推出后键为真,假定前键为假推出后键也为假)
10.命题逻辑的推理演算方法:P规则,T规则
①真值表法;②直接证法;③归谬法;④附加前提法;
第三章 谓词逻辑
1.一元谓词:谓词只有一个个体,一元谓词描述命题的性质;
多元谓词:谓词有n个个体,多元谓词描述个体之间的关系;
2.全称量词用蕴含→,存在量词用合取^;
3.既有存在又有全称量词时,先消存在量词,再消全称量词;
第四章 集合
1.N,表示自然数集,1,2,3……,不包括0;
2.基:集合A中不同元素的个数,|A|;
3.幂集:给定集合A,以集合A的所有子集为元素组成的集合,P(A);
4.若集合A有n个元素,幂集P(A)有个元素,|P(A)|==;
5.集合的分划:(等价关系)
①每一个分划都是由集合A的几个子集构成的集合;
②这几个子集相交为空,相并为全(A);
6.集合的分划与覆盖的比较:
分划:每个元素均应出现且仅出现一次在子集中;
覆盖:只要求每个元素都出现,没有要求只出现一次;
第五章 关系
1.若集合A有m个元素,集合B有n个元素,则笛卡尔A×B的基数为mn,A到B上可以定义种不同的关系;
2.若集合A有n个元素,则|A×A|=,A上有个不同的关系;
3.全关系的性质:自反性,对称性,传递性;
空关系的性质:反自反性,反对称性,传递性;
全封闭环的性质:自反性,对称性,反对称性,传递性;
4.前域(domR):所有元素x组成的集合;
后域(ranR):所有元素y组成的集合;
5.自反闭包:r(R)=RU;
对称闭包:s(R)=RU;
传递闭包:t(R)=RUUU……
6.等价关系:集合A上的二元关系R满足自反性,对称性和传递性,则R称为等价关系;
7.偏序关系:集合A上的关系R满足自反性,反对称性和传递性,则称R是A上的一个偏序关系;
8.covA={
9.极小元:集合A中没有比它更小的元素(若存在可能不唯一);
极大元:集合A中没有比它更大的元素(若存在可能不唯一);
最小元:比集合A中任何其他元素都小(若存在就一定唯一);
最大元:比集合A中任何其他元素都大(若存在就一定唯一);
10.前提:B是A的子集
上界:A中的某个元素比B中任意元素都大,称这个元素是B的上界(若存在,可能不唯一);
下界:A中的某个元素比B中任意元素都小,称这个元素是B的下界(若存在,可能不唯一);
上确界:最小的上界(若存在就一定唯一);
下确界:最大的下界(若存在就一定唯一);
第六章 函数
1.若|X|=m,|Y|=n,则从X到Y有种不同的关系,有种不同的函数;
2.在一个有n个元素的集合上,可以有种不同的关系,有种不同的函数,有n!种不同的双射;
3.若|X|=m,|Y|=n,且m<=n,则从X到Y有种不同的单射;
4.单射:f:X-Y,对任意,属于X,且≠,若f()≠f();
满射:f:X-Y,对值域中任意一个元素y在前域中都有一个或多个元素对应;
双射:f:X-Y,若f既是单射又是满射,则f是双射;
5.复合函数:fºg=g(f(x));
6.设函数f:A-B,g:B-C,那么
①如果f,g都是单射,则fºg也是单射;
②如果f,g都是满射,则fºg也是满射;
③如果f,g都是双射,则fºg也是双射;
④如果fºg是双射,则f是单射,g是满射;
第七章 代数系统
1.二元运算:集合A上的二元运算就是到A的映射;
2. 集合A上可定义的二元运算个数就是从A×A到A上的映射的个数,即从从A×A到A上函数的个数,若|A|=2,则集合A上的二元运算的个数为==16种;
3. 判断二元运算的性质方法:
①封闭性:运算表内只有所给元素;
②交换律:主对角线两边元素对称相等;
③幂等律:主对角线上每个元素与所在行列表头元素相同;
④有幺元:元素所对应的行和列的元素依次与运算表的行和列相同;
⑤有零元:元素所对应的行和列的元素都与该元素相同;
4.同态映射:
第八章 群
1.广群的性质:封闭性;
半群的性质:封闭性,结合律;
含幺半群(独异点):封闭性,结合律,有幺元;
群的性质:封闭性,结合律,有幺元,有逆元;
2.群没有零元;
3.阿贝尔群(交换群):封闭性,结合律,有幺元,有逆元,交换律;
4.循环群中幺元不能是生成元;
5.任何一个循环群必定是阿贝尔群;
第十章 格与布尔代数
1.格:偏序集合A中任意两个元素都有上、下确界;
2.格的基本性质:
1) 自反性
a≤a 对偶: a≥a
2) 反对称性
a≤b ^ b≥a => a=b
对偶:a≥b ^ b≤a => a=b
3) 传递性
a≤b ^ b≤c => a≤c
对偶:a≥b ^ b≥c => a≥c
4) 最大下界描述之一
a^b≤a 对偶 avb≥a
A^b≤b 对偶 avb≥b
5)最大下界描述之二
c≤a,c≤b => c≤a^b
对偶c≥a,c≥b =>Þc≥avb
6) 结合律
a^(b^c)=(a^b)^c
对偶 av(bvc)=(avb)vc
7) 等幂律
a^a=a 对偶 ava=a
8) 吸收律
a^(avb)=a 对偶 av(a^b)=a
9) a≤b <=> a^b=a avb=b
10) a≤c,b≤d => a^b≤c^d avb≤cvd
11) 保序性
b≤c => a^b≤a^c avb≤avc
12) 分配不等式
av(b^c)≤(avb)^(avc)
对偶 a^(bvc)≥(a^b)v(a^c)
13)模不等式
a≤c <=>Û av(b^c)≤(avb)^c
3.分配格:满足a^(bvc)=(a^b)v(a^c)和av(b^c)=(avb)^(avc);
4.分配格的充要条件:该格没有任何子格与钻石格或五环格同构;
5.链格一定是分配格,分配格必定是模格;
6.全上界:集合A中的某个元素a大于等于该集合中的任何元素,则称a为格
全下界:集合A中的某个元素b小于等于该集合中的任何元素,则称b为格
7.有界格:有全上界和全下界的格称为有界格,即有0和1的格;
8.补元:在有界格内,如果a^b=0,avb=1,则a和b互为补元;
9.有补格:在有界格内,每个元素都至少有一个补元;
10.有补分配格(布尔格):既是有补格,又是分配格;
11.布尔代数:一个有补分配格称为布尔代数;
第十一章 图论
1.邻接:两点之间有边连接,则点与点邻接;
2.关联:两点之间有边连接,则这两点与边关联;
3.平凡图:只有一个孤立点构成的图;
4.简单图:不含平行边和环的图;
5.无向完全图:n个节点任意两个节点之间都有边相连的简单无向图;
有向完全图:n个节点任意两个节点之间都有边相连的简单有向图;
6.无向完全图有n(n-1)/2条边,有向完全图有n(n-1)条边;
7.r-正则图:每个节点度数均为r的图;
8.握手定理:节点度数的总和等于边的两倍;
9.任何图中,度数为奇数的节点个数必定是偶数个;
10.任何有向图中,所有节点入度之和等于所有节点的出度之和;
11.每个节点的度数至少为2的图必定包含一条回路;
12.可达:对于图中的两个节点,,若存在连接到的路,则称与相互可达,也称与是连通的;在有向图中,若存在到的路,则称到可达;
13.强连通:有向图章任意两节点相互可达;
单向连通:图中两节点至少有一个方向可达;
弱连通:无向图的连通;(弱连通必定是单向连通)
14.点割集:删去图中的某些点后所得的子图不连通了,如果删去其他几个点后子图之间仍是连通的,则这些点组成的集合称为点割集;
割点:如果一个点构成点割集,即删去图中的一个点后所得子图是不连通的,则该点称为割点;
15.关联矩阵:M(G),是与关联的次数,节点为行,边为列;
无向图:点与边无关系关联数为0,有关系为1,有环为2;
有向图:点与边无关系关联数为0,有关系起点为1终点为-1,
关联矩阵的特点:
无向图:
①行:每个节点关联的边,即节点的度;
②列:每条边关联的节点;
有向图:
③所有的入度(1)=所有的出度(0);
16.邻接矩阵:A(G),是邻接到的边的数目,点为行,点为列;
17.可达矩阵:P(G),至少存在一条回路的矩阵,点为行,点为列;
P(G)=A(G)+(G)+(G)+(G)
可达矩阵的特点:表明图中任意两节点之间是否至少存在一条路,以及在任何节点上是否存在回路;
A(G)中所有数的和:表示图中路径长度为1的通路条数;
(G)中所有数的和:表示图中路径长度为2的通路条数;
(G)中所有数的和:表示图中路径长度为3的通路条数;
(G)中所有数的和:表示图中路径长度为4的通路条数;
P(G)中主对角线所有数的和:表示图中的回路条数;
18.布尔矩阵:B(G),到有路为1,无路则为0,点为行,点为列;
19.代价矩阵:邻接矩阵元素为1的用权值表示,为0的用无穷大表示,节点自身到自身的权值为0;
20.生成树:只访问每个节点一次,经过的节点和边构成的子图;
21.构造生成树的两种方法:深度优先;广度优先;
深度优先:
①选定起始点;
②选择一个与邻接且未被访问过的节点;
③从出发按邻接方向继续访问,当遇到一个节点所有邻接点均已被访问时,回到该节点的前一个点,再寻求未被访问过的邻接点,直到所有节点都被访问过一次;
广度优先:
①选定起始点;
②访问与邻接的所有节点,,……,,这些作为第一层节点;
③在第一层节点中选定一个节点为起点;
④重复②③,直到所有节点都被访问过一次;
22.最小生成树:具有最小权值(T)的生成树;
23.构造最小生成树的三种方法:
克鲁斯卡尔方法;管梅谷算法;普利姆算法;
(1)克鲁斯卡尔方法
①将所有权值按从小到大排列;
②先画权值最小的边,然后去掉其边值;重新按小到大排序;
③再画权值最小的边,若最小的边有几条相同的,选择时要满足不能出现回路,然后去掉其边值;重新按小到大排序;
④重复③,直到所有节点都被访问过一次;
(2)管梅谷算法(破圈法)
①在图中取一回路,去掉回路中最大权值的边得一子图;
②在子图中再取一回路,去掉回路中最大权值的边再得一子图;
③重复②,直到所有节点都被访问过一次;
(3)普利姆算法
①在图中任取一点为起点,连接边值最小的邻接点;
②以邻接点为起点,找到邻接的最小边值,如果最小边值比邻接的所有边值都小(除已连接的边值),直接连接,否则退回,连接现在的最小边值(除已连接的边值);
③重复操作,直到所有节点都被访问过一次;
24.关键路径
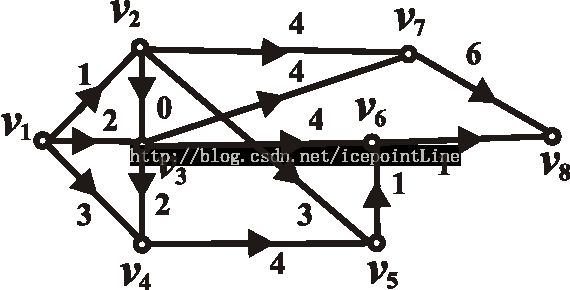
例2 求PERT图中各顶点的最早完成时间, 最晚完成时间, 缓冲时间及关键路径.
解:最早完成时间
TE(v1)=0
TE(v2)=max{0+1}=1
TE(v3)=max{0+2,1+0}=2
TE(v4)=max{0+3,2+2}=4
TE(v5)=max{1+3,4+4}=8
TE(v6)=max{2+4,8+1}=9
TE(v7)=max{1+4,2+4}=6
TE(v8)=max{9+1,6+6}=12
最晚完成时间
TL(v8)=12
TL(v7)=min{12-6}=6
TL(v6)=min{12-1}=11
TL(v5)=min{11-1}=10
TL(v4)=min{10-4}=6
TL(v3)=min{6-2,11-4,6-4}=2
TL(v2)=min{2-0,10-3,6-4}=2
TL(v1)=min{2-1,2-2,6-3}=0
缓冲时间
TS(v1)=0-0=0
TS(v2)=2-1=1
TS(v3)=2-2=0
TS(v4)=6-4=2
TS(v5=10-8=2
TS(v6)=11-9=2
TS(v7)=6-6=0
TS(v8)=12-12=0
关键路径: v1-v3-v7-v8
25.欧拉路:经过图中每条边一次且仅一次的通路;
欧拉回路:经过图中每条边一次且仅一次的回路;
欧拉图:具有欧拉回路的图;
单向欧拉路:经过有向图中每条边一次且仅一次的单向路;
欧拉单向回路:经过有向图中每条边一次且仅一次的单向回路;
26.(1)无向图中存在欧拉路的充要条件:
①连通图;②有0个或2个奇数度节点;
(2)无向图中存在欧拉回路的充要条件:
①连通图;②所有节点度数均为偶数;
(3)连通有向图含有单向欧拉路的充要条件:
①除两个节点外,每个节点入度=出度;
②这两个节点中,一个节点的入度比出度多1,另一个节点的入;度比出度少1;
(4)连通有向图含有单向欧拉回路的充要条件:
图中每个节点的出度=入度;
27.哈密顿路:经过图中每个节点一次且仅一次的通路;
哈密顿回路:经过图中每个节点一次且仅一次的回路;
哈密顿图:具有哈密顿回路的图;
28.判定哈密顿图(没有充要条件)
必要条件:
任意去掉图中n个节点及关联的边后,得到的分图数目小于等于n;
充分条件:
图中每一对节点的度数之和都大于等于图中的总节点数;
29.哈密顿图的应用:安排圆桌会议;
方法:将每一个人看做一个节点,将每个人与和他能交流的人连接,找到一条经过每个节点一次且仅一次的回路(哈密顿图),即可;
30.平面图:将图形的交叉边进行改造后,不会出现边的交叉,则是平面图;
31.面次:面的边界回路长度称为该面的次;
32.一个有限平面图,面的次数之和等于其边数的两倍;
33.欧拉定理:假设一个连通平面图有v个节点,e条边,r个面,则
v-e+r=2;
34.判断是平面图的必要条件:(若不满足,就一定不是平面图)
设图G是v个节点,e条边的简单连通平面图,若v>=3,则e<=3v-6;
35.同胚:对于两个图G1,G2,如果它们是同构的,或者通过反复插入和除去2度节点可以变成同构的图,则称G1,G2是同胚的;
36.判断G是平面图的充要条件:
图G不含同胚于K3.3或K5的子图;
37.二部图:①无向图的节点集合可以划分为两个子集V1,V2;
②图中每条边的一个端点在V1,另一个则在V2中;
完全二部图:二部图中V1的每个节点都与V2的每个节点邻接;
判定无向图G为二部图的充要条件:
图中每条回路经过边的条数均为偶数;
38.树:具有n个顶点n-1条边的无回路连通无向图;
39.节点的层数:从树根到该节点经过的边的条数;
40.树高:层数最大的顶点的层数;
41.二叉树:
①二叉树额基本结构状态有5种;
②二叉树内节点的度数只考虑出度,不考虑入度;
③二叉树内树叶的节点度数为0,而树内树叶节点度数为1;
④二叉树内节点的度数=边的总数(只算出度);握手定理“节点数=边的两倍”是在同时计算入度和出度的时成立;
⑤二叉树内节点的总数=边的总数+1;
⑥位于二叉树第k层上的节点,最多有个(k>=1);
⑦深度为k的二叉树的节点总数最多为-1个,最少k个(k>=1);
⑧如果有个叶子,个2度节点,则=+1;
42.二叉树的节点遍历方法:
先根顺序(DLR);
中根顺序(LDR);
后根顺序(LRD);
43.哈夫曼树:用哈夫曼算法构造的最优二叉树;
44.最优二叉树的构造方法:
①将给定的权值按从小到大排序;
②取两个最小值分支点的左右子树(左小右大),去掉已选的这两个权值,并将这两个最小值加起来作为下一轮排序的权值;
③重复②,直达所有权值构造完毕;
45.哈夫曼编码:在最优二叉树上,按照左0右1的规则,用0和1代替所有边的权值;
每个节点的编码:从根到该节点经过的0和1组成的一排编码;