初识人工智能--决策树算法
机器学习中分类和预测算法的评估:
* 准确率
* 速度
* 强壮行
* 可规模性
* 可解释性
1. 什么是决策树/判定树(decision tree)?
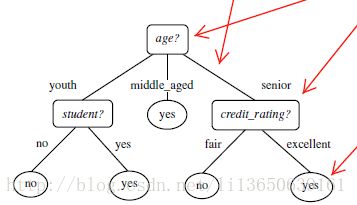
判定树是一个类似于流程图的树结构:其中,每个内部结点表示在一个属性上的测试,每个分支代表一个属性输出,而每个树叶结点代表类或类分布。树的最顶层是根结点。
2. 机器学习中分类方法中的算法
- 朴素贝叶斯(Naive Bayes, NB)
- Logistic回归(Logistic Regression, LR)
- 决策树(Decision Tree, DT) –>本文主要讲述决策树
- 支持向量机(Support Vector Machine, SVM)
3. 构造决策树的基本算法 分支 根结点
结点
树叶
3.1 熵(entropy)概念:
信息和抽象,如何度量?
1948年,香农提出了 ”信息熵(entropy)“的概念
一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常非常不确定的事情,或者是我们一无所知的事情,需要了解大量信息==>信息量的度量就等于不确定性的多少例子:猜世界杯冠军,假如一无所知,猜多少次?
每个队夺冠的几率不是相等的
比特(bit)来衡量信息的多少
![]()
3.1 决策树归纳算法 (ID3)
1970-1980, J.Ross. Quinlan, ID3算法
选择属性判断结点
信息获取量(Information Gain):Gain(A) = Info(D) - Infor_A(D)
通过A来作为节点分类获取了多少信息
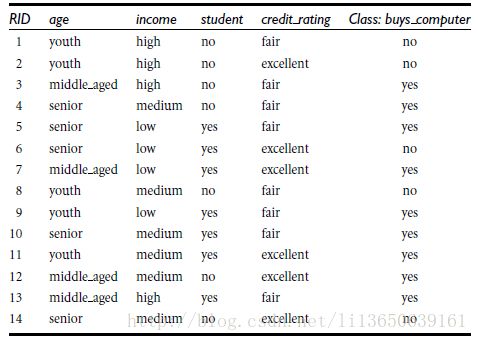
计算过程:先单独计算Info(D),以目标函数为计算基点,总实例数为14,其中no的实例数为5,yes的实例数为9.通过信息熵公式计算,可得:
![]()
再计算包含age属性时的Info_age_(D),其中age可以划分为三个阶段:youth:占实例总数的5/14,middle_aged占4/14,senior占5/14,继续通过信息熵公式计算,得到Info_age_(D),再通过信息获得量公式计算出最后的结果。
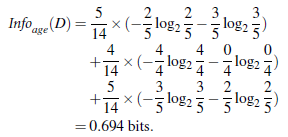
![]()
类似,Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048
所以,选择age作为第一个根节点(取大的)
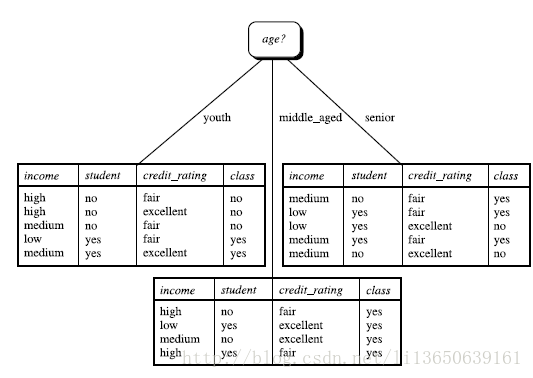
划分好跟节点后,排除已经称为节点的属性,继续通过该方法,可以继续划分结点。若出现划分好的表格中的目标函数为同一类时(eg:yes),便不需要继续划分。
重复以上步骤。。。
算法:
* 树以代表训练样本的单个结点开始(步骤1)。
* 如果样本都在同一个类,则该结点成为树叶,并用该类标号(步骤2 和3)。
* 否则,算法使用称为信息增益的基于熵的度量作为启发信息,选择能够最好地将样本分类的属性(步骤6)。该属性成为该结点的“测试”或“判定”属性(步骤7)。在算法的该版本中,
* 所有的属性都是分类的,即离散值。连续属性必须离散化。
* 对测试属性的每个已知的值,创建一个分枝,并据此划分样本(步骤8-10)。
* 算法使用同样的过程,递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上,就不必该结点的任何后代上考虑它(步骤13)。
* 递归划分步骤仅当下列条件之一成立停止:
* (a) 给定结点的所有样本属于同一类(步骤2 和3)。
* (b) 没有剩余属性可以用来进一步划分样本(步骤4)。在此情况下,使用多数表决(步骤5)。
* 这涉及将给定的结点转换成树叶,并用样本中的多数所在的类标记它。替换地,可以存放结
* 点样本的类分布。
* (c) 分枝
* test_attribute = a i 没有样本(步骤11)。在这种情况下,以 samples 中的多数类
* 创建一个树叶(步骤12)
3.1 其他算法:
C4.5(Quinlan):它能够处理连续型属性或离散型属性的数据;能够处理具有缺失值的属性数据;使用信息增益率而不是信息增益作为决策树的属性选择标准;对生成枝剪枝,降低过拟合。
如下为决策树算法框架:
TreeGrowth(E, F)//E--训练集 F—属性集
if stopping_cond(E, F) = true then //达到停止分裂条件(子集所有样本同为一类或其他)
leaf = createNode() //构建叶子结点
leaf.label = Classify(E) //叶子结点类别标签
return leaf
else"white-space:pre">
root = createNode()"white-space:pre"> //创建结点
root.test_cond = find_best_split(E, F) 确定选择哪个属性作为划分更小子集//
令 V = {v | v是root.test_cond 的一个可能的输出}
for each v V do
Ev = {e | root.test_cond(e) = v and e E}
child = TreeGrowth(Ev, F)
//添加child为root的子节点,并将边(root——>child)标记为v
end for
end if
return root C4.5中用到的几个公式:
<1> 训练集的信息熵
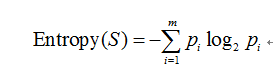
其中 m代表分类数,pi为数据集中每个类别所占样本总数的比例。
<2> 划分信息熵—-假设选择属性A划分数据集S,计算属性A对集合S的划分信息熵值
case 1:A为离散类型,有k个不同取值,根据属性的k个不同取值将S划分为k各子集{s1 s2 …sk},则属性A划分S的划分信息熵为:(其中 |Si| |S| 表示包含的样本个数)

case 2: A为连续型数据,则按属性A的取值递增排序,将每对相邻值的中点看作可能的分裂点,对每个可能的分裂点,计算:
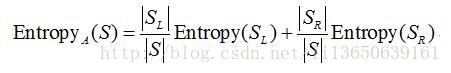
其中,SL和SR分别对应于该分裂点划分的左右两部分子集,选择EntropyA(S)值最小的分裂点作为属性A的最佳分裂点,并以该最佳分裂点按属性A对集合S的划分熵值作为属性A划分S的熵值。
<3> 信息增益
按属性A划分数据集S的信息增益Gain(S,A)为样本集S的熵减去按属性A划分S后的样本子集的熵,即
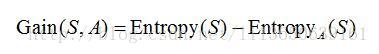
<4> 分裂信息
利用引入属性的分裂信息来调节信息增益
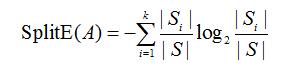
<5> 信息增益率
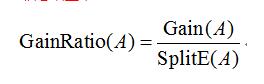
算法:Classification and Regression Trees (CART):
是一种二分递归分割技术把当前样本划分为两个子样本,使得生成的每个非叶子结点都有两个分支,因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树,它在每一步的决策时只能是“是”或者“否”,即使一个feature有多个取值,也是把数据分为两部分。
步骤:
(1)将样本递归划分进行建树过程
(2)用验证数据进行剪枝
参考博文:http://blog.csdn.net/acdreamers/article/details/44664481
以上三种算法共同点:都是贪心算法,自上而下(Top-down approach)
区别:属性选择度量方法不同:
C4.5 (gain ratio), CART(gini index), ID3 (Information Gain)
3.2 如何处理连续性变量的属性?
对于连续性变量的属性,在做决策树算法时,应将其变化为非连续性变量;做法一般是取一个特征值,将其划分为两个或者多个阶段值:eg:年龄–>可以将0-17划分为youth,17-40划分为middle_aged,40-80为senior;这样就可以将连续性的变量划分成非连续性的变量了
4. 树剪枝叶 (避免overfitting):剪枝是决策树停止分支的方法之一
4.1 先剪枝:
在树的生长过程中设定一个指标,当达到该指标时就停止生长,这样做容易产生“视界局限”,就是一旦停止分支,使得节点N成为叶节点,就断绝了其后继节点进行“好”的分支操作的任何可能性。不严格的说这些已停止的分支会误导学习算法,导致产生的树不纯度降差最大的地方过分靠近根节点
4.2 后剪枝:
树首先要充分生长,直到叶节点都有最小的不纯度值为止,因而可以克服“视界局限”。然后对所有相邻的成对叶节点考虑是否消去它们,如果消去能引起令人满意的不纯度增长,那么执行消去,并令它们的公共父节点成为新的叶节点。这种“合并”叶节点的做法和节点分支的过程恰好相反,经过剪枝后叶节点常常会分布在很宽的层次上,树也变得非平衡。后剪枝技术的优点是克服了“视界局限”效应,而且无需保留部分样本用于交叉验证,所以可以充分利用全部训练集的信息。但后剪枝的计算量代价比预剪枝方法大得多,特别是在大样本集中,不过对于小样本的情况,后剪枝方法还是优于预剪枝方法的。
5. 决策树的优点:
直观,便于理解,小规模数据集有效
6. 决策树的缺点:
处理连续变量不好
类别较多时,错误增加的比较快
可规模性一般