点云法向量
一、点云法向量
法向量是点云中各点的重要属性之一。众多点云算法的实施都基于精确的法向量估计,例如许多表面重建算法、点云分割算法、点云去噪算法以及特征描述算法等。
由空间变换可知,点云中每一点的法向量夹角及曲率值均不随物体的运动而改变,具有刚体运动不变性。
点云法向量求解需要其邻域内点支持,而邻域的大小一般由邻域半径值或临近点个数来表示。现实中需要根据点分别率、物体细节精细程度和用途等因素来取值。过大的邻域会抹平三维结构细节使得法向量过于粗糙,而过小的邻域由于包含了太少的点受噪声干扰程度较强。
二、法向量估计方法
1.基于Delaunay三角分割法
基于Delaunay三角分割法不适合有噪声的点云,无法很好的用于现场采集数据集中。
2.基于鲁棒统计学方法
基于鲁棒统计学的方法从原理到计算都过于复杂,因此无法直接用在大规模的点云场景中。
3.基于局部表面拟合法
该方法使用范围最为广泛,且适用于大规模的点云场景中,计算原理较为简单了,效率快。
(1)原理介绍
先对点云中的每个点![]() 以半径A划定邻域范围或者直接选取最近邻的K个点得到邻域内点。此问题转化为使用最小二乘法为邻域内点拟合一个局部平面问题。平面方程的一般表达式为
以半径A划定邻域范围或者直接选取最近邻的K个点得到邻域内点。此问题转化为使用最小二乘法为邻域内点拟合一个局部平面问题。平面方程的一般表达式为![]() ,需要求解的四个参数中,元素不同时为0的向量
,需要求解的四个参数中,元素不同时为0的向量![]() 的实际意义为平面方程的法向量
的实际意义为平面方程的法向量![]() ,而D则为原点到平面的距离。因此,根据最小二乘法推导的局部平面
,而D则为原点到平面的距离。因此,根据最小二乘法推导的局部平面![]() 拟合过程可以表示为:
拟合过程可以表示为:
观察上式,估计点的法向量又可转化为主成分分析问题。平面法向量![]() 需要满足模为1,且
需要满足模为1,且![]() 个邻域内点的质心
个邻域内点的质心![]() 容易求得。
容易求得。
正常情况下,我们可以将质心点![]() 看成是某一领域中所有点的中心点:
看成是某一领域中所有点的中心点:
同时使得![]()
这样,目标函数就可以转化为如下:
再进一步推导可以得到如下关系:
![]()
于是最终可以将优化函数简化为:
![]()
其中满足![]() 、
、![]() 和
和![]() 的条件。
的条件。
对于上述目标函数利用拉格朗日算法进行求解:
假设:![]() 和
和![]()
然后再对变量![]() 求偏导得到如下式子:
求偏导得到如下式子:
![]()
推导出如下结果是根据矩阵转置求偏导的性质和S为协方差矩阵同时为对称矩阵的性质。
为了求得![]() 的最小值,所以必须满足如下关系:
的最小值,所以必须满足如下关系:
![]()
求解![]() 为线性代数里面求解特征值和特征向量的相关公式,即λ是矩阵S的特征值,点云法向量是对应的特征向量。
为线性代数里面求解特征值和特征向量的相关公式,即λ是矩阵S的特征值,点云法向量是对应的特征向量。
(2)求解过程
假设局部平面附近点云数量为m,每个点云表示为![]()
![]() ,所有点云表示记为
,所有点云表示记为![]() 。所以将所有点云变量拼接成一个矩阵,如下:
。所以将所有点云变量拼接成一个矩阵,如下:
根据上面公式推导,计算局部点云的均值,然后在原来点云矩阵上减掉对应方向上的均值![]() ,重新构造新的点云变量矩阵,如下所示:
,重新构造新的点云变量矩阵,如下所示:
在统计学中,协方差用来刻画两个随机变量之间的相关性,反映的是变量之间的二阶统计特性,考虑两个随机变量![]() 和
和![]() 他们的协方差矩阵定义为
他们的协方差矩阵定义为
![]()
协方差为零表示两个变量之间线性不相关。![]() 维随机变量
维随机变量![]() 的协方差矩阵定义为
的协方差矩阵定义为
其中![]() 。显然,矩阵C是一个对称矩阵。协方差矩阵C中的对角线元素表示方差,非对角线元素表示随机X的不同分量之间的协方差。若不同分量之间的相关性越小,则C的非对角线元素的值就越小。
。显然,矩阵C是一个对称矩阵。协方差矩阵C中的对角线元素表示方差,非对角线元素表示随机X的不同分量之间的协方差。若不同分量之间的相关性越小,则C的非对角线元素的值就越小。
经过复杂公式推导,对于拟合成局部平面的点云集之间各变量相关性的协方差矩阵存在如下关系:
需要注意是:协方差矩阵C是否除点云集数量m,对求解特征向量没有影响。所以基于构建点云集的协方差矩阵与第一部分原理介绍矩阵有着特征向量,就这样我们就能求出基于局部平面拟合点云的法向量。
根据上文原理介绍,求解所有点云到拟合局部平面的最短距离可以简化为求解协方差矩阵的最小特征值,即满足![]() 的最小特征向量,S的值为
的最小特征向量,S的值为![]() ,该矩阵为一个3×3的实对称矩阵(非方阵没有特征值和特征向量)。
,该矩阵为一个3×3的实对称矩阵(非方阵没有特征值和特征向量)。
特征值和特征向量求解: ![]()
![]()
特征方程:
使得特征方程为零,求得多个特征值,并将特征值带入到![]() ,求解出对应是特征向量。选择最小特征值对应的特征向量,并进行单位化,则该向量为点云法向量。
,求解出对应是特征向量。选择最小特征值对应的特征向量,并进行单位化,则该向量为点云法向量。
上述求解点云法向量的形式与PCA降维求解协方差矩阵的特征值和特征向量相同,于是我们可以借用PCA原理进行求解点云的法向量。需要注意是:基于PCA降维求解协方差矩阵的特征值要求越大越好,其特征向量就越能描述数据的特征,小就越不能区分样本之间的不同,也就是表征了数据中的共性。在我们的优化目标函数中,就是要为所有的邻域点寻找一个平面,使得所有的邻域点都在这个平面上,或者说所有点与该平面的距离最小,所以要求我们选择协方差矩阵的最小特征值和对应特征向量。
在求出法向量后还需要判断法向量的方向,一般来说法向量方向的矫正没有严格的数学公式可以使用。比较简单的方法是通过视点方向进行判断。比如我的视点方向是(0,0,1),那么求出来的法向量跟(0,0,1)进行点乘,如果小于0,就将法向量取反。更复杂的方法是使用最小生成树对法向量进行方向矫正。
参考文献
1.点云法向量估计:https://blog.csdn.net/linmingan/article/details/80586214
2.协方差矩阵推导:https://blog.csdn.net/itplus/article/details/11452743
3.PCA估计点云法向量:https://zhuanlan.zhihu.com/p/56541912
4.PCA原理介绍:https://zhuanlan.zhihu.com/p/37777074
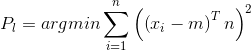


![P_{l}=min\sum_{i=1}^{n}\left ( \left y_{i}\right^{T} n \right )^{2}=min\sum_{i=1}^{n}n^{T}y_{i}y_{i}^{T}n=min\left [n^{T} \left ( \sum_{i=1}^{n}y_{i}y_{i}^{T} \right )n\right ]](http://img.e-com-net.com/image/info8/ba78e19e8f0c4304994572a1e90d6c2d.gif)