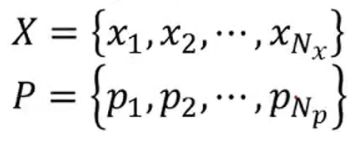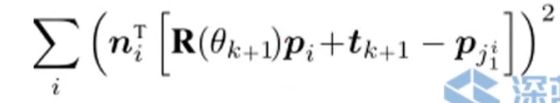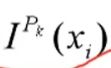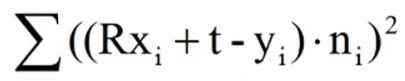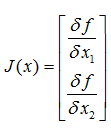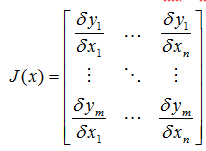激光SLAM——第四节（激光SLAM的前端配准方法）
@[目录]
ICP变种方法
– 第四章 激光的前端配准算法（ICP）
4.1、2、3、4的ICP方法，一个比一个精度高，计算量也大。
点云匹配算法是为了匹配两帧点云数据，从而得到传感器（激光雷达或摄像头）前后的位姿差，即****里程数据。匹配算法已经从最初的ICP方法发展出了多种改进的算法NDT。他们分别从配准点的寻找，误差方程等等方面进行了优化。下面分别介绍：
4.1 ICP匹配方法
点对点的icp，可以称PP-icp
- Iterative closest point：迭代最近点（最原始的icp算法）
- 简介：前端匹配（配准），后端优化；套路是固定的，即求解最小二乘解。基于图优化的slam如果做得精度高，那多半是前端配准做得棒，才可以拉开差距。
- 目地：配准两帧点云，求欧式变换（R、t变换）；
- 意义：两个安装方法、角度不同的雷达，对同一个实体看到的样子是不一样的（距离、姿态等），设为两个雷达探知到的同一个实体位姿为A、B，求A、B位姿的变换，（R、t变换、欧式变换问题）
- 两帧点云集合X、P：
– 4.1.1 已知对应解的求解方法–证明
- 一般是没办法不迭代就知道对应解的；
勘误：假设矩阵A为正定对称矩阵
– 4.1.2 未知对应点的求解方法
笔记的3.2.4同此；
迭代最近点求解流程（ICP通用方法）：
- 1、寻找对应点（需要初始输入的R、t），由R、t求‘对应点’；
- 2、根据对应点，再求解进一步的R、t，由‘对应点’求解R、t；
- 3、对点云进行转换，计算误差；
- 4、不断重复123点，迭代求解，直到误差小于某阈值；
将匹配的方法求解成EM算法思想；
4.2 PL-ICP匹配方法
后面的ICP的优化方法，都是基于这个优化思想。
- PL：point to line
- 示意图：
- a黄色表示实际曲线，蓝色表示激光采样的点；黑色表示和黄色近似的‘曲面’。
- b是点对点，势场是圆，往四周扩展递增，和实际不符合；
- c是点对线的势场模型，势场都是平行的，往外递增，比较符合实际。
– 4.2.1基本思想：
- 1、激光点是对实际环境的曲面的离散采样；
- 2、重要的不是激光点，而是隐藏在激光点中的曲面；
- 3、最好的误差尺度为当前的激光点到实际曲面的距离，关键的问题在于如何恢复曲面；
- 4、PL-ICP的解答思路：用分段线性的方法来对实际曲面进行近似，从而定义当前帧激光点到曲面的距离；
– 4.2.2 数学描述：
- 目标函数：表示点到曲面的距离，即点到直线的距离
– 4.2.3 求解方法：
- 流程：
1、把当前帧的数据根据初始位姿投影到参考帧坐标系下；
2、对于当前帧的点i，在参考帧中找到最近的两个点（j1，j2）****，因为两点确定一线。
3、计算直线误差，并去除误差过大的点。
4、代入最小化误差函数求解，点到直线的误差。
– 4.2.4 PL-ICP和ICP的区别
4.3 NICP匹配方法
- **N：normal **法向量
简介：原始的论文是运行在3D激光中的，不过变到2D是很容易的。
目前在开源领域最好的ICP方法；
– 4.3.1 基本思路：
1、替换了pp-icp的欧式最近距离特征。
2、充分利用曲面的特征来对错误的点匹配进行滤除，主要的特征为法向量和曲率。
3、误差项除了考虑对应点的欧式距离之外，同时还考虑对应点法向量的角度差。（有利于R旋转矩阵的求解，精度更高**；R比t的精度要求高**）
– 4.3.2 数学描述
– 4.3.3 法向量和曲率计算
高斯分布，描述点云的空间分布特性，即usi；
– 4.3.4 点匹配规则：
1、杂点不匹配
J的求解，泰勒展开；LM迭代求解收敛。
– 4.3.5 算法流程：
4.4 IMLS-ICP匹配方法
- IMLS：隐式的移动最小二乘；
- Implicit 隐式，由于实际的曲面的显式方程难以求出，实际是求点到曲线的距离，拟合一曲面。
- Moving 滑动窗口法：
- Least Square 最小二乘法求解；
理论上最好的算法，因为对实际环境的拟合是最真实的，精度最高。
目前没有开源的slam的ros算法包；
曲面重建约准确，对真实世界描述约准确，匹配的精度就越高。
步骤：
1、选取参考点；
2、曲面重构；
– 4.4.1 ICP和IMLS的对比：
1、ICP收敛到了一团点上，收敛结果不稳定；
2、IMLS-ICP收敛到了曲线上，符合真实情况，拟合结果稳定，误差尺度更好；
基本思想解释：
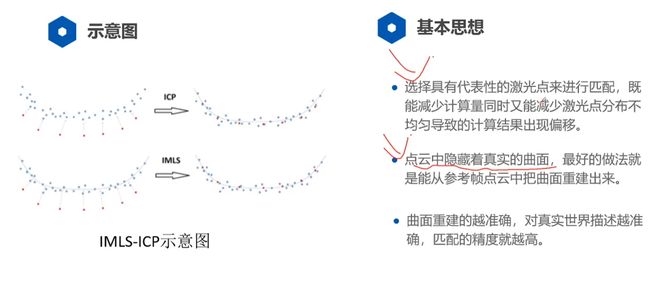
1、选择代表性点：选择信息量丰富的点，结构化的点。去除不好的杂点，因为激光常常会出现点分布不均匀的情况，可能会让最终匹配结果偏向特征点丰富的一边，令匹配失真；
– 4.4.2 代表点的选择策略：
- 2D激光：选择直线；
- 3D激光：选择平面；
解释：
1、选择结构化的点，具有良好的曲率和法向量，选择均衡，在曲面两侧数量基本平衡
2、角度不可观一般遇不到，除非是一个非常圆的环境，没有别的特征，难以分辨方位。
– 4.4.3 曲面重建方法
– 4.4.4 匹配求解
- 计算步骤：
- 当前帧中的一点xi到曲面的距离
； - Pk中离点xi最近的点的法向量为ni；
- 则点xi在曲面上的投影yi为：yi=xi-Ipk(xi)*ni
- 点xi和点yi为对应的匹配点：
- 当前帧中的一点xi到曲面的距离
基于优化的方法
– 第五章 激光前端配准算法（基于优化/势场方法）
以下为基于势场的方法，与ICP算法不一样，以下算法都不需要匹配点；简单来说就是对某段连续的激光点（障碍物）进行高斯平滑/膨胀，再用分数评价，离激光点（障碍物）越近，得分越高（障碍物本身得分为零），人为地构造出一个得分势场； 这样只要比较得分即可，不需要匹配点。
- 基本数学概念：
a.梯度gradient，由多元函数的各个偏导数组成的向量
以二元函数为例，其梯度为：
b.黑森矩阵Hessian matrix，由多元函数的二阶偏导数组成的方阵，描述函数的局部曲率，以二元函数为例。可用迭代法求解，地址
c.雅可比矩阵 Jacobian matrix，是多元函数一阶偏导数以一定方式排列成的矩阵，体现了一个可微方程与给出点的最优线性逼近。以二元函数为例，
如果扩展多维的话F: Rn-> Rm，则雅可比矩阵是一个m行n列的矩阵：
雅可比矩阵作用：如果P是Rn中的一点，F在P点可微分，那么在这一点的导数由JF§给出，在此情况下，由F§描述的线性算子即接近点P的F的最优线性逼近：
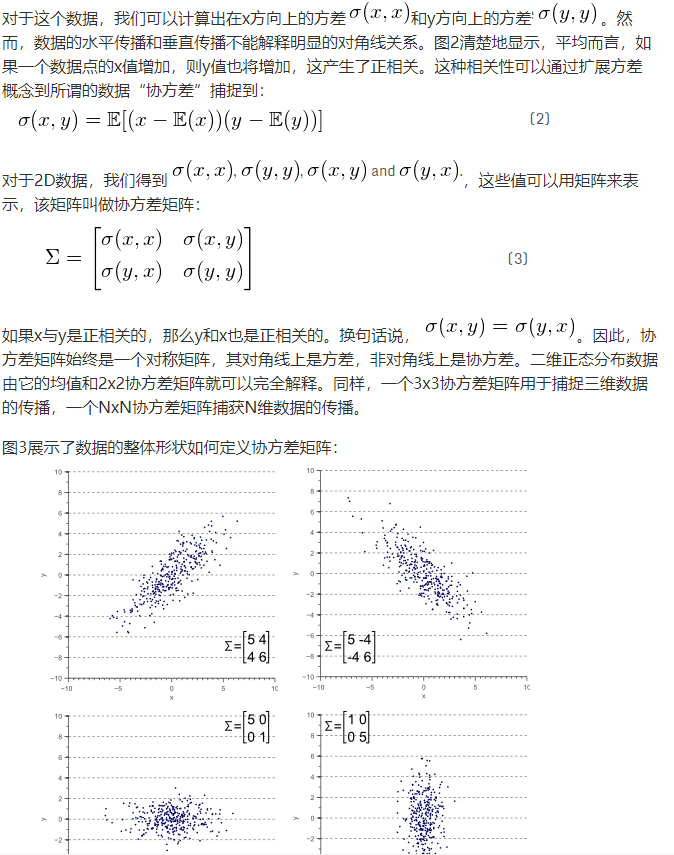
d.残差 residual，表示实际观测值与估计值(拟合值)之间的差值
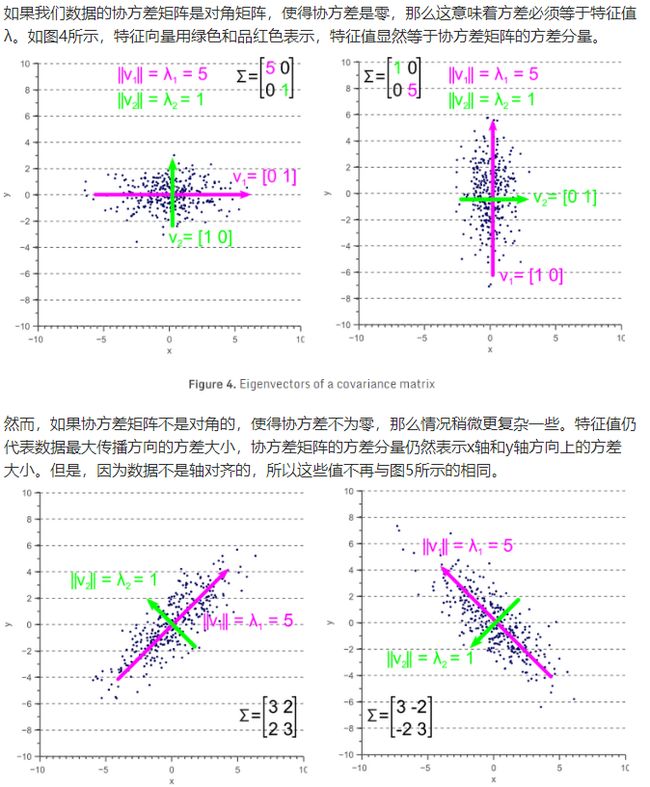
e. 协方差矩阵
资料：
http://www.360doc.com/content/16/0121/13/13800296_529534763.shtml
协方差矩阵始终是一个对称矩阵，其对角线是方差，非对角线是协方差；
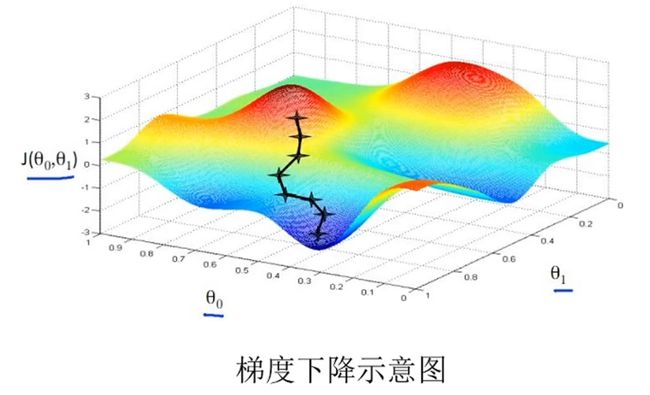
5.1高斯牛顿优化方法
例如：hector-slam。
算法解析：https://blog.csdn.net/qq_39521554/article/details/79919041
** 高斯牛顿法解决非线性最小二乘问题的最基本方法，并且它只能处理****二次函数**
– 5.1.1 原理图示及数学描述
描述：此图表示红色最高点为选取的初始值，取不同的初始解，会得到不一样的结果。（非凸优化、初始值敏感）。下图就是人工势场。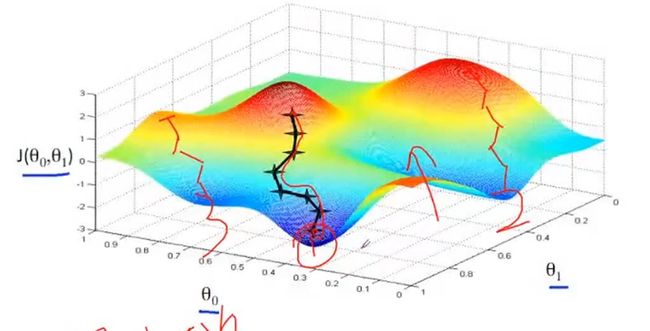
给定目标函数E(T):
- 上图公式：
1、目标是求T（机器人位姿）的极小值；
2、[1-M(Si(T))]²，表示势场（其中Si表示得分，M(x)表示得到坐标X的地图占用概率），即表示在障碍物周围一定区域内，得分表示为1，超过区域表示为0，这就有了一个人工势场（ [0, 1]闭区间 ）。
3、生成T的坐标矩阵，将T全部转换到三维空间中。
– 5.1.2 求解方法步骤
- pi表示当前激光帧的第i个激光点参考坐标/势场坐标；
- M(Si(T))为非线性函数；一阶泰勒展开得线性函数，化简
- M(Si(T))是离散的，无法求导，故需要插值。
- 地图的插值方法：
1、地图双线性插值
如上图，Pm为激光点，已知Pij四点栅格值，且知道其各自的势场值，就可用双线性插值方法推出Pm的势场值；
- 拉格朗日插值法
一般来说多项式插值就是求n-1个线性方程的解，拉格朗日插值即是基于此思想。拉格朗日创造性的避开的方程组求解的复杂性，引入“基函数”这一概念，使得快速手工求解成为可能。
定义：求作<=n 次多项式 pn（x），使满足条件pn（xi）= yi，i = 0，1，…，n.这就是所谓拉格朗日（ Lagrange）插值；
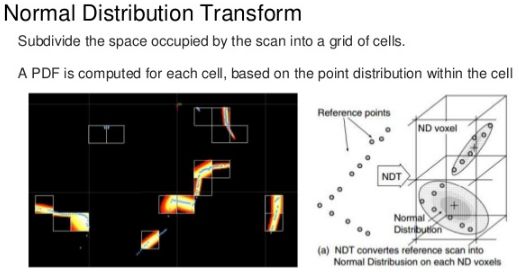
5.2 NDT方法
主要用在3D-slam算法当中。
- 比较好的NDT解析：https://www.cnblogs.com/21207-iHome/p/8039741.html
– 5.2.1 基本思想
NDT算法的基本思想是先根据参考数据（reference scan）来构建多维变量的正态分布，如果变换参数能使得两幅激光数据匹配的很好，那么变换点在参考系中的概率密度将会很大。因此，可以考虑用优化的方法求出使得概率密度之和最大的变换参数，此时两幅激光点云数据将匹配的最好。
Normal Distance Transform 正态分布变换；
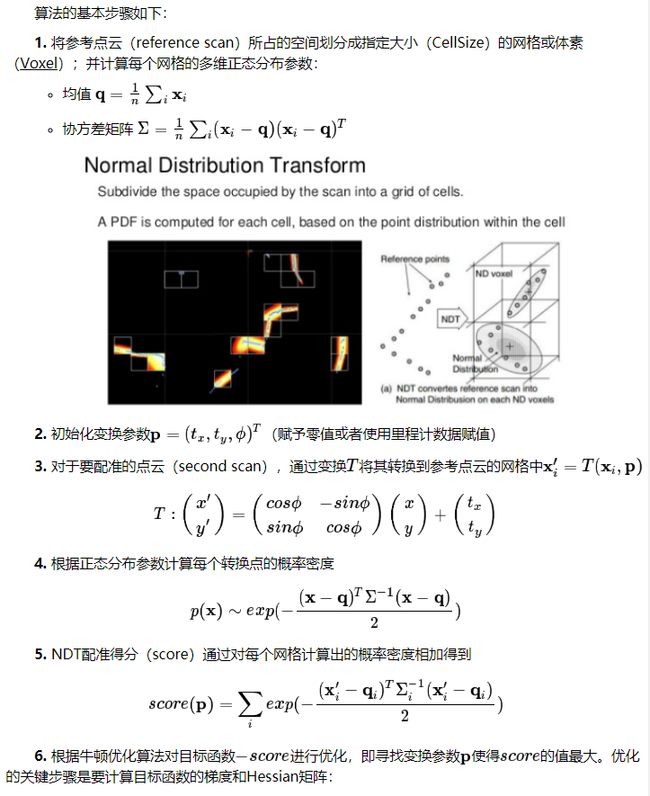
1、把空间用cel进行区分
2、用高斯分布区代替势场，膨胀为符合正态分布的概率密度区域，形成一个天然分段连续的势场：
把落入cell的点都认为符合拟合的高斯分布。
– 5.2.2 数学描述
– 5.2.3 算法流程
NDT算法的C++实现：
https://blog.csdn.net/adamshan/article/details/79230612
5.3 相关匹配方法及分支定界加速
CSM、BB
例如：cartographer。
CSM作用：先用相关性扫描匹配（CSM）给一个初值，然后构造一个最小二乘问题；用激光末端点匹配取到占据栅格地图中的值，获得得分，取得分最高的作为初值。加上多分辨率计算可以加速，并且获得分辨率意义下的最优解。
相关性扫描匹配的思路其实非常简单。想象给定一个栅格地图，再给定当前帧的点云，怎样才能知道激光雷达所在的位置呢？最简单的办法，**把激光雷达放在地图的每个格子上，看在这个位置时，**点云是否与地图重合，重合程度最高的位置就是激光雷达的真实位姿。
- 基本概念
枚举似然场中的每一个位姿，选择最好的。
– 5.3.1 算法流程
1、构造似然场，即对其进行高斯模糊；
2、指定一个小车的位姿范围，例如1m x 1m，30度范围内，分成许多位姿，计算每一个位姿的得分，取最优解。
3、位姿搜索
- 位姿搜索
1、暴力搜索
三层嵌套for循环，大量三角函数计算。
2、预先投影搜索
把1的顺序调转。
3、多分辨率搜索
因为25cm和2.5cm的差距，保证不了最优位姿在栅格内，所以有时候会得到一个次优解。分支定界可能最优。
5.4 分支定界算法
– 5.4.1 基本思想
– 5.4.2 分支定界的加速作用
补充
相关性扫描匹配CSM与分支限界加速：
https://blog.csdn.net/weixin_35695879/article/details/103511418
Google Cartographer SLAM 原理 （Real-Time Loop Closure in 2D LIDAR SLAM 论文详细解读）：
https://blog.csdn.net/weixin_36976685/article/details/84994701
前言
在激光SLAM中，相关性扫描匹配可是重点中的重点，而分支限界加速更是大大提高了它的实时性。本文就来详细解读一下其中的奥秘。
激光SLAM前端
既然是SLAM，那么通常都会分为前端和后端。前端充当里程计的角色，比如我们熟知的VO（视觉里程计）和VIO（视觉惯性里程计）。激光SLAM也需要前端，对于每一帧点云，通常是使用所谓的扫描匹配（scan-match）方法进行位姿估计。
简单地说，扫描匹配就是想办法把两帧点云对齐，对齐过程中的旋转和平移就是两帧之间的相对位姿。这是最最简单的方式，实际中，为了提高鲁棒性，通常把当前帧点云和地图进行扫描匹配，更不容易出错。
扫描匹配的实现方式有两种，第一种是相关性扫描匹配，第二种是基于优化的扫描匹配。第一种思路简单，但有一些复杂的细节，而第二种则是构建非线性最小二乘优化问题并求解。实际中，通常是两种方法同时用，先用相关性扫描匹配求初值，再用基于优化的扫描匹配进一步优化。
相关性扫描匹配
相关性扫描匹配的思路其实非常简单。想象给定一个栅格地图，再给定当前帧的点云，怎样才能知道激光雷达所在的位置呢？最简单的办法，把激光雷达放在地图的每个格子上，看在这个位置时，点云是否与地图重合，重合程度最高的位置就是激光雷达的真实位姿。
显然，这个方法就是暴力搜索。虽然肯定搜得出来，但速度比较慢。想要加速，就得祭出我们的算法神器了——分支限界。
分支限界加速
如果上过计算机算法课，就一定接触过分支限界法。这是一个通用的算法，一般用于搜索离散空间的最优解。我们这里的解空间显然就是一个离散的空间，而且可以很方便地按照地图分辨率构造树形结构。
举例来说，假设有一张4×4的地图，我们降低其分辨率，每2×2的格子合并成一个，得到一张2×2的地图，再降低其分辨率，得到一张1×1的地图。这样，地图被分成了三层，如下图所示。
有了多分辨率地图后，我们先在第二层的解空间中搜索，找到最优的位姿对应的格子。然后再在该格子中搜索下一层中对应的小格子，找到最优的位姿。
这么简单？当然不是。请注意，上面的做法是完全错误的。它有两个问题。首先，在第二层的格子中搜索最优的位姿，实际上是把位姿放在格子的中心，计算其点云的评分（即hit点的评分之和，下文直接称其为位姿的评分）。但是格子中心的位姿并不能代表格子其它位置的位姿，很有可能格子中心的评分低于其它位置的评分，那么第二层最优的格子中并不一定包含第三层最优的格子。怎么办呢，我们可以想办法让格子中心的评分高于其所有子格子的评分，此时格子的评分是其子格子的评分上界，这样就可以保证子格子的最高评分体现在父格子中。
但是，此时又引入了第二个问题，虽然格子的评分是其子格子的评分上界，但并非上确界。也就是说，可能存在格子的评分很高，但其所有子格子的评分都很低的情况。这样的话，我们仍然无法选取最大评分格子的同时抛弃其它格子。
剩下的选择就只有一个，绝不抛弃任何一个可能存在最优解的格子，只抛弃那些绝对不存在最优解的格子。这正是分支限界的思想。
具体实现的时候，先从根节点开始遍历，把它拆分成4个子格子。这4个子格子分别计算评分，并由高到低排序。从中选出分数最高的格子，进一步拆分成4个子格子。假设这4个子格子已经到了叶子节点，也就是达到了真实地图的分辨率。此时计算出的4个子格子的评分代表了真实的位姿评分（只有叶子节点的评分是真实评分，其它格子的评分都是上界），找出其最大值，记作best_score。以上过程，我们体会了分支是如何实现的。接下来，该轮到限界出场了。第二层的格子还有3个未曾探索，我们当然是选择最大的那个开始分支。但别急，先看一下它的评分是否大于best_score，如果是，继续分支，如果否，就可以直接剪枝了，抛弃这个格子及其所有子格子。因为格子的评分代表了其子格子评分的上界，如果上界都小于best_score，就不可能再有子格子的评分大于它了。按照如此方法，大刀阔斧地剪枝即可。注意，当遇到评分大于best_score的叶子节点时，记得更新best_score，这样可以更快地缩小搜索空间。
讲到这里，你是不是有点摸不着头脑？别怕，因为这里有个最最关键的问题我还没有解释，也就是如何能够快速计算出格子评分的上界。
计算评分上界
先说一个平凡方法。既然要算子格子评分的上界，那就把每一个子格子拿出来算一遍，求个最大值。对了，子格子还会有子格子，所以这是个递归运算，直到把叶子节点都算出来才行。那这跟直接暴力搜索就没什么两样了，不行不行。
我们还是得追求在O(1)时间复杂度内求出格子的评分。想了想，之所以叶子节点评分可以在O(1)时间内求出，是因为它是直接在地图中查表得到的（严谨地说，是通过查其所有hit点的评分再求和得到的，但由于hit点数量固定，可以认为时间复杂度是O(1)）。但我们构造的多分辨率地图能不能也维护类似的概率表格，使得格子的评分可以在对应分辨率地图中查询得到呢？
多么机智的想法啊！试想，把地图中每个格子的概率用其附近区域内的最大概率代替。这样的话，直接查对应分辨率地图就可以得到格子的评分，因为这个评分已经事先在附近区域中取了最大值。
上面提到的“某个范围”，需要与地图分辨率保持一致。也就是说，越低分辨率的地图（也就是越高层的地图），应该在越大的区域求最大值，其大小与当前分辨率下格子的大小一致。
不同分辨率的地图需要事先计算好，大概长这个样子：
可以看到，越靠后的地图分辨率越低，格子中的概率越接近1，也就代表了越高的上限。这与我们的直观理解是一致的。
总结
说实话，本文内容非常抽象，又限于笔者画图能力太差，实在画不出合适的插图，只能靠读者自己想象了。
不得不说，除非事先有所了解，否则读了之后可能还是一头雾水。所以，如果你对激光SLAM还没有整体的了解，还不知道什么是点云、什么是地图、如何计算概率。那么请关注一下文末的参考资料，相信会对你有所帮助。
相关性扫描匹配及分枝限界加速在谷歌Cartographer的论文中有详细介绍，建议大家去看一看。
参考资料
Real-Time Loop Closure in 2D LIDAR SLAM Wolfgang Hess, Damon Kohler, Holger Rapp, Daniel Andor