一个0-1规划的建模例子
记录一个关于0-1规划问题(指派问题、分配问题)模型的建立、实现、求解的过程,并在基础模型通过添加惩罚或激励机制考虑多种情况。记录目的在于学习交流以及日后自己对该类模型能进行较快的进行描述实现。
问题描述(基础)
考虑这么一个分配问题有9个数,让他们其中分成2组每组不超过6人,每组又分成A、B两队,每队不超过3人。目标使得每组A、B两队和之差最小。用数学题的语言进行描述该问题,现有9人,分成2组,每组最多6人,每组内又分AB两队,如何安排才能使得每组两队分数较为平衡。
思考解的形式
我们将解分成2*2个(两组每组两队)部分,每个部分需要重9个数中进行选择,用0-1来表示在该部分中是否被选中,那么它的解的个分别数为9*2*2,用矩阵形式为:

将其用向量的形式进行表示:

思考约束条件以及目标
解的形式确定之后,思考如何针对该解的形式,然后对问题进行描述,从问题中和解的形式,我们可以总结出以下的2个约束:
- 每组中的A部分和B部分分别小于等于3人
- 每个数只能出现1次,即每一列的和为1
用公式进行表达为:
∑j=113x1ja<=3∑i=13xi1a<=1∑j=113x1jb<=3∑i=13xi1b<=1......
思考目标两队分数之和比较接近,可以理解每一组中为:
其中x表示9个数的位置(0-1表示),y表示对应位置的数的值,即使得每组A队的分数尽可能大并且接近该组之和的1/2。将其组合起来可以该总目标表示为:
最后将问题进行重新进行整理
- 目标为:A队之和最大
- 约束1: 每队小于等于3人
- 约束2: 每组A队小于B队
- 约束3: 每个数只能出现1次,即每一列和为1
代码实现
主代码,函数在附录。
## 注: 函数查看附录
arfa <- 10 # 目标扩大比例。多目标考虑时用于调节目标权重
################## par1 生成随机数 ###
size <- 9
ySimu <- sample(200:8000, size = size)
# [1] 657 1540 566 2997 621 5916 4955 3944 5299
yNum <- rep(1, size)
# 解的基础列数,基础行数
nCol <- sum(yNum)
nRow <- 3
################## par2 目标描述 ###
# A队总分占总分接近一半,除以1/2sum(ySimu)用于将目标化再0-1之间。
obj1 <- c(rep(ySimu, nRow), rep(0, nRow*nCol))/(1/2*sum(ySimu)) * arfa
Cobj <- NULL
################## par3约束条件生成 ###
matMatrixA1 <- matA1(nRow, nCol, Cobj) # 行约束1:行约束, 行之和 <= 5, 约束X_ija
matMatrixA2 <- matA2(nRow, nCol, Cobj, y=ySimu) # 行约束2: A队分数小于B队
matMatrixA3 <- matA3(nRow, nCol, Cobj) # 列约束1:X_ija + X_ijb == 1
################### part4 求解 ###
# 约束整理
obj <- obj1
condition <- SummaryCondition(list(matMatrixA1, matMatrixA2,
matMatrixA3)) # 条件约束
# 方程求解
solve <- Rsymphony_solve_LP(obj,
condition$mat,
condition$dir,
condition$rhs,
max = TRUE, types = "B")
################### part5 结果查看 ###
ResultCheck(solve, obj1, matMatrixA2$mat)
# 结果行检查: 5 4
# 结果列检查: 1 1 1 1 1 1 1 1 1
#----------------------------#
# 约束条件2检查: -70 -77
#----------------------------#
# 分队结果 1 : 2997 4955 -1540 -566 -5916
# 分队结果 2 : 657 621 3944 -5299
#----------------------------#
# optimum: 9.944518
# obj1 A队接近B队 : 9.944518 添加其他条件
通常情况下,现实问题中存在更多情况需要进行考虑。例如在上述问题中,除了希望使得AB两队之和相差不大之外,我们更希望它的分配中每组尽量筹够6个数,然后再进行考虑下一组分配。因此,新建一个变量,用0-1表示该组是否满6个数,假如是,那么该项应对目标有促进用。用公式表达为:
那么其解变为:
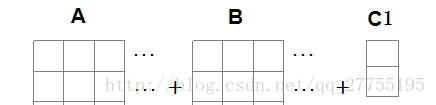
向量形式为:

其需添加约束为:
代码实现
gamma <- 10
################## par2 目标描述 ###
# 用于评判是否满6人,除以(1/nRow)用于将目标化再0-1之间。
obj2 <- rep(1, nRow)*(1/nRow) * gamma
Cobj <- list(obj2)
################## par3 约束条件生成 ###
matMatrixC1 <- matC1(nRow, nCol, Cobj) # 惩罚约束1:尽可能的满簇
################### part4 求解 ###
# 约束整理
condition <- SummaryCondition(list(matMatrixA1, matMatrixA2,
matMatrixA3, matMatrixC1)) # 条件约束
# 方程求解
obj <- c(obj1, obj2)
solve <- Rsymphony_solve_LP(obj,
condition$mat,
condition$dir,
condition$rhs,
max = TRUE, types = "B")
################################### 结果检验
ResultCheck(solve, obj1, obj2, matMatrixA2$mat)
# 结果行检查: 3 6
# 结果列检查: 1 1 1 1 1 1 1 1 1
#----------------------------#
# 约束条件2检查: -340 -11
#----------------------------#
# 分队结果 1 : 621 4955 -5916
# 分队结果 2 : 657 1540 5299 -566 -2997 -3944
#----------------------------#
# optimum: 14.86752
# obj1 A队接近B队 : 9.867522
# obj2 尽可能满簇 : 5 总结
最近开始研究分配问题以及指派问题,并尝试将其运用到实际项目当中,记录该文章,以便以后遇到类似的问题,能够快速按照此思路进行分析建立问题,以缩短建模、实现时间。
上述的问题的求解过程,我思考的过程是,先进行思考基础解的形式,然后在解的形式确定下,需要添加什么条件才能满足题目基础要求,最后在满足基础要求下,开始思考添加其他更多考虑元素。在目标上,尽量将其标准化到0-1之间有利于调节不同考虑因素的平衡。
关于问题上,其实还可以继续的添加条件,例如,当这几个数中有捆绑的时候,应该如何添加约束条件,当我希望组内最大最小值范围变小的时候应该如何添加条件。
附录
几个函数。分别为约束1、2、3和约束C1。
##################### 约束函数 ###########################
matA1 <- function(nRow, nCol, Cobj){
# 行约束1:行约束, 行之和 <= 5, 约束X_ija
# Args: nRow:预分配行数
# nCol:变量个数
# Cobj:惩罚目标
# return: 约束1的mat, dir, rhs。list格式存储
# 行约束, 行之和 <= 5, 约束X_ija
matMatrixA1a <- matrix(0, nrow = nRow, ncol = nRow*nCol)
for(i in 1:nRow){
rst <- matrix(0, nrow = nCol, ncol = nRow)
rst[,i] <- 1
rst <- as.numeric(rst)
matMatrixA1a[i, ] <- rst
}
# 行约束, 行之和 <= 5, 约束X_ijb
matMatrixA1b <- matMatrixA1a
## 约束1整理
matMatrixA1a <- cbind(matMatrixA1a, matrix(0, nrow = nRow, ncol = nRow*nCol)) # B的位置预留
matMatrixA1b <- cbind(matrix(0, nrow = nRow, ncol = nRow*nCol), matMatrixA1b) # A的位置预留
matMatrix <- rbind(matMatrixA1a, matMatrixA1b)
## 惩罚位置生成
for(i in 1:length(Cobj)){
matMatrix <- cbind(matMatrix, matrix(0, nrow = nrow(matMatrix), ncol = length(Cobj[[i]]))) # 惩罚
}
## 左右约束
dirA1 <- rep("<=", nRow*2)
rhsA1 <- rep(3, nRow*2)
# 结果整理
csq <- list(matMatrix, dirA1, rhsA1)
names(csq) <- c("mat", "dir", "rhs")
csq
}
matA2 <- function(nRow, nCol, Cobj, y){
# 行约束2: A队分数小于B队
# Args: nRow:预分配行数
# nCol:变量个数
# Cobj:惩罚目标
# y :值
# return: 约束2的mat, dir, rhs。list格式存储
matMatrixA1a <- matrix(0, nrow = nRow, ncol = nCol*nRow)
matMatrixA1b <- matrix(0, nrow = nRow, ncol = nCol*nRow)
for(i in 1:nRow){
rst <- matrix(0, nrow = nCol, ncol = nRow)
rst[, i] <- 1
rst <- as.numeric(rst)
matMatrixA1a[i,] <- rst
matMatrixA1b[i,] <- rst * -1
}
matMatrixA1a <- matMatrixA1a * matrix(rep(y, nRow*nRow), nrow = nRow, byrow = T)
matMatrixA1b <- matMatrixA1b * matrix(rep(y, nRow*nRow), nrow = nRow, byrow = T)
# 结果整理
matMatrix <- cbind(matMatrixA1a, matMatrixA1b)
# 惩罚项添加
for(i in 1:length(Cobj)){
matMatrix <- cbind(matMatrix, matrix(0, nrow = nrow(matMatrix), ncol = length(Cobj[[i]]))) # 惩罚
}
dir <- rep("<=", nRow)
rhs <- rep(0, nRow)
# 结果整理
csq <- list(matMatrix, dir, rhs)
names(csq) <- c("mat", "dir", "rhs")
csq
}
matA3 <- function(nRow, nCol, Cobj){
# 列约束1:X_ija + X_ijb == 1
# Args: nRow:预分配行数
# nCol:变量个数
# Cobj:惩罚目标
# return: 约束2的mat, dir, rhs。list格式存储
matMatrixA1a <- matrix(0, nrow = nCol, ncol = nCol*nRow)
matMatrixA1b <- matrix(0, nrow = nCol, ncol = nCol*nRow)
for(i in 1:nCol){
rst <- matrix(0, nrow = nCol, ncol = nRow)
rst[i, ] <- 1
rst <- as.numeric(rst)
matMatrixA1a[i, ] <- rst
matMatrixA1b[i, ] <- rst
}
matMatrix <- cbind(matMatrixA1a, matMatrixA1b)
# 惩罚项添加
for(i in 1:length(Cobj)){
matMatrix <- cbind(matMatrix, matrix(0, nrow = nrow(matMatrix), ncol = length(Cobj[[i]]))) # 惩罚
}
dir <- rep("==", nCol)
rhs <- rep(1, nCol)
# 结果整理
csq <- list(matMatrix, dir, rhs)
names(csq) <- c("mat", "dir", "rhs")
csq
}
matC1 <- function(nRow, nCol, Cobj, Cidx = 1){
# 惩罚约束1:尽可能的满簇
# Args: nRow:预分配行数
# nCol:变量个数
# Cidx:惩罚项位置
# return: 惩罚项约束的mat, dir, rhs。list格式存储
matMatrixC1a <- matrix(0, nrow = nRow, ncol = nCol*nRow)
matMatrixC1b <- matrix(0, nrow = nRow, ncol = nCol*nRow)
for(i in 1:nRow){
rst <- matrix(0, nrow = nCol, ncol = nRow)
rst[, i] <- 1
rst <- as.numeric(rst)
matMatrixC1a[i, ] <- rst
matMatrixC1b[i, ] <- rst
}
matMatrixC1 <- cbind(matMatrixC1a, matMatrixC1b)
matMatrixC1corr <- matrix(0, nrow = nrow(matMatrixC1), ncol=nRow)
for(i in 1:nRow){
matMatrixC1corr[i, i] <- -3*2
}
for(i in 1:length(Cobj)){
if(i < Cidx){
matMatrixC1 <- cbind(matMatrixC1, matrix(0, nrow = nrow(matMatrixC1), ncol = length(Cobj[[i]]))) # 惩罚1:尽可能满簇
}else{
if( i == Cidx){
matMatrixC1 <- cbind(matMatrixC1, matMatrixC1corr)
}else{
matMatrixC1 <- cbind(matMatrixC1, matrix(0, nrow = nrow(matMatrixC1), ncol = length(Cobj[[i]])))
}
}
}
dirC1 <- rep(">=", nRow)
rhsC1 <- rep(0, nRow)
csq <- list(matMatrixC1, dirC1, rhsC1)
names(csq) <- c("mat", "dir", "rhs")
csq
}
####################### 其他 ############################
SummaryCondition <- function(conditionList){
# 将所有的约束条件进行汇总
# Args:conditionList 约束条件列表
# return: 汇总后的, mat、rhs、dir。列表格式
mat <- NULL
rhs <- NULL
dir <- NULL
for(i in 1:length(conditionList)){
mat <- rbind(mat, conditionList[[i]]$mat)
dir <- c(dir, conditionList[[i]]$dir)
rhs <- c(rhs, conditionList[[i]]$rhs)
}
summary <- list(mat, dir, rhs)
names(summary) <- c("mat", "dir", "rhs")
summary
}