Multi-Precision Quantized Neural Networks via Encoding Decomposition of {-1，+1}

Multi-Precision Quantized Neural Networks via Encoding Decomposition of {-1，+1}

文章链接 2019年5月31日

Introduction

直接使用高bit模型的参数初始化低bit模型，因此训起来很快

提出了一系列的函数(MBitEncoder)来分解激活值，可直接用于inference阶段的计算。

做完分解之后，编码可直接存入1-bit的vectors。

Multi-Precision Quantized Neural Networks

Model Decomposition

CNN中矩阵乘法是最耗时的，非负数都可以用$\{0,1\}$来进行编码。用$x=[x^1,x^2,\dots ,x^N{]}^T$和$w=[w^1,w^2,\dots ,w^N{]}^T$来表示两个非负的向量，其中，$x^i,w^i\in \{0,1,2,\dots \}i=1,2,\dots ,N$，两个向量的点乘就可以表示如下：
$$\begin{array}{rl}{x}^T\cdot w& =\left[{\mathrm{x}}^1,{\mathrm{x}}^2,\dots ,{\mathrm{x}}^N\right]{\left[{\mathrm{w}}^1,{\mathrm{w}}^2,\dots ,{\mathrm{w}}^N\right]}^T\\ & =\sum _{n=1}^N{\mathrm{x}}^n\cdot {\mathrm{w}}^n\end{array}\text{\hspace{1em}(1)}$$上面的操作包括$N$次乘法和$N-1$次加法。如果用$0,1$来进行编码的话，则
$$x=[{\mathrm{c}}_M^1{\mathrm{c}}_{M-1}^1\cdots {\mathrm{c}}_1^1,{\mathrm{c}}_M^2{\mathrm{c}}_{M-1}^2\cdots {\mathrm{c}}_1^2,\dots ,{\mathrm{c}}_M^N{\mathrm{c}}_{M-1}^N\dots {\mathrm{c}}_1^N{]}^T\text{\hspace{1em}(2)}$$然后右边的可以转换为：
$$\left[\begin{array}{cccc}{\mathrm{c}}_M^1& {\mathrm{c}}_M^2& \cdots & {\mathrm{c}}_M^N\\ {\mathrm{c}}_{M-1}^1& {\mathrm{c}}_{M-1}^2& \cdots & {\mathrm{c}}_{M-1}^N\\ ⋮& ⋮& \cdots & ⋮\\ {\mathrm{c}}_1^1& {\mathrm{c}}_1^2& \cdots & {\mathrm{c}}_1^N\end{array}\right]=\left[\begin{array}{c}{c}_M\\ c_{M-1}\\ ⋮\\ c_1\end{array}\right]\text{\hspace{1em}(3)}$$其中：
$$x^j=\sum _{m=1}^M{2}^{m-1}\cdot c_m^j,c_m^j\in \{0,1\}\text{\hspace{1em}(4)}$$

$${\mathrm{c}}_i=[{\mathrm{c}}_i^1,{\mathrm{c}}_i^1,\dots ,{\mathrm{c}}_i^N]\text{\hspace{1em}(5)}$$

这样的话，用于表示数据的数量不会超过$2^M$。同样的，将$w$也使用$K$-bit编码，因此，上面的点乘就变成了
$$\begin{array}{rl}{x}^T\cdot w& =\sum _{n=1}^N{x}^n\cdot w^n\\ & =\sum _{n=1}^N(\sum _{m=1}^M{2}^{m-1}\cdot c_m^n)\cdot (\sum _{k=1}^K{2}^{k-1}\cdot d_k^n)\\ & =\sum _{m=1}^M\sum _{k=1}^K{2}^{m-1}\cdot 2^{k-1}\cdot c_m\cdot d_k^T\end{array}\text{\hspace{1em}(6)}$$由上可知，点乘被分解成$M\times K$个子运算，其中，每个运算的元素都是0或1。然而，上面的这种形式只能表示非负数，而weight和activation不一定都是非负的。

为了扩展编码空间，使用$\{-1,+1\}$代替$\{0,1\}$作为编码的基本元素，编码的规则是一样的：
$$x^i=\sum _{m=1}^M{2}^{m-1}\cdot c_m^i,c_m^i\in \{-1,1\}\text{\hspace{1em}(7)}$$式中，$M$表示编码的bit位数，共能表示$2^M$种值。

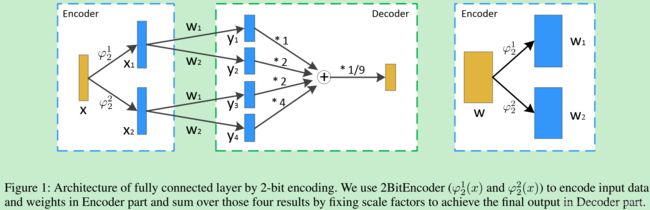
上图中，使用2-bit进行编码。$x$是输入数据，$w$是权重矩阵，这里假定不存在bias。然后定义一个“Encoder”，便于在2BitEncoder function ${\phi }_2^1(\cdot )$和${\phi }_2^2(\cdot )$中使用，这个是用于对输入进行编码。例如，$x$可以用$x_1\in \{-1,+1{\}}^N$和$x_2\in \{-1,+1{\}}^N$编码，其中，$x_1$表示低bit数据，$x_2$表示高bit数据，$x=x_1+2x_2$。同样的，$w$可以进行编码为$w_1\in \{-1,+1{\}}^{M\times N}$和$w_2\in \{-1,+1{\}}^{M\times N}$。经过交叉相乘之后，得到了四个中间变量$\{y_1,y_2,y_3,y_4\}$。每一个乘法都可以认为是二进制下的全连接层，这种分解可以看成有很多分支的层，因此称之为Multi-Branch Binary Networks (MBNs)

M-bit Encoding Functions

神经网络的一个重要特性就是非线性。在本论文中，encoding function扮演了很重要的角色。一般的QNN中，并没有明确给出quantized numbers和encode bits之间的仿射变换，本部分提出了一些$M$-bit的encoding function。

在量化之前，数据应该被线性在一个固定的数值范围内。使用了一个叫$HReLU(\cdot )$的激活函数，便于更快地使用SGD收敛，并把输入值限制在$[0,1]$。
$$H\mathrm{Re}LU(x)=\{\begin{array}{ll}+1,& x>1\\ x,& 0⩽x⩽1\\ 0,& x⩽0\end{array}\text{\hspace{1em}(8)}$$ $M$-bit的encoding function的输出也应该是$M$个-1或者+1的数，这些数就表示了输入的编码，然后点乘就可以用式$(6)$进行计算。同时，在上面那个图中，用2-bit来编码$x$并把它限制在$[-1,1]$，这样就会有4种编码状态。如下表2所示。

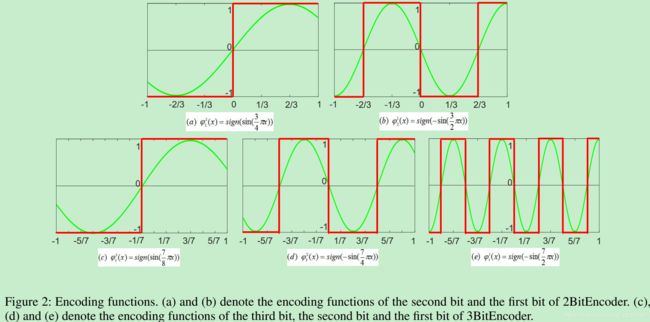
在表2中，是有一个线性的因子$\alpha$的。对于表2来说，$\alpha =3$。再用式$(6)$计算的话，这个值就会变成${\alpha }^2$倍。因此，在图1中就会产出一个$1/9$。图2说明了2-bit和3-bit的编码函数，可以看到这些编码函数必须是周期性的，每个函数有不同的周期。自然地，我们会使用三角函数作为基本的encoder function，编码方式用红线标出。其数学表达如下：
$$2BitEncoder(x)=\{\begin{array}{c}{\phi }_2^2(x):\text{sign}(\sin (\frac{3}{4}\pi x)),\\ {\phi }_2^1(x):\text{sign}(-\sin (\frac{3}{2}\pi x))\end{array}\text{\hspace{1em}(9)}$$式中，${\phi }_2^1(x)$表示2BitEncoder中的第一个bit的encoding function，${\phi }_2^2(x)$表示2BitEncoder中的第二个bit的encoding function，它们两的周期明显是不同的。

Networks Training

对于QNN来说，由于导数没有定义，无法使用传统的梯度优化算法进行求解。不同的论文提出的不同的方法解决这个问题。

Multi-Branch Binary Networks Training

MBNs需要使用$M$-bit的encoding function得到每个bit为的元素，从而使得运算更加高效。它的训练方式用2-bit进行举例说明。由于编码中符号函数的存在使得直接使用BP变得困难，我们使用下面的方式近似计算encoder function的导数。
$$\frac{\partial {\phi }_2^2(x)}{\partial x}=\{\begin{array}{cc}\frac{3}{4}\pi \cos \left(\frac{3}{4}\pi x\right),& -1⩽x⩽1\\ 0& \text{ otherwise }\end{array}\text{\hspace{1em}(10)}$$

$$\frac{\partial {\phi }_2^1(x)}{\partial x}=\{\begin{array}{cc}-\frac{3}{2}\pi \cos \left(\frac{3}{2}\pi x\right),& -1⩽x⩽1\\ 0& \text{ otherwise }\end{array}\text{\hspace{1em}(11)}$$

除了激活值，网络中所有的权重也必须二值化。在训练过程中保留实值权重$w$和二值化权重$w_b$，使用$w_b$来计算loss和梯度，来更新$w$。$w$被限制在-1和1之间，防止出现excessive growth。不同与权重，$w$的二值化函数对于encoding function来说并不需要，直接定义为：
$$Binarize(x)=sign(HTanh(x))\text{\hspace{1em}(12)}$$对于这个函数，我们定义了每个元素的梯度函数来限制搜索空间，也就是说，sign函数的输入被$HTanh(x)$限定在$[-1,+1]$之间，它也能加速收敛。

Quantized Networks Training

上述的训练方式是用于训练二值网络的，也可以转换到多值网络中。只不过，转换会产生很多的参数。如果只优化二值化网络的话，又容易陷入局部最优解。因此直接优化多bit的量化网络，并在inference阶段使用multi-branch binary operations。一般有两种量化方法：linear quantization and logarithmic quantization。鉴于编码机制，我们使用linear quantization，定义如下：
$$q_k(x)=2\left(\frac{<\left(2^k-1\right)\left(\frac{x+1}{2}\right)>}{2^k-1}-\frac{1}{2}\right)\text{\hspace{1em}(13)}$$式中，$<\cdot >$表示rounding operation，将一个实数$x\in [-1,+1]$量化。也是使用STE加速计算，使用量化的参数计算loss并更新全精度的参数。对于使用low-precision的量化编码方案，使用Adam训练，其他情况使用SGD训练。

Experiments

本文中，在训1-bit的时候使用$HTanh(\cdot )$作为激活函数，其他情况使用$HReLU(\cdot )$，编码bit为1或者2时，使用Adam收敛更快，当编码数不低于3的时候，使用SGD，学习率设为0.1。在ImageNet上性能表现如下表3。

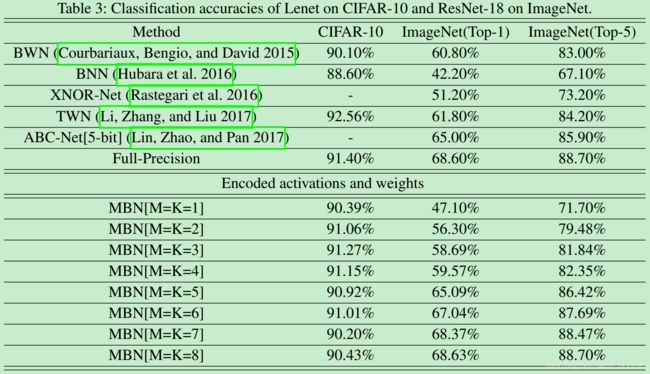
总得来说，不是精度高，就是精度差不多，但速度更快。同时它的编码方式多样。对于目标检测的结果如下表4所示：

Discussion and Conclusion

{0,1} Encoding and {-1，+1} Encoding

一般而言，映射的方式为：
$${\mathrm{x}}^q=\frac{2}{2^M-1}{\mathrm{x}}^{\{0,1\}}-1\text{\hspace{1em}(14)}$$式中，$x^q$表示量化的值，$x^{\{0,1\}}$表示用0和1编码的固定点整数，$K$-bit固定点整数表示一个量化的数值$w^q$，乘积就可以表示为：
$$\begin{array}{rl}{\mathrm{x}}^q\cdot {\mathrm{w}}^q=& \frac{4}{\left(2^M-1\right)\left(2^K-1\right)}{\mathrm{x}}^{\{0,1\}}\cdot {\mathrm{w}}^{\{0,1\}}-\\ & \frac{2}{2^M-1}{\mathrm{x}}^{\{0,1\}}-\frac{2}{2^K-1}{\mathrm{w}}^{\{0,1\}}+1\end{array}\text{\hspace{1em}(15)}$$上式右边是一个多项式，有四项，每一项都有自己的尺度因子，${\mathrm{x}}^{\{0,1\}}\cdot {\mathrm{w}}^{\{0,1\}}$可以使用bitwise操作加速，然而，多项式和尺度因子的计算会增加计算的复杂度。对于本文提出的二值量化编码方案，两个数的乘积被表示为
$$\begin{array}{rl}{\mathrm{x}}^q\cdot {\mathrm{w}}^q=& \frac{1}{\left(2^M-1\right)\left(2^K-1\right)}{\mathrm{x}}^{\{-1,1\}}\cdot {\mathrm{w}}^{\{-1,1\}}\end{array}\text{\hspace{1em}(16)}$$式中，${\mathrm{x}}^{\{-1,1\}}$和${\mathrm{w}}^{\{-1,1\}}$表示用-1和1编码的固定点整数，显然，这种计算方式是更加高效的。

Linear Approximation and Quantization

ABC网络中使用了$K$个二进制编码的权重子集$\{{\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_K\}$来逼近权重$\mathrm{w}$，其中${\mathrm{w}}_i\in \{-1,+1{\}}^N$，然后就能用bitsiwe操作加速，但是还必须解下面这个问题：
$$\underset{{\left\{{\alpha }_i,w_i\right\}}_{i=1}^K}{\min }{\Vert w-\sum _{i=1}^K{\alpha }_i{w}_i\Vert }^2,w\in {\mathbb{R}}^N\text{\hspace{1em}(17)}$$在使用的时候，$w_i$可以看作网络的权重，但是会引入尺度因子${\alpha }_i$，把参数量扩大$K$倍，因此这种方法把原始的二值网络变复杂，很难训，容易陷入局部最优解。

本论文中，使用${\mathrm{w}}^q$来逼近$\mathrm{w}$：
$$\mathrm{w}\approx \frac{1}{2^K-1}{\mathrm{w}}^q,w\in [-1,1{]}^N\text{\hspace{1em}(18)}$$式中，${\mathrm{w}}^q$是一个或正或负的奇数，且它的绝对值不大于$2^K-1$，相对于上面的方案，这种方案更能够直接得到量化的权重。