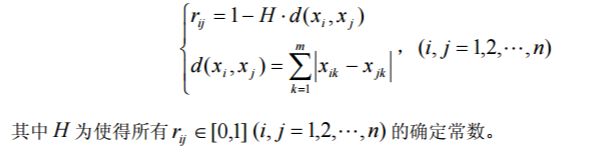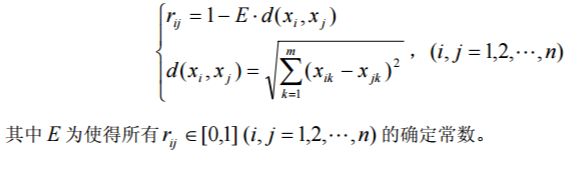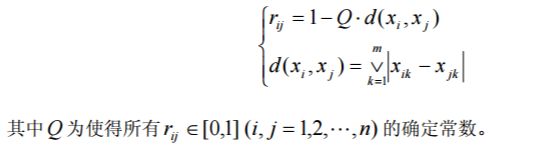模糊聚类分析方法

---

模糊数学模型系列博文：

【1】基本概念： 隶属函数、模糊集合的表示方法、模糊关系、模糊矩阵

【2】模糊模式识别：海明贴近度 、欧几里得贴近度 、黎曼贴近度、 格贴近度、最大隶属原则、择近原则

【3】模糊聚类分析方法：模糊等价矩阵、模糊相似矩阵、传递闭包法、布尔矩阵法

【4】模糊决策分析方法

---

在工程技术和经济管理中，常常需要对某些指标按照一定的标准(相似的程度或亲 疏关系等)进行分类处理。例如，根据生物的某些性态对其进行分类，根据空气的性质 对空气质量进行分类，以及工业上对产品质量的分类、工程上对工程规模的分类、图像 识别中对图形的分类、地质学中对土壤的分类、水资源中的水质分类等等。这些对客观 事物按一定的标准进行分类的数学方法称为聚类分析，它是多元统计“物以聚类”的一种分类方法。然而，在科学技术、经济管理中有许多事物的类与类之间并无清晰的划分， 边界具有模糊性，它们之间的关系更多的是模糊关系。对于这类事物的分类，一般用模糊数学方法、我们把应用模糊数学方法进行的聚类分析，称为模糊聚类分析。

---

目录

1 预备知识

1.1 模糊等价矩阵                       n 阶等价布尔矩阵                           模糊分类

1.2 模糊相似矩阵

2 模糊聚类分析法的基本步骤

(1) 获取数据

(2) 数据的标准化处理             ① 平移—标准差变换                        ② 平移—极差变换

Step2: 建立模糊相似矩阵

(1) 数量积法                                            (2) 夹角余弦法

(3) 相关系数法                                         (4) 指数相似系数法

(5) 最大最小值法                                     (6) 算术平均值法

(7) 几何平均值法                                     (8) 绝对值倒数法

(9) 绝对值指数法                                     (10) 海明距离法

(11) 欧氏距离法                                      (12) 切比雪夫距离法

(13) 主观评分法

Step3: 聚类

(1) 传递闭包法                (2) 布尔矩阵法              (3) 直接聚类法

3 模糊聚类分析应用案例

（1）建立模糊集合                                  （2）利用格贴近度建立模糊相似矩阵

（3）求 R 的传递闭包                             （4）选择保留观测站的准则

---

---

1 预备知识

1.1 模糊等价矩阵

 

n 阶等价布尔矩阵

模糊分类

 

1.2 模糊相似矩阵

 

2 模糊聚类分析法的基本步骤

Step1: 数据标准化

(1) 获取数据

(2) 数据的标准化处理

在实际问题中，不同的数据可能有不同的性质和不同的量纲，为了使原始数据能够 适合模糊聚类的要求，需要将原始数据矩阵 A 作标准化处理，即通过适当的数据变换，将其转化为模糊矩阵。常用的方法有以下两种：

① 平移—标准差变换

② 平移—极差变换

Step2: 建立模糊相似矩阵

(1) 数量积法

(2) 夹角余弦法

(3) 相关系数法

(4) 指数相似系数法

(5) 最大最小值法

                  式中 ∧ 为取小运算min，∨ 代表取大运算max

(6) 算术平均值法

(7) 几何平均值法

(8) 绝对值倒数法

(9) 绝对值指数法

(10) 海明距离法

(11) 欧氏距离法

(12) 切比雪夫距离法

(13) 主观评分法

Step3: 聚类

所谓聚类方法就是依据模糊矩阵将所研究的对象进行分类的方法。对于不同的置信 水平λ ∈[0,1]，可以得到不同的分类结果，从而形成动态聚类图。常用的方法如下：

(1) 传递闭包法

从 Step2 中求出的模糊相似矩阵 R 出发，来构造一个模糊等价矩阵  。其方法就 是用平方法求出 R 的传递闭包t(R) ，则  t(R) =  ；然后，由大到小取一组λ ∈[0,1] ， 确定相应的λ 截矩阵，则可以将其分类，同时也可以构成动态聚类图。

(2) 布尔矩阵法

(3) 直接聚类法

此方法是直接由模糊相似矩阵求出聚类图的方法，具体步骤如下：

3 模糊聚类分析应用案例

例 15 某地区内有 12 个气象观测站，10 年来各站测得的年降水量如表 3 所示。 为了节省开支，想要适当减少气象观测站，试问减少哪些观察站可以使所得到的降水量 信息仍然足够大？

解 我们把 12 个气象观测站的观测值看成 12 个向量组，由于本题只给出了 10 年 的观测数据，根据线性代数的理论可知，若向量组所含向量的个数大于向量的维数，则 该向量组必然线性相关。于是只要求出该向量组的秩就可确定该向量组的最大无关组所 含向量的个数，也就是需保留的气象观测站的个数。由于向量组中的其余向量都可由极 大线性无关组线性表示，因此，可以使所得到的降水信息量足够大。

到目前为止，问题似乎已经完全解决了，可其实不然，因为如果上述观测站的数 据不是 10 年，而是超过 12 年，则此时向量的维数大于向量组所含的向量个数，这样的 向量组未必线性相关。故上述的解法不具有一般性，下面我们考虑一般的解法，首先， 我们利用已有的 12 个气象观测站的数据进行模糊聚类分析，最后确定从哪几类中去掉 几个观测站。

（1）建立模糊集合

（2）利用格贴近度建立模糊相似矩阵

（3）求 R 的传递闭包

其余观测站属于中间水平。

（4）选择保留观测站的准则

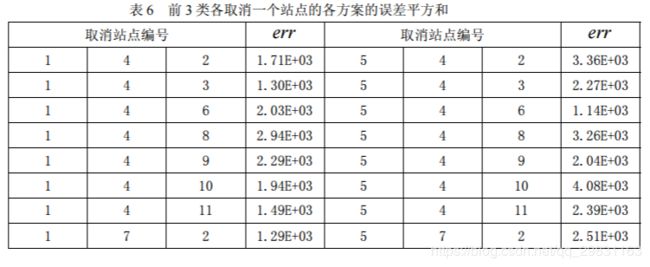
显然，去掉的观测站越少，则保留的信息量越大。为此，我们考虑在去掉的观测 站数目确定的条件下，使得信息量最大的准则。由于该地区的观测站分为 4 类，且第 4 类只含有一个观测站，因此，我们从前 3 类中各去掉一个观测站，我们的准则如下：

（5）求解的 MATLAB 程序如下：

i）求模糊相似矩阵的 MATLAB 程序

a=[276.2 324.5 158.6 412.5 292.8 258.4 334.1 303.2 292.9 243.2 159.7 331.2
251.5 287.3 349.5 297.4 227.8 453.6 321.5 451.0 466.2 307.5 421.1 455.1
192.7 433.2 289.9 366.3 466.2 239.1 357.4 219.7 245.7 411.1 357.0 353.2
246.2 232.4 243.7 372.5 460.4 158.9 298.7 314.5 256.6 327.0 296.5 423.0
291.7 311.0 502.4 254.0 245.6 324.8 401.0 266.5 251.3 289.9 255.4 362.1
466.5 158.9 223.5 425.1 251.4 321.0 315.4 317.4 246.2 277.5 304.2 410.7
258.6 327.4 432.1 403.9 256.6 282.9 389.7 413.2 466.5 199.3 282.1 387.6
453.4 365.5 357.6 258.1 278.8 467.2 355.2 228.5 453.6 315.6 456.3 407.2
158.2 271.0 410.2 344.2 250.0 360.7 376.4 179.4 159.2 342.4 331.2 377.7
324.8 406.5 235.7 288.8 192.6 284.9 290.5 343.7 283.4 281.2 243.7 411.1];
mu=mean(a),sigma=std(a)
for i=1:12
    for j=1:12
        r(i,j)=exp(-(mu(j)-mu(i))^2/(sigma(i)+sigma(j))^2);
    end
end
r
save data1 r a

ii）矩阵合成的 MATLAB 函数

function rhat=hecheng(r);
n=length(r);
for i=1:n
    for j=1:n
        rhat(i,j)=max(min([r(i,:);r(:,j)']));
    end
end

iii）求模糊等价矩阵和聚类的程序

load data1
r1=hecheng(r)
r2=hecheng(r1)
r3=hecheng(r2)
bh=zeros(12);
bh(find(r2>0.998))=1 

iv)计算表6的程序  编写计算误差平方和的函数如下：

function err=wucha(a,t);
b=a;b(:,t)=[];
mu1=mean(a,2);mu2=mean(b,2);
err=sum((mu1-mu2).^2);

计算28个方案的主程序如下：

load data1
ind1=[1,5];ind2=[2:3,6,8:11];ind3=[4,7];
so=[];
for i=1:length(ind1)
    for j=1:length(ind3)
        for k=1:length(ind2)
            t=[ind1(i),ind3(j),ind2(k)];
            err=wucha(a,t);
            so=[so;[t,err]];
        end
    end
end
so
tm=find(so(:,4)==min(so(:,4)));
shanchu=so(tm,1:3)

---

模糊数学模型系列博文：

【1】基本概念： 隶属函数、模糊集合的表示方法、模糊关系、模糊矩阵

【2】模糊模式识别：海明贴近度 、欧几里得贴近度 、黎曼贴近度、 格贴近度、最大隶属原则、择近原则

【3】模糊聚类分析方法：模糊等价矩阵、模糊相似矩阵、传递闭包法、布尔矩阵法

【4】模糊决策分析方法

---