模糊决策分析方法

---

模糊数学模型系列博文：

【1】基本概念： 隶属函数、模糊集合的表示方法、模糊关系、模糊矩阵

【2】模糊模式识别：海明贴近度 、欧几里得贴近度 、黎曼贴近度、 格贴近度、最大隶属原则、择近原则

【3】模糊聚类分析方法：模糊等价矩阵、模糊相似矩阵、传递闭包法、布尔矩阵法

【4】模糊决策分析方法

---

模糊数学中有一个研究的热点问题就是“模糊决策”，它就是研究在模糊环境下或者 模糊系统中进行决策的数学理论和方法。模糊决策的目标是把决策论域中的对象在模糊 环境下进行排序，或按某些模糊限制条件从决策域中选择出最优对象。

---

目录

1 模糊综合评价法                           ★ 多目标模糊综合评价法建模实例

2 多目标模糊综合评价决策法         ★ 多目标模糊综合评价决策法建模实例

3 多层次模糊综合评价模型的数学方法

3.1 多层次模糊综合评价模型数学方法的基本步骤

3.2 多目标模糊综合评价决策法建模实例

（4）权重的确定        ① 频数统计法确定权重.              ② 模糊层次分析法（AHP）确定权重

          4 模糊多属性决策方法                                                           4.1 模糊多属性决策理论的描述

4.2 折衷型模糊多属性决策方法                                           （2）折衷型模糊决策的基本步骤

Step1：指标数据的三角形模糊数表达                         Step2: 模糊指标矩阵 F 归一化处理

Step3: 构造模糊决策矩阵                                            Step4: 确定模糊正理想 与模糊负理想 

4.3 折衷型模糊决策方法建模实例

---

---

1 模糊综合评价法

模糊综合评价方法，是应用模糊关系合成的原理，从多个因素(指标)对被评价事物 隶属等级状况进行综合性评判的一种方法，其具体的步骤为:

常用的模糊算子有:

经过比较研究， M (•,⊕) 对各因素按权数大小，统筹兼顾，综合考虑，比较合理。

(6) 对模糊综合评价结果 B 作分析处理。

★ 多目标模糊综合评价法建模实例

科技成果通常可用技术水平、技术难度、工作量、经济效益、社会效益等 5 个指 标进行评价，等级分为一等、二等、三等、四等。某项科研成果经过评委会评定，得到 单因素评判矩阵.

用 M (•,⊕) 算子，得 B = (0.23,0.35,0.31,0.11) 由计算结果可见，用 M (•,⊕) 评价模型比较合理，成果应评为二等奖。

2 多目标模糊综合评价决策法

当被评价的对象有两个以上时，从多个对象中选择出一个最优的方法称为多目标模 糊综合评价决策法。 评价的步骤：

① 对每个对象按上面多个目标（因素）进行模糊综合评价；

② 将模糊评语量化，计算各对象的优先度。假设模糊评价评语量化集（或评价尺 度）为 S ，则各对象的优先度为：

★ 多目标模糊综合评价决策法建模实例

假定在上例中有两项科研成果，第一项科研成果为甲项，其模糊评价结果为 B1 = (0.23,0.5,0.31,0.11) 现对科研成果乙进行同样的模糊评价，其评价矩阵为

各评价因素的权值分配为 A = (0.35,0.35,0.1,0.1,0.1)

所以，综合评价为

 例 16 某露天煤矿有五个边坡设计方案，其各项参数根据分析计算结果得到边坡 设计方案的参数如下表所示。

据勘探该矿探明储量 8800 吨，开采总投资不超过 8000 万元，试作出各方案的优 劣排序，选出最佳方案。 解 首先确定隶属函数：

（1）可采矿量的隶属函数

因为勘探的地质储量为 8800 吨，故可用资源的利用函数作为隶属函数

根据专家评价，诸项目在决策中占的权重为 A = (0.25, 0.20, 0.20, 0.10, 0.25) ， 于是得诸方案的综合评价为 B = AR = (0.7435, 0.5919, 0.6789, 0.3600, 0.3905)

由此可知：方案 I 最佳，III 次之，IV 最差。 程序计算如下：

（1）首先编写函数文件 myfun.m 如下：

function f=myfun(x);
f(1,:)=x(1,:)/8800;
f(2,:)=1-x(2,:)/8000;
f(3,:)=0;
f(3,find(x(3,:)<=5.5))=1; 
flag=find(x(3,:)>5.5 & x(3,:)<=8);
f(3,flag)=(8-x(3,flag))/2.5;
f(4,:)=1-x(4,:)/200;
f(5,:)=(x(5,:)-50)/1450; 

（2）编写程序文件如下：

x=[4700 6700 5900 8800 7600
5000 5500 5300 6800 6000
4.0 6.1 5.5 7.0 6.8
30 50 40 200 160
1500 700 1000 50 100];
r=myfun(x);
a=[0.25,0.20,0.20,0.10,0.25];
b=a*r 

3 多层次模糊综合评价模型的数学方法

3.1 多层次模糊综合评价模型数学方法的基本步骤

3.2 多目标模糊综合评价决策法建模实例

科技成果模糊综合评价模型的建立及其有关参数的确定。

（1）科技成果综合评价的因素集(指标体系)的确定 根据科研成果的特点， 并经过专家调研， 设计以下一套综合评价指标体系.

（2）科技成果的评语集的确定

在评价科技成果时，可以将其分为一定的等级. 在此， 从“专家打分”的角度把 评价的等级分为“10 分”、“8 分”、“6 分”、“4 分”、“2 分”五个等级，因此评语集表 示为： V = {10 分， 8 分， 6 分， 4 分， 2 分}.

（4）权重 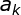 的确定

在（1）给出的综合评价体系中三大准则及 9 个指标中， 他们在综合评价中的重要 程度是不一样的。地位重要的，应给予较大的权重；反之，应给出较小的权重。下文给 出两种确定权重的实用方法。

① 频数统计法确定权重.

② 模糊层次分析法（AHP）确定权重

该法的基本原理是从（1）中给出的综合评价体系的层次结构出发，针对每个准则 内的指标，运用专家的知识、智慧、信息和价值观，对同一层或同一个域的指标进行两 两比较对比，并按 1—9 判断标度及含义构造判断矩阵 D = ，再由组织者计算比

（5）科技成果的综合评价

4 模糊多属性决策方法

4.1 模糊多属性决策理论的描述

4.2 折衷型模糊多属性决策方法

（1）折衷型模糊决策的基本原理 折衷型模糊决策的基本原理是：

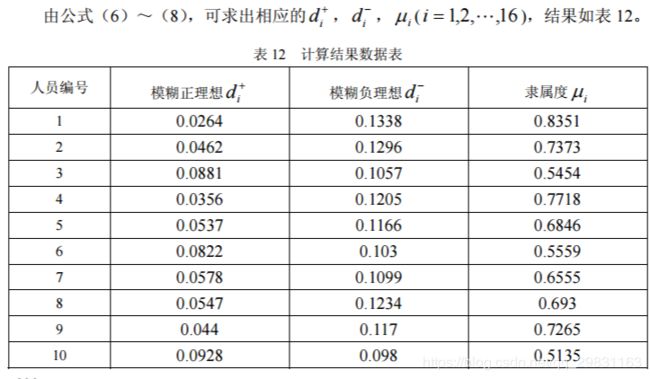
从原始的样本数据出发，先虚拟模糊正理想和模糊 负理想，其中模糊正理想是由每一个指标中模糊指标值的极大值构成；模糊负理想是由 每一个指标中模糊指标值的极小值构成。然后采用加权欧氏距离的测度工具来计算各备 选对象与模糊正理想和模糊负理想之间的距离。在此基础上，再计算各备选对象属于模 糊正理想的隶属度，其方案优选的原则是，隶属度越大，该方案越理想。

（2）折衷型模糊决策的基本步骤

Step1：指标数据的三角形模糊数表达

下面运用以上的定义将定性、定量指标以及权重数据统一量化为三角形模糊数.

1) 对于定性指标，可以将两极比例法改进为三角模糊数比例法。再利用三角模糊 数比例法将定性指标转化为定量指标，其具体的转化形式见表 9。

2) 对于精确的定量指标值，也写成三角模糊数的形式。设 a 是一个具体的精确数， 由三角模糊数的定义，则 a 表示成三角模糊数的形式为：

数的表达形式.

Step2: 模糊指标矩阵 F 归一化处理

Step3: 构造模糊决策矩阵

Step4: 确定模糊正理想 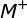与模糊负理想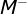 

设

4.3 折衷型模糊决策方法建模实例

某市直属单位因工作需要，拟向社会公开招聘 8 名公务员，具体的招聘办法和程序 如下：

（一）公开考试：凡是年龄不超过 30 周岁，大学专科以上学历，身体健康者均可 报名参加考试，考试科目有：综合基础知识、专业知识和“行政职业能力测验”三个部 分，每科满分为 100 分。根据考试总分的高低排序选出 16 人选择进入第二阶段的面试 考核。

（二）面试考核：面试考核主要考核应聘人员的知识面、对问题的理解能力、应变 能力、表达能力等综合素质。按照一定的标准，面试专家组对每个应聘人员的各个方面 都给出一个等级评分，从高到低分成 A/B/C/D 四个等级，具体结果见表 10 所示。

现要求根据表 8 中的数据信息对 16 名应聘人员作出综合评价，选出 8 名作为录用 的公务员。

建模过程：

① 借鉴表 9 的思想，对于定性指标值 A，B，C，D，可以定义表 10 的量化标准 将这些定性指标进行量化，其具体的量化形式见表 11。

② 由表 11 和公式（1）把表 10 中的指标信息、权重信息化成三角形模糊数，得到

③ 由公式（3’）和（4）将 F 中的数据进行归一加权化，得到模糊决策矩阵 D 。

④ 由公式（5）确定出模糊正理想与模糊负理想

⑤ 模糊优选决策

因此被选种的 8 个人员是人员 1、4、2、9、8、5、7、12。 计算的 MATLAB 程序如下：

%把表 3 中的数据复制到纯文本文件 mohu.txt 中，然后把 A 替换成 85 90 100，
%B 替换成 75 80 85，C 替换成 60 70 75，D 替换成 50 55 60
clc,clear
load mohu.txt
sj=[repmat(mohu(:,1),1,3),mohu(:,2:end)];
%首先进行归一化处理
n=size(sj,2)/3;m=size(sj,1);
w=[0.5*ones(1,3),0.125*ones(1,12)];
w=repmat(w,m,1);
y=[];
for i=1:n
    tm=sj(:,3*i-2:3*i);
    max_t=max(tm);
    max_t=repmat(max_t,m,1);
    max_t=max_t(:,3:-1:1);
    yt=tm./max_t;yt(:,3)=min([yt(:,3)';ones(1,m)]);
    y=[y,yt];
end
%下面求模糊决策矩阵
r=[];
for i=1:n
    tm1=y(:,3*i-2:3*i);tm2=w(:,3*i-2:3*i);
    r=[r,tm1.*tm2];
end
%求 M＋、M－和距离
mplus=max(r);mminus=min(r)
dplus=dist(mplus,r');dminus=dist(mminus,r');
%求隶属度
mu=dminus./(dplus+dminus);
[mu_sort,ind]=sort(mu,'descend') 

习题

1. （工程评标问题）某建设单位组织一项工程项目的招标，现组建成评标专家组 对 4 个投标单位的标书进行评标。4 个标书的指标信息见表 13，其中前三个指标信息是 各投标单位给定的精确数据，后三个指标信息是评标专家组经考察后的定性结论。 请 你帮评标专家组设计一个工程评标模型，以确定最后中标单位.

---

模糊数学模型系列博文：

【1】基本概念： 隶属函数、模糊集合的表示方法、模糊关系、模糊矩阵

【2】模糊模式识别：海明贴近度 、欧几里得贴近度 、黎曼贴近度、 格贴近度、最大隶属原则、择近原则

【3】模糊聚类分析方法：模糊等价矩阵、模糊相似矩阵、传递闭包法、布尔矩阵法

【4】模糊决策分析方法

---