遗传算法详解
所有博文已迁移至个人网站:https://www.ravenxrz.ink,请勿再留言评论
新链接:https://www.ravenxrz.ink/archives/8df54bf5.html
文章目录
- 1.遗传算法基本原理
- 1.1遗传算法基础
- 1.2遗传算法实现步骤
- 1.编码
- 2.解码
- 3.交配
- 4.突变
- 5.倒位
- 6.个体适应度评估
- 7.复制
- 2.遗传算法的MATLAB程序设计
- 2.1程序设计流程及参数选取
- 1.伪代码
- 2.遗传算法的参数设计原则
- 3.遗传算法适应度函数设计
- 3.遗传算法应用案例
1.遗传算法基本原理
1.1遗传算法基础
种群是生物进化的基本单位的,生物进化的实质是种群基本频率的改变。基因突变和基因重组、自然选择以及隔离是物种形成过程中的三个基本环节,通过他们的综合作用,种群产生分化,最终导致新物种的形成。
1.2遗传算法实现步骤
1.编码
遗传算法的编码有浮点编码和二进制编码两种。这里介绍为禁止编码。设某一参数的取值范围为 ( L , U ) (L,U) (L,U),使用长度为k的二进制编码表示改参数,则它共有 2 k 2^k 2k中不同的编码,每相邻的编码的两个编码的间隔是 Δ \Delta Δ,容易知道
Δ = ( U − L ) ( 2 k − 1 ) \Delta= \frac{(U-L)}{(2^k-1)} Δ=(2k−1)(U−L)
2.解码
解码的目的就是将不直观的二进制数据串还原成十进制。
遗传算法的编码和解码在宏观上可以对应生物的基因型和表现型,在围观上可以对应DNA的转录和翻译两个过程。
3.交配
“交配运算”是使用单点或者多点进行交叉的算子。首先用随机数产生一个或者多个叫叫配电的位置,然后两个个题在叫配电位置互换部分基因码,形成两个子个体。如下图:
两个基因在"/"处进行了交换
4.突变
“突变运算”是使用基本位进行基因突变 。例如,将染色体S=11001101第3位上的0变为1,即S = 11101101=S’.S’可以被看做是原染色S的子代染色体。
5.倒位
将染色体基因的一部分进行逆序排列。例如:S = 100/1100/11,倒位以后为S’ = 100/0011/11.
6.个体适应度评估
遗传算法依照与个体适应度成正比的几率决定当前种群中各个个体遗传都下一代群体中的机会。通常求目标函数最大值的问题可以直接把目标函数作为检测个体适应度大小的函数。
7.复制
复制运算时根据个体适应度大小决定其下代遗传的可能性。弱设种群中个体总数为N,个体i的适应度为fi,则个体i被选取的几率为:
P i = f i 总 适 应 度 Pi = \frac{f_i}{总适应度} Pi=总适应度fi
2.遗传算法的MATLAB程序设计
2.1程序设计流程及参数选取
1.伪代码
% 遗传算法的伪代码
BEGIN
t = 0; %遗传代数
初始化P(t);%初始化种群或者染色体
计算P(t)的适应值;
while(不满足停止准则) do
begin
t = t+1;
从P(t-1)中选择P(t); %选择
重组P(t);
计算P(t)的适应值;
end
end
END
2.遗传算法的参数设计原则
1.种群的规模
种群不宜过大也不宜过小。种群规模的一个建议值为0-100。
2.变异概率
变异概率也不宜过大或者过小。一般取值为0.0001-0.2
3.交配概率
同上,不宜过大或者过小。一般取值 为0.4-0.99
4.进化代数
同上,不宜过大或者过小。一般取值为100-500。
5.种群初始化
初始种群的生成是随机的。在出是种群的赋予之前,尽量进行一个大概的区间估计,避免初始种群分布在远离最优解的编码空间,导致遗传算法的搜索范围受到限制。
3.遗传算法适应度函数设计
1.遗传算法和直接搜索工具箱中的函数ga是求解目标函数的最小值,所以如果目标函数为求解最小值,则直接令目标函数为适应度函数即可。编写的适应度函数,语法如下:
function f = fitnesscn(x)
f = f(x);
end
2.如果有约束条件(包括自变量的取值范围),对于求解函数的最小值问题,语法如下:
function f = fitnessfcx(x)
if x<=-1||x>3
f = inf;
else
f = f(x);
end
end
3.如果有约束条件(包括自变量的取值范围),对于求解函数的最大值问题,语法如下:
function f = fitnessfcx(x)
if x<=-1||x>3
f = inf;
else
f = -f(x);
end
end
注意:最后求解出来的目标函数为-fval而不是fval
3.遗传算法应用案例
这里给出三个案例。
案例一:无约束目标函数的最大值
求解 m a x f ( x ) = 200 ∗ e ( − 0.05 x ) ∗ s i n x ; x ∈ [ − 2 , 2 ] max f(x) = 200*e^{(-0.05x)}*sinx ;x∈[-2,2] maxf(x)=200∗e(−0.05x)∗sinx;x∈[−2,2]
% 案例一:无约束目标函数的最大值
% 求解maxf(x)=200*e(−0.05x)*sinx; x∈[−2,2]
%主程序:用遗传算法求解y=200*exp(-0.05*x).*sin(x)在[-2 2]区间上的最大值
clc;
clear ;
close all;
global BitLength
global boundsbegin
global boundsend
bounds=[-2 2];%一维自变量的取值范围
precision=0.0001; %运算精度
boundsbegin=bounds(:,1);
boundsend=bounds(:,2);
%计算如果满足求解精度至少需要多长的染色体
BitLength=ceil(log2((boundsend-boundsbegin)' ./ precision));
popsize=50; %初始种群大小
Generationnmax=12; %最大代数
pcrossover=0.90; %交配概率
pmutation=0.09; %变异概率
%产生初始种群
population=round(rand(popsize,BitLength));
%计算适应度,返回适应度Fitvalue和累积概率cumsump
[Fitvalue,cumsump]=fitnessfun(population);
Generation=1;
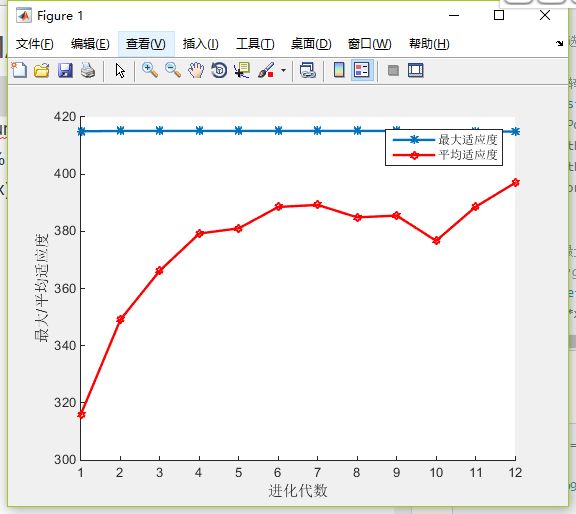
while Generation程序结果:
Bestpopulation =
1.575677119096666
Besttargetfunvalue =
1.848457326200009e+02
%主程序:本程序采用遗传算法接力进化,
%将上次进化结束后得到的最终种群作为下次输入的初始种群
clc;
close all;
clear all;
%进化的代数
T=100;
optionsOrigin=gaoptimset('Generations',T/2);
[x,fval,reason,output,final_pop]=ga(@ch14_2f,2,optionsOrigin);
%进行第二次接力进化
options1=gaoptimset('Generations',T/2,'InitialPopulation',final_pop,...
'PlotFcns',@gaplotbestf);
[x,fval,reason,output,final_pop]=ga(@ch14_2f,2,options1);
Bestx=x
BestFval=fval
%子函数:适应度函数同时也是目标函数,函数存储名称为ch14_2f.m
function f=ch14_2f(x)
g1=1.5+x(1)*x(2)-x(1)-x(2);
g2=-x(1)*x(2);
if (g1>0||g2>10)
f=100;
else
f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
end
end
程序结果:
Optimization terminated: maximum number of generations exceeded.
Optimization terminated: maximum number of generations exceeded.
Bestx =
-9.026449478668987 1.105769708316651
BestFval =
0.035051699473142
>>
案例三:经典TSP问题
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
% 利用遗传算法,解决TSP问题模板
tic
clc,clear
sj = load('yichuansuanfadata.txt'); %加载敌方100 个目标的数据
x=sj(:,1:2:8);x=x(:);
y=sj(:,2:2:8);y=y(:);
sj=[x y];
figure(1);
plot(x,y);
d1=[70,40];
sj0=[d1;sj;d1];
%距离矩阵d
sj=sj0*pi/180;
d=zeros(102);
for i=1:101
for j=i+1:102
temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
d(i,j)=6370*acos(temp);
end
end
d=d+d';L=102;w=50;dai=100;
%通过改良圈算法选取优良父代A
for k=1:w
c=randperm(100);
c1=[1,c+1,102];
flag=1;
while flag>0
flag=0;
for m=1:L-3
for n=m+2:L-1
if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))其中"yichuansuanfadata.txt"为各点之间的经纬坐标,数据如下:
53.7121 15.3046 51.1758 0.0322 46.3253 28.2753 30.3313 6.9348
56.5432 21.4188 10.8198 16.2529 22.7891 23.1045 10.1584 12.4819
20.1050 15.4562 1.9451 0.2057 26.4951 22.1221 31.4847 8.9640
26.2418 18.1760 44.0356 13.5401 28.9836 25.9879 38.4722 20.1731
28.2694 29.0011 32.1910 5.8699 36.4863 29.7284 0.9718 28.1477
8.9586 24.6635 16.5618 23.6143 10.5597 15.1178 50.2111 10.2944
8.1519 9.5325 22.1075 18.5569 0.1215 18.8726 48.2077 16.8889
31.9499 17.6309 0.7732 0.4656 47.4134 23.7783 41.8671 3.5667
43.5474 3.9061 53.3524 26.7256 30.8165 13.4595 27.7133 5.0706
23.9222 7.6306 51.9612 22.8511 12.7938 15.7307 4.9568 8.3669
21.5051 24.0909 15.2548 27.2111 6.2070 5.1442 49.2430 16.7044
17.1168 20.0354 34.1688 22.7571 9.4402 3.9200 11.5812 14.5677
52.1181 0.4088 9.5559 11.4219 24.4509 6.5634 26.7213 28.5667
37.5848 16.8474 35.6619 9.9333 24.4654 3.1644 0.7775 6.9576
14.4703 13.6368 19.8660 15.1224 3.1616 4.2428 18.5245 14.3598
58.6849 27.1485 39.5168 16.9371 56.5089 13.7090 52.5211 15.7957
38.4300 8.4648 51.8181 23.0159 8.9983 23.6440 50.1156 23.7816
13.7909 1.9510 34.0574 23.3960 23.0624 8.4319 19.9857 5.7902
40.8801 14.2978 58.8289 14.5229 18.6635 6.7436 52.8423 27.2880
39.9494 29.5114 47.5099 24.0664 10.1121 27.2662 28.7812 27.6659
8.0831 27.6705 9.1556 14.1304 53.7989 0.2199 33.6490 0.3980
1.3496 16.8359 49.9816 6.0828 19.3635 17.6622 36.9545 23.0265
15.7320 19.5697 11.5118 17.3884 44.0398 16.2635 39.7139 28.4203
6.9909 23.1804 38.3392 19.9950 24.6543 19.6057 36.9980 24.3992
4.1591 3.1853 40.1400 20.3030 23.9876 9.4030 41.1084 27.7149
其中奇数列为经度,偶数列为纬度
求解结果如下:
path =
1 至 19 列
1 17 3 36 43 93 46 59 100 98 51 80 50 15 42 20 30 74 83
20 至 38 列
87 92 2 45 67 82 48 72 14 27 10 84 18 40 79 77 31 97 85
39 至 57 列
65 64 11 76 69 94 70 19 63 62 26 29 34 66 90 86 8 39 78
58 至 76 列
47 23 58 81 22 71 37 7 68 25 49 28 57 88 61 16 91 41 4
77 至 95 列
73 13 24 32 12 53 33 75 5 60 9 38 44 54 55 96 89 6 56
96 至 102 列
21 99 101 52 95 35 102
long =
4.087894090467779e+04
时间已过 8.865015 秒。
>>