EKFmonocularSLAM论文阅读笔记(一)
论文全名是:1-Point RANSAC for EKF Filtering. Application to Real-Time Structure from Motion and Visual Odometry
论文下载链接,可以去这里下载!
EKFmonocularSLAM系统介绍,有一个开源网址,可供参考。
MATLAB源码可以参考官方提供的github。
中文标题:单点RANSAC的EKF滤波器,应用于实时运动视觉测距
摘要
随机样本一致性(RANSAC)已成为用于可能包含异常值的数据集进行稳定估计的最成功技术之一。 它的工作有两个部分:从随机最小数据子集构造模型假设,和评估支持全部数据的有效性。 在本文中,我们提出了一种RANSAC加扩展卡尔曼滤波器(EKF)的新型组合,它在RANSAC模型假设阶段使用来自EKF的可用先验概率信息。 这样可以将最小样本量减少到一个,从而大大节省计算量,而不会损失区分能力。 1点RANSAC被证明在联合兼容性分支和界限(JCBB)算法的精确度和计算成本方面均优于EKF框架内的杂散抑制的黄金标准技术。
在实验中使用两种视觉估计方案:首先,根据单眼序列(来自运动结构相机)的六个自由度运动估计。 在这里,提出了一种新的基于高分辨率图像的六种自由度视觉估计算法的基准测试方法,经过验证并用于展示1点RANSAC的优越性。 其次,我们结合单目视觉和轮测距(视觉测量)演示了长时期状态下机器人的轨迹估计。 在这里,与GPS的比较显示出与最先进的视觉测距方法有一样的精确度。
主要贡献:
(1)提出了一种新的基于高分辨率图像的六种自由度视觉估计算法的基准测试方法;
(2)结合单目视觉和轮测距(视觉测量)演示了长时期状态下机器人的轨迹估计。
一、随机抽样一致性算法(RANSAC)
详细介绍可以参考维基百科的翻译。
从传感器数据建立可靠的对应关系是机器人中大多数估算算法的核心。 对通信或数据关联的搜索通常基于比较测量数据中显著特征的局部描述符的第一阶段。 这种局部描述的模糊性导致在这个阶段可能出现不正确的对应关系。 鲁棒方法通过检查数据的一致性与假定要生成数据的全局模型的一致性来进行操作,并且将任何不适合的数据丢弃为虚假数据。 在具有鲁棒性的估计方法中,随机样本一致性(RANSAC)(Fischler和Bolles,1981)是最成功和最广泛使用的算法之一,尤其是在计算机视觉领域。
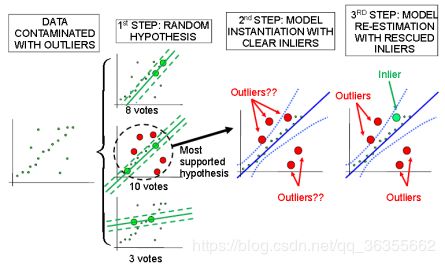
图1:简单2D平面直线估计示例的RANSAC步骤:首先,随机生成假设模型,从数据样本中随机选取两个点(两个点至少构成一条直线)。 选择支持度最高的一个,并对该假设进行数据投票。 在第二步中利用这些合理的局内点来估计模型参数。 最后,再次利用与最新模型一致的剩余数据点,并重新估计模型。
二、单点RANSAC扩展卡尔曼滤波算法
1、EKF预测和搜索单独兼容的匹配(第5-8行)
该算法从标准EKF预测开始:在步骤中估计第 k − 1 k-1 k−1步的状态向量 X k − 1 ∣ k − 1 X_{k-1|k-1} Xk−1∣k−1,建立一个多维高斯模型 X k − 1 ∣ k − 1 ∼ N ( X ^ k − 1 ∣ k − 1 , P k − 1 ∣ k − 1 ) X_{k-1|k-1}{\sim}N(\hat{X}_{k-1|k-1},P_{k-1|k-1}) Xk−1∣k−1∼N(X^k−1∣k−1,Pk−1∣k−1),然后通过已知的动态模型 f k f_k fk运行到第 k k k步:
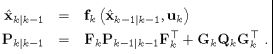
其中, u k u_k uk表示在步骤 k k k对系统的控制输入, F k F_k Fk是关于在步骤 k k k的状态向量 X k ∣ k − 1 X_{k|k-1} Xk∣k−1的 f k f_k fk的雅可比矩阵, Q k Q_k Qk是为动态模型假设的零均值高斯噪声的协方差, G k G_k Gk是该噪声相对于步骤 k k k中的状态向量 X k ∣ k − 1 X_{k|k-1} Xk∣k−1的雅可比行列式。
X k ∣ k − 1 X_{k|k-1} Xk∣k−1状态的预测概率分布可用于缓解搜索过程,通过测量模型 h i h_i hi在每次测量提供的高斯预测来传播这个预测状态:

其中, H i H_i Hi是关于状态向量 X k ∣ k − 1 X_{k|k-1} Xk∣k−1的测量 h i h_i hi的雅可比行列式, R i R_i Ri是每个单独测量假设的高斯噪声的协方差。 通过比较所选择的局部特征描述符,应当在由其预测的高斯 N ( h ^ i , S i ) N(\hat{h}_{i},S_i) N(h^i,Si)定义的99%概率区域内彻底搜索实际测量值 z i z_i zi。
主动搜索允许计算节省,并且还可以限制匹配与预测状态 X k ∣ k − 1 X_{k|k-1} Xk∣k−1单独兼容。 尽管如此,确保每个分离匹配 z i z_i zi的几何兼容性并不能保证整个集合的全局共识。 因此,仍然需要检查数据与全局模型的联合兼容性,以检查EKF更新之前的集合单独兼容匹配 z I C = ( z 1 . . . z i . . . z n ) T z^{IC} =(z_1 ... z_i ... z_n)^T zIC=(z1...zi...zn)T。
2、单点假设的产生和评估(第9-22行)
遵循RANSAC的原则,生成随机状态假设 x ^ i \hat{x}_i x^i,并通过对阈值内的测量进行计数来计算数据支持。 假定我们正在考虑预测测量高度相关的问题,使得通过一次匹配计算的每个假设减少了测量预测中的大部分相关性,其中内部不确定性接近测量噪声。 根据 x 2 x^2 x2检验确定阈值,意味着 a = 0.05 a = 0.05 a=0.05。
作为关于标准RANSAC的关键差异,不仅基于数据 z I C = ( z 1 . . . z i . . . z n ) T z^{IC} =(z_1 ... z_i ... z_n)^T zIC=(z1...zi...zn)T,而且还基于预测的状态生成随机假设。利用这一先验知识,我们可以减小从最小尺寸实例化模型参数所需的样本大小,以将模型的自由度确定为仅一个数据点。 终止标准随着样本大小呈指数增长,并且意味着假设数量的大幅减少。
假设涉及一个或多个异常值的假设得到较低的支持,为了确保在个假设数 n h y p n_{hyp} nhyp中至少有一个无假设假设已经用概率 p p p进行了测试,该概率 p p p可以从该公式计算出来:
n h y p = l o g ( 1 − p ) l o g ( 1 − ( 1 − ϵ ) m ) n_{hyp}=\frac{log(1-p)}{log(1-(1-\epsilon)^m)} nhyp=log(1−(1−ϵ)m)log(1−p)
其中 ϵ \epsilon ϵ是异常值比率, m m m是实例化模型所需的最小数据点数量。 通常的做法是在每次迭代时自适应地计算假设的数量,假设内部比率是由该迭代中的数据点总数设置的支持。
算法效率的另一个关键方面是每个假设 x i x_i xi生成只需要使用单个匹配 z i z_i zi的EKF状态更新。 不需要协方差更新,其状态大小是二次复杂的,每个假设的成本将会很低。 通过将更新后的状态投影到相机中来计算假设支持,与EKF算法中的其他阶段相比,这种支持也可以以非常低的成本执行。
3、部分更新与低创新Inlier(第23-24行)
数据点投票支持最多的假设 z l i − i n l i e r s z^{li-inliers} zli−inliers内点被指定为低创新内点。 假定它们是由真实模型生成的,因为它们与最受支持的假设距离很小。 其余的点可以是离群值,但也可以是内点,即使它们远离最受支持的假设。
在RANSAC假设生成步骤中,遥远的特征将产生一个高度准确的旋转1点假设,而转换将保持不准确的估计。 在这种情况下,其他遥远的地方会创新性低,并会投票支持这一假设。 但是,由于转换仍然不准确,即使是临时点,附近点也可能显示出高度创新。
因此,在确定了最受支持的假设和其他支持投票的点后,一些局内点集仍然不得不从高度创新集合中被挑选出来。在局部状态和协方差更新后,这些内点将仅使用可靠的低创新内点集来重新使用:
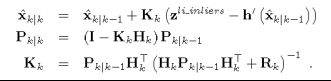
其中, H k H_k Hk表示测量方程 h h h的雅可比行列式,它将低创新的内点投影到传感器空间中。 R k R_k Rk是分配给传感器噪声的协方差。
4、部分更新与高创新Inliers(25-35行)
在使用低创新内点的部分更新之后,EKF预测中的大多数相关误差被校正并且协方差大大降低。 这种高度减少将被用于恢复高度创新的内部人员:因为相关性已经减弱,所以不需要对该集合进行共识来计算,并且个人兼容性将足以从异常值中舍弃内部人员。
通过在第一部分通过投影模型更新 x k ∣ k x_{k|k} xk∣k之后,针对每个匹配 z j z_j zj的每个高创新将会通过传播状态来计算单独的高斯预测 h j ∼ N ( h ^ j , S j ) h^j{\sim}N(\hat{h}^j,S^j) hj∼N(h^j,Sj)。 如果该匹配位于测量的预测高斯的99%概率区域内,则该匹配将被接受为内点。
在测试完所有高度创新的测量之后,将按照通常的EKF方程进行第二次部分更新,将所有点分类为内点 z h i − i n l i e r s z^{hi-inliers} zhi−inliers。
这里值得注意的是,拆分EKF更新对计算成本没有明显的影响。 如果 n n n是状态向量尺寸, m m m是测量向量尺寸,并且在状态远大于本地测量集合 n > > m n >> m n>>m的通常SLAM情况下,主要EKF成本是协方差更新 O ( m n 2 ) O(mn^2) O(mn2)。 如果更新被分成测量矢量大小 m 1 m_1 m1和 m 2 ( m = m 1 + m 2 ) m_2(m = m_1 + m_2) m2(m=m1+m2)两个步骤,则该协方差更新成本保持几乎相同。 其他一些小的成本也会增长,比如Jacobian计算必须进行两次。 但也有一些其他的减少,如 O ( m 3 ) O(m^3) O(m3)的测量协方差反演。 尽管如此,后两者的影响可以忽略不计,并且对于大多数EKF估计情况,成本由协方差更新支配,并且保持大致相同。

