吴恩达深度学习 —— 4.3 核对矩阵的维数
当实现深度神经网络的时候,常用的检验代码是否有错的方法是拿出一张纸,然后过一遍算法中矩阵的维数,下面会向大家展示具体怎么做。
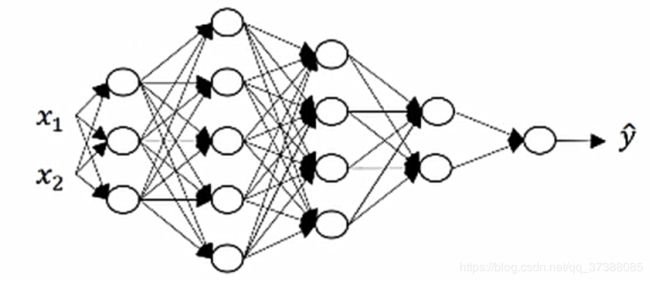
在上图的神经网络中,神经网络的层数为5层,总共有4个隐层和一个输出层,如果你想实现正向传播,第一步是 z [ 1 ] = w [ 1 ] x + b [ 1 ] z^{[1]}=w^{[1]}x+b^{[1]} z[1]=w[1]x+b[1],现在先忽略偏置项,只关注参数w。图中的第一隐藏层有三个隐藏单元,第一层隐藏层单元数是 n [ 1 ] n^{[1]} n[1],所以 n [ 1 ] = 3 n^{[1]}=3 n[1]=3,接下来 n [ 2 ] = 5 n^{[2]}=5 n[2]=5, n [ 3 ] = 4 n^{[3]}=4 n[3]=4, n [ 4 ] = 2 n^{[4]}=2 n[4]=2, n [ 5 ] = 1 n^{[5]}=1 n[5]=1。到目前为止我们只看到过只有一个输出单元的神经网络,在之后会学习有多个输出单元的神经网络,最后回到输入层, n [ 0 ] = 2 n^{[0]}=2 n[0]=2,然后我们看一下z,w和x的维数。z是第一个隐层的激活函数向量,z的维度为 ( 3 , 1 ) (3,1) (3,1),也就是一个三维的向量,也可以写成 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1)维向量;接着看输入特征x,x在这里有两个输入特征,所以x的维度为 ( 2 , 1 ) (2,1) (2,1),归纳起来x的维度就是 ( n [ 0 ] , 1 ) (n^{[0]},1) (n[0],1),所以我们需要 W [ 1 ] W^{[1]} W[1]这个矩阵就能够实现这样的结果,也就是当我们用 W [ 1 ] W^{[1]} W[1]乘于一个 ( n [ 0 ] , 1 ) (n^{[0]},1) (n[0],1)维向量时,我们会得到一个 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1)维向量。根据矩阵的乘法规则,可以知道 W [ 1 ] W^{[1]} W[1]的维度为 ( 3 , 2 ) (3,2) (3,2),也就是 ( n [ 1 ] , n [ 0 ] ) (n^{[1]},n^{[0]}) (n[1],n[0])维矩阵。
总结起来, W [ l ] W{[l]} W[l]的维度必须是 ( n [ l ] , n [ l − 1 ] ) (n^{[l]},n^{[l-1]}) (n[l],n[l−1])。现在再来看向量b的维度,在第一层中,b是一个 ( 3 , 1 ) (3,1) (3,1)向量,如果做向量加法,必须加上一个 ( 3 , 1 ) (3,1) (3,1)维度的矩阵,总结一下, b [ l ] b^{[l]} b[l]的维度为 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1)。
在实现反向传播的时候, d w dw dw的维度应该和 W W W的维度相同, d b db db的维度应该和 b b b的维度相同。我们还需要检查z,x和 a [ l ] a^{[l]} a[l]的维度,因为 z [ l ] z^{[l]} z[l]对应元素 g [ l ] ( a [ l ] ) g^{[l]}(a^{[l]}) g[l](a[l]),这里z和a的维度应该相同。
依照惯例,我们看看向量化的实现过程,这样就可以同时作用于多个样本。即使实现过程已经向量化了,w和dw,b和db的维度应该始终是一样的,但是Z,A以及X的维度会在向量化后发生变化。
在之前的情况中, z [ 1 ] = W [ 1 ] x + b [ 1 ] z^{[1]}=W^{[1]}x+b^{[1]} z[1]=W[1]x+b[1],这种情况下 z [ 1 ] , W [ 1 ] , x , b [ 1 ] z^{[1]},W^{[1]},x,b^{[1]} z[1],W[1],x,b[1]的维度分别是 ( n [ 1 ] , 1 ) , ( n [ 1 ] , n [ 0 ] ) , ( n [ 0 ] , 1 ) , ( n [ 1 ] , 1 ) (n^{[1]},1),(n^{[1]},n^{[0]}),(n^{[0]},1),(n^{[1]},1) (n[1],1),(n[1],n[0]),(n[0],1),(n[1],1)。
当一切向量化之后, Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]}=W^{[1]}X+b^{[1]} Z[1]=W[1]X+b[1], Z [ 1 ] Z^{[1]} Z[1]是从每一个单独的 z [ 1 ] z^{[1]} z[1]的值叠加得到的,所以 Z [ 1 ] Z^{[1]} Z[1]的维度不再是 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1),维度变为 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m),其中m是训练集大小, W [ 1 ] W^{[1]} W[1]的维度还是一样的,维度大小为 ( n [ 1 ] , n [ 0 ] ) (n^{[1]},n^{[0]}) (n[1],n[0]), X X X维度不再是 ( n [ 0 ] , 1 ) (n^{[0]},1) (n[0],1),而是把所有训练样本水平叠在一块,现在的维度为 ( n [ 0 ] , m ) (n^{[0]},m) (n[0],m)。当你把一个 ( n [ 1 ] , n [ 0 ] ) (n^{[1]},n^{[0]}) (n[1],n[0])矩阵乘于一个 ( n [ 0 ] , m ) (n^{[0]},m) (n[0],m)矩阵会得到一个 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m)矩阵, b [ 1 ] b^{[1]} b[1]的维度还是 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1),当b加上 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m)矩阵矩阵时,使用python的广播机制,b会 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m)矩阵,然后逐个元素相加。
向量化之后, z [ l ] z^{[l]} z[l]的维度和 a [ l ] a^{[l]} a[l]的维度从 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1)变为 ( n [ l ] , m ) (n^{[l]},m) (n[l],m)。还有个特别情况是当l等于0时,对应的 A [ 0 ] A^{[0]} A[0]也就等于输入的特征向量x,A^{[0]}的维度应该是 ( n [ 0 ] , m ) (n^{[0]},m) (n[0],m)。
如果你在实现反向传播的话,我们会发现在计算了 D Z [ l ] DZ{[l]} DZ[l]和 D A [ l ] DA^{[l]} DA[l]之后,会发现它们的维度跟 Z Z Z和 A A A是一样的,其维度为 ( n [ l ] , m ) (n^{[l]},m) (n[l],m)。