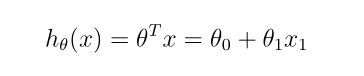机器学习---编程练习（一）：线性回归
机器学习—编程练习（一）：线性回归
文件列表：
ex1.m - Octave/MATLAB script that steps you through the exercise
ex1 multi.m - Octave/MATLAB script for the later parts of the exercise
ex1data1.txt - Dataset for linear regression with one variable
ex1data2.txt - Dataset for linear regression with multiple variables
submit.m - Submission script that sends your solutions to our servers
[*] warmUpExercise.m - Simple example function in Octave/MATLAB
[*] plotData.m - Function to display the dataset
[*] computeCost.m - Function to compute the cost of linear regression
[*] gradientDescent.m - Function to run gradient descent
[+] computeCostMulti.m - Cost function for multiple variables
[+] gradientDescentMulti.m - Gradient descent for multiple variables
[+] featureNormalize.m - Function to normalize features
[+] normalEqn.m - Function to compute the normal equations
[*]为需要完成的内容
[+]为可选择完成的内容
1 简单的Octave/Matlab函数
修改 warmUpExercise.m，使它返回一个5*5的单位矩阵
A = eye(5);
输出结果：
ans =
Diagonal Matrix
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
2 单一变量的线性回归
2.1 绘制数据
完成文件plotData.m绘制点图。将下列代码粘贴到plotData.m中
plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data rx表示绘制x形状的点
ylabel('Profit in $10,000s'); % Set the y?axis label
xlabel('Population of City in 10,000s'); % Set the x?axis label
如图：
2.2 梯度衰减
2.2.1 更新方程
最小化成本函数
梯度下降算法迭代更新函数
2.2.2 实现
练习中已经写好了,如下图所示：
2.2.3 计算成本函数 J(θ)
在 computeCost.m 中代码输入部分添加如下代码
h = X*theta; %计算hθ(x）
J = 1/(2*m) .* (h - y)'*(h - y);
%计算J，其中求和使用矩阵乘法完成。原理如下图所示
2.2.4 梯度下降
在gradientDescent.m中代码输入部分添加如下代码：
h = X*theta;
theta = theta - alpha / m .* X'*(h - y);
运行代码后将会出现下图
2.3 可视化
这部分不需要添加任何代码，为了将来便于复习，就将讲义上代码截下来了。
可视化结果
3 多变量的线性回归
3.1 特征归一化
完成文件featureNormalize.m ，求归一化。
归一化方法
求出每列数据的平均值和标准差。每列数据减去相应的平均值后除以标准差。
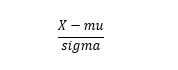
其中X是数据，mu是X的平均值，sigma是X的标准差
在featureNormalize.m 中输入下列代码
mu = mean(X);%求mu
sigma = std(X);
X_norm = (X - mu)./sigma;
上边代码不知道怎么回事，有时候能通过有时候不能通过。不行的话就用下面的
mu = mean(X);%求mu
sigma = std(X);
l_mu = size(X,2);
for i = 1:l_mu
X_norm(:,i) = (X(:,i) - mu(i))./sigma(i);
end
另外在ex1 multi.m第109行price = 0下面添加下列代码
predict = [1650,3];
predict = (predict - mu)./sigma;
price=[1,predict]*theta;
注意： 不能写成
price = [1,1650,3]*theta;
因为X中的数据是归一化后求得的theta，所以输入的price也需要归一化。
3.2 梯度下降
和单变量的代码一样，粘贴过去就行了
h = X*theta;
theta = theta - alpha / m .* X'*(h - y);
我的输出结果是这样的
3.2.1 改变学习率α
将迭代次数设置为50后，调整学习率，使他达到和之前迭代次数为400时一样的曲线。完成时如下图所示
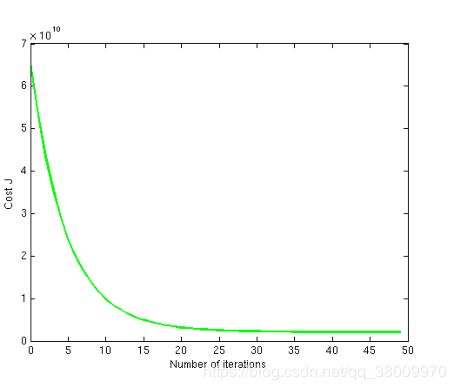
这个调整起来比较困难，我试了好多次都没调到这样的曲线。有兴趣的可以自己试一下。
从中可以得到的结论是：
如果学习率α过大，曲线将会下降的很快。这是学习率为1的情况。
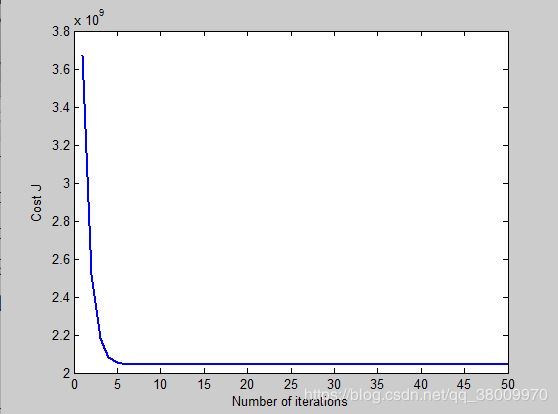
如果α过大，曲线下降的又会非常缓慢，还没找出最小损耗迭代就结束了。下图α为0.01
3.3 正规方程
这种方法不需要归一化，在 normalEqn.m 中添加下列代码直接运行ex1_multi就可以了。
如果没出错，将会和之前使用梯度衰减的方法产生相差不大的结果
theta = pinv(X'*X)*X'*y;
以及在ex1_multi中price = 0下添加
price = [1, 1650, 3] *theta;
我的结果： 