经典力学(动力学)——动量守恒定律与能量守恒定律
文章目录
- 质点和质点系的动量定理
- 冲量 质点的动量定理
- 冲量
- 质点的动量定理
- 质点系的动量定理
- 动量守恒定律 动能定律
- 动量守恒定律
- 动能定理
- 质点的动能定理
质点和质点系的动量定理
力的累积效应 { F ⃗ ( t ) 对 t 的 累 积 → I ⃗ , Δ p ⃗ F ⃗ 对 r ⃗ 累 积 → W , Δ E ⟹ \begin{cases} \vec{F}(t)对t的累积 \to \vec{I},\Delta\vec{p} \\ \vec{F}对\vec{r}累积 \to W,\Delta E\end{cases} \Longrightarrow {F(t)对t的累积→I,ΔpF对r累积→W,ΔE⟹ { 动 量 、 冲 量 、 动 量 定 理 、 动 量 守 恒 定 律 动 能 、 功 、 动 能 定 理 、 机 械 能 守 恒 定 律 \begin{cases} 动量、冲量、动量定理、动量守恒定律 \\ 动能、功、动能定理、机械能守恒定律 \end{cases} {动量、冲量、动量定理、动量守恒定律动能、功、动能定理、机械能守恒定律
冲量 质点的动量定理
冲量
动量(状态量): p ⃗ = m v ⃗ \vec{p}=m\vec{v} p=mv F ⃗ = d p ⃗ d t = d ( m v ⃗ ) d t ⇒ F ⃗ d t = d p ⃗ = d ( m v ⃗ ) ⇒ ∫ t 1 t 2 F ⃗ d t = p ⃗ 2 − p ⃗ 1 = m v ⃗ 2 − m v ⃗ 1 \vec{F}=\frac{d\vec{p}}{dt}=\frac{d(m\vec{v})}{dt} \Rightarrow \vec{F}dt=d\vec{p}=d(m\vec{v})\Rightarrow \int_{t_1}^{t_2}\vec{F}dt=\vec{p}_2-\vec{p}_1=m\vec{v}_2-m\vec{v}_1 F=dtdp=dtd(mv)⇒Fdt=dp=d(mv)⇒∫t1t2Fdt=p2−p1=mv2−mv1
冲量定义(过程量): I ⃗ = ∫ t 1 t 2 F ⃗ d t \vec{I}=\int_{t_1}^{t_2}\vec{F}dt I=∫t1t2Fdt
质点的动量定理
微分形式: F ⃗ d t = d p ⃗ = d ( m v ⃗ ) \vec{F}dt=d\vec{p}=d(m\vec{v}) Fdt=dp=d(mv)
积分形式: I ⃗ = ∫ t 1 t 2 F ⃗ d t = p ⃗ 2 − p ⃗ 1 = m v ⃗ 2 − m v ⃗ 1 \vec{I}=\int_{t_1}^{t_2}\vec{F}dt=\vec{p}_2-\vec{p}_1=m\vec{v}_2-m\vec{v}_1 I=∫t1t2Fdt=p2−p1=mv2−mv1
动 量 定 理 \red{动量定理} 动量定理:在给定时间间隔内,外力作用在质点上的冲量,等于质点在此时间内动量的增量。
以上两种形式也可用分量表示,某方向收到冲量,该方向的动量就增加。
质点系的动量定理

对两质点分别用质点动量定理:
{ ∫ t 1 t 2 ( F ⃗ 1 + F ⃗ 12 ) d t = m 1 v ⃗ 1 − m 1 v ⃗ 10 ∫ t 1 t 2 ( F ⃗ 2 + F ⃗ 21 ) d t = m 2 v ⃗ 2 − m 2 v ⃗ 20 \begin{cases}\int_{t_1}^{t_2}(\vec{F}_1+\vec{F}_{12})dt=m_1\vec{v}_1-m_1\vec{v}_{10}\\ \int_{t_1}^{t_2}(\vec{F}_2+\vec{F}_{21})dt=m_2\vec{v}_2-m_2\vec{v}_{20} \end{cases} {∫t1t2(F1+F12)dt=m1v1−m1v10∫t1t2(F2+F21)dt=m2v2−m2v20
因为内力和 F ⃗ 12 + F ⃗ 21 = 0 \vec{F}_{12}+\vec{F}_{21}=0 F12+F21=0,所以两式相加后:
∫ t 1 t 2 ( F ⃗ 1 + F ⃗ 2 ) d t = ( m 1 v ⃗ 1 + m 2 v ⃗ 2 ) − ( m 1 v ⃗ 10 + m 2 v ⃗ 20 ) \int_{t_1}^{t_2}(\vec{F}_1+\vec{F}_2)dt=(m_1\vec{v}_1+m_2\vec{v}_2)-(m_1\vec{v}_{10}+m_2\vec{v}_{20}) ∫t1t2(F1+F2)dt=(m1v1+m2v2)−(m1v10+m2v20)
即:
I ⃗ = ∫ t 1 t 2 F ⃗ e x d t = ∑ i = 1 n m i v ⃗ i − ∑ i = 1 n m i v ⃗ i 0 = p ⃗ − p ⃗ 0 \vec{I}=\int_{t_1}^{t_2}\vec{F}^{ex}dt=\sum_{i=1}^{n}m_i\vec{v}_i-\sum_{i=1}^{n}m_i\vec{v}_{i0}=\vec{p}-\vec{p}_0 I=∫t1t2Fexdt=i=1∑nmivi−i=1∑nmivi0=p−p0
质 点 系 动 量 定 理 : \red{质点系动量定理:} 质点系动量定理:作用于系统的合外力的冲量等于系统动量的增量。
注意:要区分内力和外力,内力仅能改变系统内某个物体的动量,但不能改变系统的总动量。
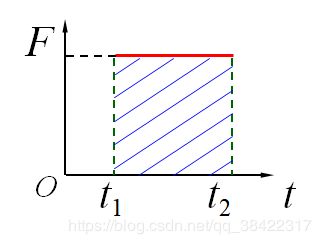
(1) F F F为恒力, I ⃗ = F ⃗ Δ t \vec{I}=\vec{F}\Delta t I=FΔt

(2) F F F为变力, I ⃗ = ∫ t 1 t 2 F ⃗ d t = F ⃗ ‾ ( t 2 − t 1 ) \vec{I}=\int_{t_1}^{t_2}\vec{F}dt= \overline {\vec{F}}(t_2-t_1) I=∫t1t2Fdt=F(t2−t1)( 平 均 冲 力 \red{平均冲力} 平均冲力)
动量定理经常应用于碰撞问题

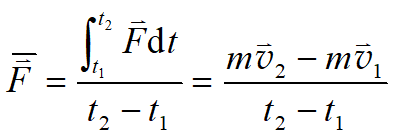
在 Δ p ⃗ 一 定 时 , Δ t 越 小 , F ⃗ ‾ 越 大 \Delta \vec{p}一定时,\Delta t越小, \overline {\vec{F}}越大 Δp一定时,Δt越小,F越大
动量守恒定律 动能定律
动量守恒定律
质点系动量定理:
I ⃗ = ∫ t 1 t 2 ∑ i F ⃗ i e x = ∑ i p ⃗ i − ∑ i p ⃗ i 0 \vec{I}=\int_{t_1}^{t_2}\sum_{i}^{}\vec{F}_i^{ex}=\sum_{i}^{}\vec{p}_i-\sum_{i}^{}\vec{p}_{i0} I=∫t1t2i∑Fiex=i∑pi−i∑pi0若质点系所受合外力为0:
F ⃗ e x = ∑ i F ⃗ i e x = 0 \vec{F}^{ex}=\sum_{i}^{}\vec{F}_i^{ex}=0 Fex=i∑Fiex=0则系统的 总 动 量 \blue{总动量} 总动量不变———— 动 量 守 恒 定 律 \red{动量守恒定律} 动量守恒定律
动能定理
力的空间累积效应:
做 功 : \red{做功:} 做功:物体在力 F ⃗ \vec{F} F作用下移动 Δ r ⃗ ⇒ \Delta \vec{r} \Rightarrow Δr⇒做功W
做功分为恒力下做功和变力下做功:
恒力作用下的功:

W = F c o s θ ⋅ ∣ Δ t ⃗ ∣ = F ⃗ ⋅ Δ r ⃗ W=Fcos\theta \cdot |\Delta \vec{t}|=\vec{F}\cdot \Delta \vec{r} W=Fcosθ⋅∣Δt∣=F⋅Δr
变力作用下的功:
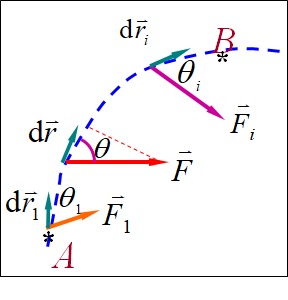
d W = F ⃗ ⋅ d r ⃗ = F c o s θ ⋅ ∣ d r ⃗ ∣ = F c o s θ ⋅ d s dW=\vec{F}\cdot\ d\vec{r}=Fcos\theta \cdot|d\vec{r}|=Fcos\theta \cdot ds dW=F⋅ dr=Fcosθ⋅∣dr∣=Fcosθ⋅ds ⇒ W = ∫ A B F ⃗ ⋅ d r ⃗ = ∫ A B F c o s θ ⋅ d s \Rightarrow W=\int_{A}^{B}\vec{F}\cdot\ d\vec{r}=\int_{A}^{B}Fcos\theta \cdot ds ⇒W=∫ABF⋅ dr=∫ABFcosθ⋅ds
其中 θ \theta θ为力与相对应位移的夹角。
(1)关于功的正负: { 0 o < θ < 9 0 o , d W > 0 9 0 o < θ < 18 0 o , d W < 0 θ = 9 0 o , F ⃗ ⊥ r ⃗ , d W = 0 \begin{cases} 0^o<\theta <90^o ,dW>0 \\ 90^o<\theta <180^o ,dW<0 \\ \theta =90^o ,\vec{F} \perp \vec{r},dW=0 \end{cases} ⎩⎪⎨⎪⎧0o<θ<90o,dW>090o<θ<180o,dW<0θ=90o,F⊥r,dW=0
(2)做功的直观图示:

W = ∫ s 1 s 2 F c o s θ d s W=\int_{s_1}^{s_2}Fcos\theta ds W=∫s1s2Fcosθds
(3)功是一个过程量,与路径有关。
(4)合力的功,等于各分力的功的代数和。
| 功的单位(焦耳) | 1 J = 1 N ⋅ m 1J=1N \cdot m 1J=1N⋅m |
|---|---|
| 平均功率 | P ‾ = Δ W Δ t \overline{P}=\frac{\Delta W}{\Delta t} P=ΔtΔW |
| 瞬时功率 | P = lim Δ t → 0 Δ W Δ t = d W d t = F ⃗ ⋅ v ⃗ = F v c o s θ P=\lim_{\Delta t\to 0}\frac{\Delta W}{\Delta t}=\frac{dW}{dt}=\vec{F}\cdot \vec{v}=Fvcos\theta P=Δt→0limΔtΔW=dtdW=F⋅v=Fvcosθ |
| 功率单位(瓦特) | 1 W = 1 J . s − 1 , 1 k W = 1 0 3 W 1W = 1 J.s^{-1} ,1kW=10^3W 1W=1J.s−1,1kW=103W |
质点的动能定理
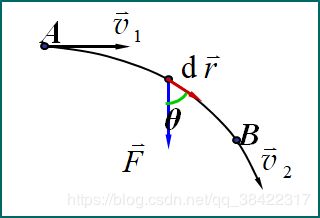
W = ∫ F ⃗ ⋅ d r ⃗ = ∫ F t ⋅ ∣ d r ⃗ ∣ = ∫ F t d s = ∫ m d v d t d s = ∫ v 1 v 2 m v d v = 1 2 m v 2 2 − 1 2 m v 1 2 = E k 2 − E k 1 W=\int \vec{F} \cdot d\vec{r}=\int F_t\cdot |d\vec{r}|=\int F_tds=\int m\frac{dv}{dt}ds=\int_{v_1}^{v_2}mvdv=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=E_{k2}-E_{k1} W=∫F⋅dr=∫Ft⋅∣dr∣=∫Ftds=∫mdtdvds=∫v1v2mvdv=21mv22−21mv12=Ek2−Ek1
合外力对质点所做的功,等于质点动能的增量—— 质 点 动 能 定 理 \red{质点动能定理} 质点动能定理
T i p s : \red{Tips:} Tips:功是 过 程 量 \blue{过程量} 过程量,动能是 状 态 量 \blue{状态量} 状态量
功和动能依赖于惯性系的选取,但对不同惯性系动能定理形式相同。