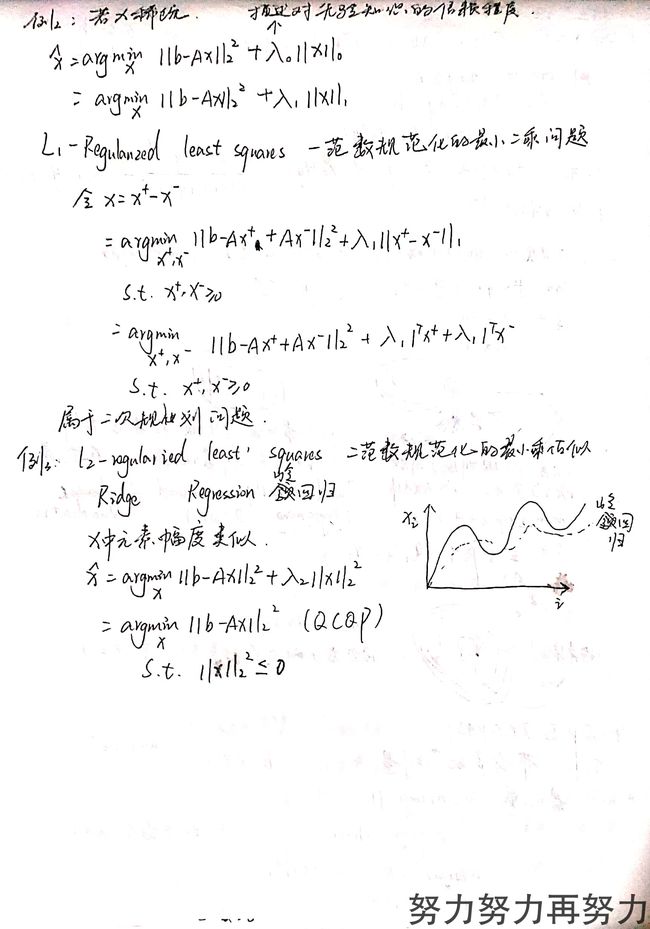
凸优化学习-(十六)几种典型的凸优化问题
凸优化学习
几种典型的凸优化问题。
学习笔记
一、线性规划
形如:
min C T x + d s.t. G x − h ≤ 0 A x − b = 0 \begin{aligned} \min&& \textbf C^Tx+d&\\ \text{s.t.}&&\textbf G x-h&\le0\\ &&\textbf A x-b&=0\\ \end{aligned} mins.t.CTx+dGx−hAx−b≤0=0
其中线性规划的约束本质是个多面体。
线性规划中的 ( y − x ∗ ) ∇ f ( x ∗ ) ≥ 0 (y-x^*)\nabla f(x^*)\ge0 (y−x∗)∇f(x∗)≥0:
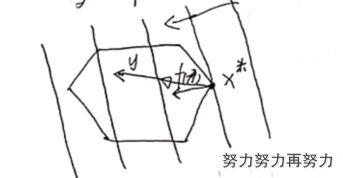
其中很明显内积大于零,两者夹角小于90度。
线性规划的变形
1、松弛变量
形如:
min C T x + d s.t. G x − h + s = 0 A x − b = 0 s ≥ 0 \begin{aligned} \min&& \textbf C^Tx+d&\\ \text{s.t.}&&\textbf G x-h+s&=0\\ &&\textbf A x-b&=0\\ && s&\ge0 \end{aligned} mins.t.CTx+dGx−h+sAx−bs=0=0≥0
其中 G x − h = − s , s ≥ 0 ⇒ G x − h ≤ 0 , s \textbf G x-h=-s,s\ge0\Rightarrow G x-h\le0,s Gx−h=−s,s≥0⇒Gx−h≤0,s称为松弛变量。
2、最优解正负分离
形如:
min C T X X = [ x ∗ , x + , x − ] s.t. A x − b = 0 X ≥ 0 \begin{aligned} \min&& \textbf C^TX&\qquad \textbf X=[x^*,x^+,x^-]\\ \text{s.t.}&&\textbf Ax-b&=0\\ &&\textbf X&\ge0\\ \end{aligned} mins.t.CTXAx−bXX=[x∗,x+,x−]=0≥0
其中 x + , x − x^+,x^- x+,x−指 x x x中正或负的元素, x ∗ = x + − x − x^*=x^+-x^- x∗=x+−x−
线性规划的一些例子
1、食谱问题
选择食谱,使食谱的 n n n种营养元素分别不小于 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm,有 n n n种食物,单位食物营养为 a i j , ⋯ , a n j a_{ij},\cdots,a_{nj} aij,⋯,anj,单位食物价格 c j c_j cj,找出总价最小的食谱。
**解:**设食物量分别为 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn,问题可描述为:
min ∑ j = 1 n c j x j s.t. ∑ j = 1 n a i j x j ≥ b i i = 1 ⋯ m x j ≥ 0 j = 1 ⋯ n \begin{aligned} \min&& \sum_{j=1}^nc_jx_j\\ \text{s.t.}&&\sum_{j=1}^na_{ij}x_j&\ge b_i\qquad i=1\cdots m\\ &&x_j&\ge0\qquad j=1\cdots n\\ \end{aligned} mins.t.j=1∑ncjxjj=1∑naijxjxj≥bii=1⋯m≥0j=1⋯n
2、线性分数规划 Linear fractional programming \text{Linear fractional programming} Linear fractional programming
形如:
min c T x + d e T x + f s.t. G x − h ≤ 0 A x − b = 0 \begin{aligned} \min&& \frac{c^Tx+d}{e^Tx+f}&\\ \text{s.t.}&&\textbf G x-h&\le0\\ &&\textbf A x-b&=0\\ \end{aligned} mins.t.eTx+fcTx+dGx−hAx−b≤0=0
等价于:
min c T y + d z s.t. G x − h z ≤ 0 A y − b z = 0 \begin{aligned} \min&& c^Ty+dz&\\ \text{s.t.}&&\textbf G x-hz&\le0\\ &&\textbf A y-bz&=0\\ \end{aligned} mins.t.cTy+dzGx−hzAy−bz≤0=0
其中 y = x e T x + f , z = 1 e T x + f y=\frac{x}{e^Tx+f},z=\frac{1}{e^Tx+f} y=eTx+fx,z=eTx+f1
二、二次规划(QP问题)
形如:
min 1 2 x T P x + q T x + r P ∈ S + n s.t. G x − h ≤ 0 A x − b = 0 \begin{aligned} \min&& \frac 1 2x^T\textbf Px+q^Tx+r&\qquad\textbf P\in\textbf S_+^n\\ \text{s.t.}&&\textbf G x-h&\le0\\ &&\textbf A x-b&=0\\ \end{aligned} mins.t.21xTPx+qTx+rGx−hAx−bP∈S+n≤0=0
二次规划中的 ( y − x ∗ ) ∇ f ( x ∗ ) ≥ 0 (y-x^*)\nabla f(x^*)\ge0 (y−x∗)∇f(x∗)≥0:
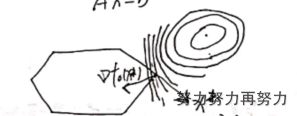

三、二次约束的二次规划(Quadratically constrained Quadratic programming)
并不是二次规划的子问题。
形如:
min 1 2 x T P x + q T x + r P ∈ S + n s.t. 1 2 x T P i x + q i x + r ≤ 0 A x − b ≤ 0 \begin{aligned} \min&& \frac 1 2x^T\textbf Px+q^Tx+r&\qquad\textbf P\in\textbf S_+^n\\ \text{s.t.}&& \frac 1 2x^T\textbf P_ix+q_ix+r&\le0\\ &&\textbf A x-b&\le0\\ \end{aligned} mins.t.21xTPx+qTx+r21xTPix+qix+rAx−bP∈S+n≤0≤0
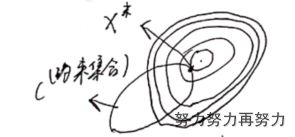
明显比二次规划更复杂,因为最优解不在顶点上(没有顶点)。
个人思考
到现在为止学的凸问题的解法大同小异,就不过多说明了。