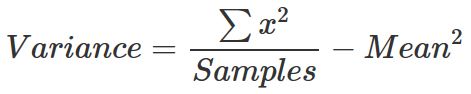Chango的数学Shader世界（十五）油画Shader-技术分析，教程纠错

目的：

实现油画后期Shader，探究教程中技术细节，指出错误。

参考：

搜索ue4 paint filter。

UE4.21后整合自定义usf

观察：

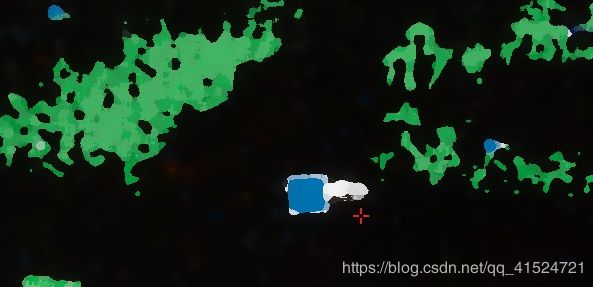
油画的特点：成块的色块，但又保持清晰的边缘。

分析：

1.先来看一种比较“差”的油画实现

先看下外网上的一种简单油画算法。

注意这位大师是怎么处理木头纹理的。还有后边黑方块上的纹理是多么残缺。

有些边缘没有得到保留。（处理草倒是很好看，类比The Witness中的树叶处理）

章鱼脚的细节变得非常非常抽象

奇怪的蓝色（r=0,g=1,b=1）出现了。具体原因稍加思考就知，源码在下。

基本思路：

1.在以当前像素为中心的n*n核中，基于每个像素点对应的intensity（r+g+b），
对所有像素进行分级归纳（intensity=0,1,2,3....）

2.对于频次最高的intensity级，计算桶中所有像素平均值，作为结果

int TexIndex = 14;

 int intensityCount[10];
 float avgR[10];
 float avgG[10];
 float avgB[10];
 

 for (int iLevel = 0; iLevel < 10; iLevel++){
     intensityCount[iLevel] = 0;
     avgR[iLevel] = 0.0;
     avgG[iLevel] = 0.0;
     avgB[iLevel] = 0.0;
  }


 //COUNT INTENSITIES
 uv *= 0.5;
 for (int i = 0; i < radius; ++i)
 {
     int offsetI = -1 *(radius / 2) + i;
     float v = uv.y + offsetI * invSize.y;
     int temp = i * radius;
     for (int j = 0; j < radius; ++j)
    {
         int offsetJ = -(radius / 2) + j;
         float u = uv.x + offsetJ * invSize.x;
         float2 uvShifted = uv + float2(u, v);
         float3 tex = SceneTextureLookup(uvShifted, TexIndex, false);

        float currentIntensity = ((tex.r + tex.g + tex.b) / 3 * 10);
        intensityCount[currentIntensity]++;
        avgR[currentIntensity] += tex.r;
        avgG[currentIntensity] += tex.g;
        avgB[currentIntensity] += tex.b;
    }
  }


 float maxIntensity = 0;
 int maxIndex = 0;

 //FIND CORRECT MOST COMMON INTENSITY LEVEL
 for(int cLevel = 0; cLevel < 10; cLevel++){
     if(intensityCount[cLevel] > maxIntensity){
         maxIntensity = intensityCount[cLevel];
         maxIndex = cLevel;
     }
  }

 float newR = avgR[maxIndex] / maxIntensity;
 float newG = avgG[maxIndex] / maxIntensity;
 float newB = avgB[maxIndex] / maxIntensity;

 float4 res = float4(newR, newG, newB, 1.0);

 return res;

2.简述方向Kuwahara算法思路

上面的油画算法，优点在于注意到了色块化画面的要领在于寻找邻域的最普遍的颜色并取平均。缺点在于边缘也因此模糊。因此，所有的色块都像是一滩水，从形状上来说，更像是水彩而不是油画的笔触。

Kuwahara我也不介绍了，网上都有。它的4部分选择性导致了即使在边缘处，也能选择到界内的色块，因此不会模糊边缘。方向Kuwahara是在此基础上将卷积核沿着边缘旋转，减少了斜边的田子形色块。具体演示原教程都有。

教程写得很好，我只在此简单总结一下思路（建议先看下面我的纠错，然后阅读原教程）

1.通过Sobel算法获得梯度向量与u轴的夹角
2.使用Kuwahara，只不过在采样周围像素的时候，将offset向量乘以旋转矩阵，这样整个卷积核就和边缘平行
3.返回Kuwahara的4部分当中方差最小部分的像素均值

Global.usf （提供全局函数）

    return 1;
}

float4 GetKernelMeanAndVariance(float2 UV, float4 Range, float2x2 RotationMatrix)
{
    float2 TexelSize = View.BufferSizeAndInvSize.zw;
    float3 Mean = float3(0, 0, 0);
    float3 Variance = float3(0, 0, 0);
    float Samples = 0;
    
    for (int x = Range.x; x <= Range.y; x++)
    {
        for (int y = Range.z; y <= Range.w; y++)
        {
            float2 Offset = mul(float2(x, y) * TexelSize, RotationMatrix);
            float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb;
            Mean += PixelColor;
            Variance += PixelColor * PixelColor;
            Samples++;
        }
    }
    
    Mean /= Samples;
    Variance = Variance / Samples - Mean * Mean;
    float TotalVariance = Variance.r + Variance.g + Variance.b;
    return float4(Mean.r, Mean.g, Mean.b, TotalVariance);
}

float GetPixelAngle(float2 UV)
{
    float2 TexelSize = View.BufferSizeAndInvSize.zw;
    float GradientX = 0;
    float GradientY = 0;
    float SobelX[9] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
    float SobelY[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
    int i = 0;
    
    for (int x = -1; x <= 1; x++)
    {
        for (int y = -1; y <= 1; y++)
        {
            // 1
            float2 Offset = float2(x, y) * TexelSize;
            float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb;
            float PixelValue = dot(PixelColor, float3(0.3,0.59,0.11));
            
            // 2
            GradientX += PixelValue * SobelX[i];
            GradientY += PixelValue * SobelY[i];
            i++;
        }
    }
    
    return atan(GradientY / GradientX);

Kuwahara.usf （算法主体）

float2 UV = GetDefaultSceneTextureUV(Parameters, 14);
float4 MeanAndVariance[4];
float4 Range;
float Angle = GetPixelAngle(UV);
float2x2 RotationMatrix = float2x2(cos(Angle), -sin(Angle), sin(Angle), cos(Angle));

Range = float4(-XRadius, 0, -YRadius, 0);
MeanAndVariance[0] = GetKernelMeanAndVariance(UV, Range, RotationMatrix);

Range = float4(0, XRadius, -YRadius, 0);
MeanAndVariance[1] = GetKernelMeanAndVariance(UV, Range, RotationMatrix);

Range = float4(-XRadius, 0, 0, YRadius);
MeanAndVariance[2] = GetKernelMeanAndVariance(UV, Range, RotationMatrix);

Range = float4(0, XRadius, 0, YRadius);
MeanAndVariance[3] = GetKernelMeanAndVariance(UV, Range, RotationMatrix);

// 1
float3 FinalColor = MeanAndVariance[0].rgb;
float MinimumVariance = MeanAndVariance[0].a;

// 2
for (int i = 1; i < 4; i++)
{
    if (MeanAndVariance[i].a < MinimumVariance)
    {
        FinalColor = MeanAndVariance[i].rgb;
        MinimumVariance = MeanAndVariance[i].a;
    }
}

return FinalColor;

3.纠错之Sobel梯度

原教程中，有这样一段：

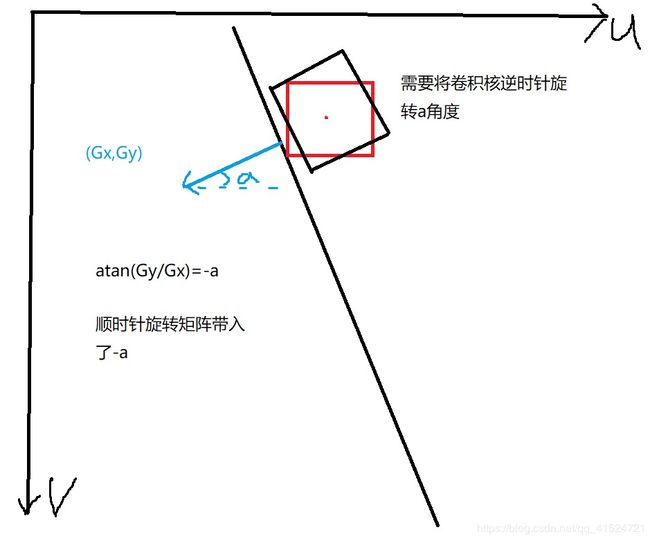
我们都知道Sobel算出来的（Gx,Gy），是梯度方向。怎么到你这，就成了边缘方向了？

要知道，沿着梯度方向函数变化最大，而且是正的。梯度方向垂直于等值线。

那么原文错在哪了？uv方向的v方向错了，在ue4 hlsl中v是向下的。所以(Gx,Gy)是这样的：

梯度方向变化最大，切垂直于等值线，对了。

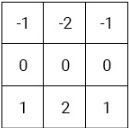
有兴趣可看之前转载了Sobel数学原理。并且你看它原文使用的垂直方向卷积核：

若上0下1，卷积为正，梯度向下，本身就已经告诉你v轴向下了。

所以，原文的角度就理解错了，角度是梯度与u轴的带正负的夹角。

那它角度理解错了，卷积核还能转正确？没错，能，接下来我就详细解释。

4.线性变换矩阵，旋转矩阵

对于矩阵的一个重要理解，3B1B的动画展现得十分清晰，就是线性变换矩阵的

可以看成对标准坐标系的拉扯，

将横，纵轴拉扯为。

以一个矩阵为例，就是将整个2D空间横轴放大3倍，纵轴放大4倍，单位方块面积变为原来的12倍。

这个”拉扯理解“，也使用于旋转矩阵。

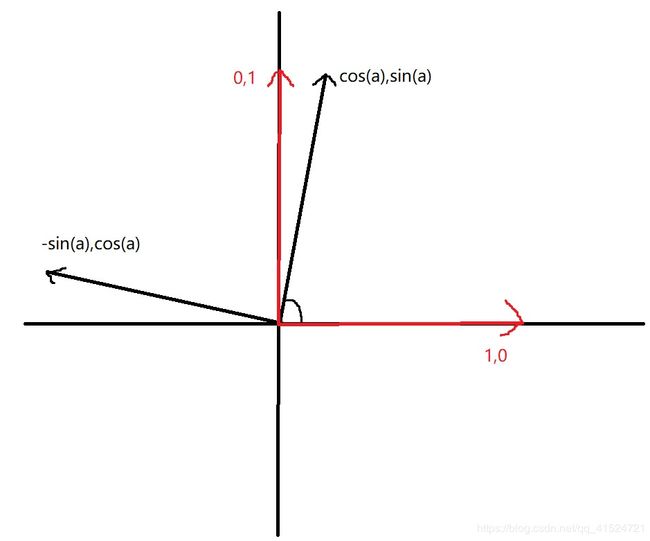
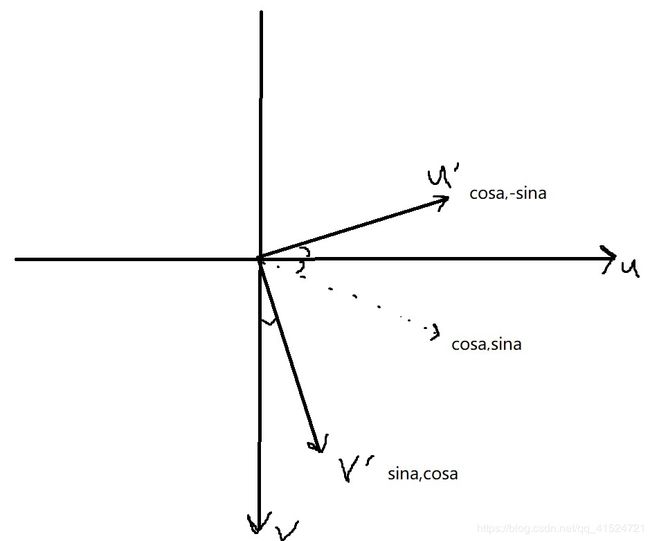
在传统数学的x,y屏幕内（x向右y向上），如果有旋转矩阵，你不妨画出向量，想象一下是怎么拉成成对应向量的。

没错，就是逆时针旋转正a角度（或者说，从x到y旋转）

那么问题来了，我们可以在源码中看见，即使在“方向不同”的uv系中，原文仍然使用了同样的矩阵用作旋转。那这个矩阵在uv系中是怎样旋转的呢？

顺时针旋转正a角度（或者说，从u到v旋转）

接下来我举个例子，证明原文是怎样歪打正着正确旋转了卷积核。也许写算法的本人知道这一点，但教程作者从角度开始就理解不对。

此时已经可以看出来了，顺时针旋转-a就是逆时针旋转了a。

具体来讲，带入-a的旋转矩阵此时为

这样，卷积核终于被旋转到了沿着边缘的方向，代码中是offset向量被旋转。

4.1矩阵扩展

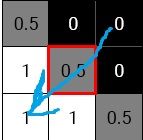
已知矩阵4点坐标怎样判断另一点是否在矩阵内？

1.将原点与一顶点对齐，得平移矩阵T
2.计算两边向量[a,c]和[b,d]，组成矩阵RS（旋转与缩放），计算RS逆矩阵Inv
3.将判定点v进行计算，v2=Inv*T*v，再判断v2两坐标是否在[0,1]内

应该不会有计算冗余。

5.简单的优化

俄文版对比英文版，多了方差公式的介绍，这里也提一下。

普通的方差公式大家初高中都能牢记了。代码中的计算方差，也是很常见方差计算。但你如果和我一样菜就对它不太熟悉。

至于为啥要这样，当然是计算复杂度啦。

如果按传统方差计算，在已算Mean的情况下，需要n个减，n个方，n个加，1个除

这样算，需要n个方，n个加，1个除，1个方，1个减

多了一个方，少了n-1个减。（还不考虑临时变量这些）

关于这种表达式算度之类的数学分支，不知道是什么...怎样定义哪种合并更好？...

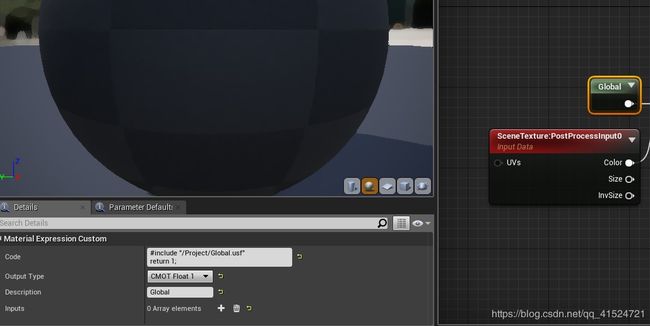
6.UE4的自定义usf

就本例来看，我认为单独拆usf文件出来并无必要,materialFunctionCall够用了。当然，可能有些人就是喜爱这种编写方式。

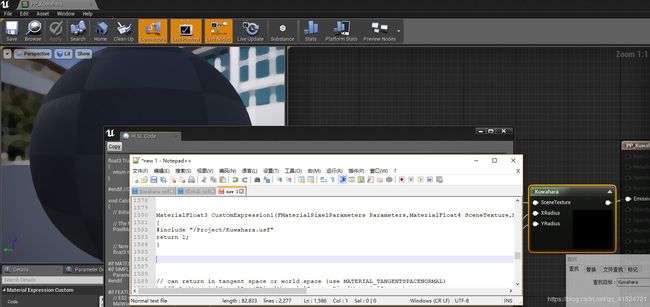
首先，你知道Custom节点里可以写HLSL代码，并且是写在一个函数里的。

通过打开视图里的HLSL Code，再蛋疼的将他复制出来，再搜索关键词（比如你的参数名），就能找到你的HLSL代码对应的函数位置。

从图中你可以看出引用路径之间为/Project/xxx.usf。

但你的项目路径可没有Project这个文件夹，这是引擎内部资源管理文件路径。

你得想办法把你的usf添加进去。

在UE4.21之前，直接在项目文件夹下新建Shader文件夹，往里头加就行了。

在UE4.21之后，得手动在C++项目引入。教程在最开头参考里给了。

你可能注意到之前的代码，Global.usf的结构是这样的：

return 1;
}
...

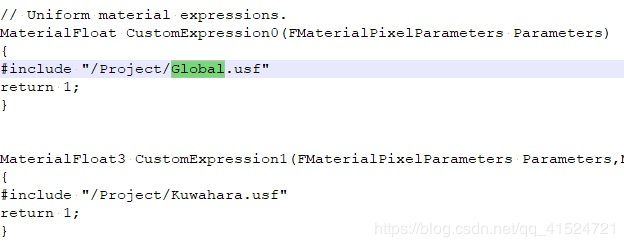
return xxx;

很诡异，因为在引擎中引入此文件后：

生成代码是这样的：

编译之后，它会很nc地将整个usf内容替换进函数里

MaterialFloat CustomExpression0(....)
{
nc替换
return 1;
}

变成

MaterialFloat CustomExpression0(....)
{
//Global.usf中的内容开始
return 1;
}
...

SomeFunc(...)
{
...
return xxx;
//Global.usf中的内容结束
return 1;
}

那么，我们地Global.usf这样写，就将自己的函数放置在了Custom函数外，成了可以跨Custom节点调用地函数。

虽然讨巧，但引擎中Custom节点include以后，return 1;仍然要写，不符逻辑，很nc。

 

与简单油画算法的优势对比

1.木板的笔触

2.黑色方块纹理的完整性，因为Kuwahara保留边缘信息

相对清晰的边缘

章鱼脚分得更细

没有诡异蓝边了。

 

结语

你觉得秦九韶这样的人怎么样？