Dijkstra(迪杰斯特拉算法)的实现-------------------------C,C++,Matlab实现
Dijkstra
一.算法背景
Dijkstra 算法(中文名:迪杰斯特拉算法)是由荷兰计算机科学家 Edsger Wybe Dijkstra 提出。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说,如果图中的顶点表示城市,而边上的权重表示城市间开车行经的距离,该算法可以用来找到两个城市之间的最短路径。
二.算法描述
算法思想:
设G=(V,E)是一个带权有向图,把图中顶点集合V分为两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),
第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径的的递增次序依次把第二组中的顶点加入S中。在加入的过程中,总保持从源点v到S中各个顶点的最短路径长度不大于从源点v到U中任何路径的长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前路径的最短长度。
算法步骤
a.初始时,只包括源点,即S = {v},v的距离为0。U包含除v以外的其他顶点,即:U ={其余顶点},若v与U中顶点u有边,则(u,v)为正常权值,若u不是v的出边邻接点,则(u,v)权值 ∞;
b..从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画
三:时间复杂度
设图的边数为 m,顶点数为 n。
Dijkstra 算法最简单的实现方法是用一个数组来存储所有顶点的dis[] 时间复杂度为O(n^2)
对于边数少于n^{2}的稀疏图来说,我们可以用邻接表来更有效的实现该算法。同时需要将一个二叉堆或者斐波纳契堆用作优先队列来查找最小的顶点(Extract-Min)。当用到二叉堆的时候,算法所需的时间为{\displaystyle O((m+n)logn)},斐波纳契堆能稍微提高一些性能,让算法运行时间达到{\displaystyle O(m+nlogn)}。然而,使用斐波纳契堆进行编程,常常会由于算法常数过大而导致速度没有显著提高。
四.算法缺点
算法限制要求:无负权值
无法求出任意两点路径(求任意两点 为 弗洛伊德算法(floyd))
五.算法实例
给出一个无向图
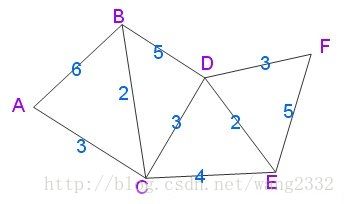
用Dijkstra算法找出以A为起点的单源最短路径步骤如下:
六.代码实现
以下为 C,C++,Matlab 语言的代码
C语言
例题:sdut 3562 Proxy (迪杰斯特拉+反向建树)
#include
C语言_优化(队列)
例题:sdut 3562 Proxy (迪杰斯特拉+反向建树)
#include
if(dis[s[c%2][j]]
{ min=dis[s[c%2][j]];
if(k!=-1)s[(c+1)%2][d++]=k;
k=s[c%2][j];
}
else s[(c+1)%2][d++]=s[c%2][j];
if(q==d)break;//寻找无改变 则未联通
for(j=0;j
if(dis[s[(c+1)%2][j]]>(dis[k]+mp[k][s[(c+1)%2][j]]))dis[s[(c+1)%2][j]]=dis[k]+mp[k][s[(c+1)%2][j]];
c=(c+1)%2;q=d;d=0;//交换层次
}
}
C++语言
const int INT = 32767;
const int MAX = 10;
int dis[MAX];
int path[MAX];
int A[MAX][MAX];
void Dijk(int v)
{
bool S[MAX]; // 判断是否已存入该点到S集合中
int n=MAX;
for(int i=1; i<=n; ++i)
{
dis[i] = A[v][i];
S[i] = false; // 初始化
path[i] = v;
}
dis[v] = 0; S[v] = true;
for(int i=2; i<=n; i++)
{
int mindist = INT;
int u = v; // 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!S[j]) && dis[j]// u保存当前邻接点中距离最小的点的号码
mindist = dis[j];
}
S[u] = true;
for(int j=1; j<=n; j++)
if((!S[j]) && A[u][j]if(dis[u] + A[u][j] < dis[j]) //在通过新加入的u点路径找到离v点更短的路径
{
dis[j] = dis[u] + A[u][j]; //更新dist
path[j] = u; //记录前驱顶点
}
}
}
}
Matlab 语言
%迪杰斯特拉(单源)
% 最短距离 ,路径 距离矩阵 起始点 结束点
function [res,index] = Djsk(mp,stat,ends)
n=size(mp,1);
%初始化
bj=zeros(n,1); %标记初始化
dis=mp(stat,:); %各点最短路距离初始化
path=ones(n,1),path=path.*stat;%各点最短路路径初始化
dis(stat)=0;bj(stat)=1;
for i=1:n
min=Inf; k=1;%局部初始化
for j=1:n %从未找到最短路径点集合中找一个路径最短的点
if (bj(j)~=1)&&(dis(j)j);k=j;end
end
bj(k)=1;%标记已找到的点的最短路径
for j=1:n %用但前最短路节点更新未找到最短路的节点(同时更新各点路径的前一个点,即父节点)
if (bj(j)~=1)&&(dis(j)>(dis(k)+mp(k,j))), dis(j)=dis(k)+mp(k,j);path(j)=k;end
end
end
%对要求最短路径进行处理
tem=ends;index(1)=ends;i=2;
while path(tem)~=stat
index(i)=path(tem);
tem=path(tem);
i=i+1;
end
index(i)=stat;index=index(length(index):-1:1);res=dis(ends);
end

