最短路算法合集
单源最短路问题
单源最短路问题是指:求源点到图中其余各顶点的最短路径。
这类问题如果使用DFS求解效率会很慢,而使用BFS就多了一个边权为一的限制,否则就会出错
于是乎就有了单源最短路径算法
Dijkstra单源最短路径算法
算法主要流程
我们用dis[ i ]表示从源点 s 到节点 i 的最短路径,dis[ s ] = 0;
1.找到距离源点最近的一个节点v,放入集合U。
2.用dis[ v ]和当前边的边权更新从v能够到达的所有节点的dis值。这一步被我们称为松弛操作。
3.重复以上两个步骤,直到遍历完所有s能够到达的点为止。
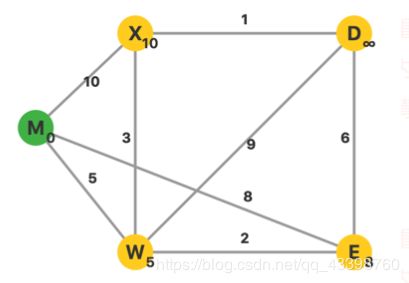
我们一起来看一个例子
这是一个带权图
首先,把源点放入集合中,进行松弛操作
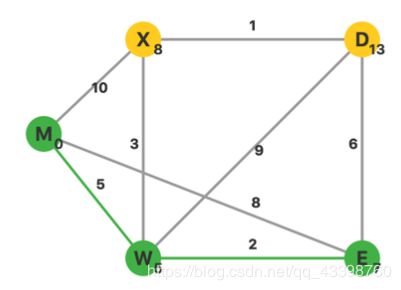
找到dis最小的节点为W,将W放入集合中,进行松弛操作
找到dis最小的节点为E,放入集合,进行松弛操作
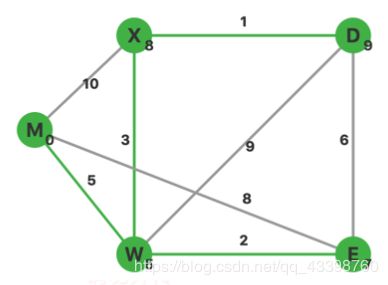
找到dis最小的节点为X,加入集合,进行松弛操作
以此类推
结束。
参考代码
#include
using namespace std;
struct edge {
int v, w, next;
} e[500010];
int head[10010], cnt;
int n, m, s;
int dis[10010];
bool vis[10010];
inline int read() {
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
void insert(int u, int v, int w) {
e[++cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt;
}
void dijkstra(int u) {
dis[u] = 0;
while (!vis[u]) {
vis[u] = 1;
for (int i = head[u]; i; i = e[i].next) {
if (!vis[e[i].v] && dis[e[i].v] > dis[u] + e[i].w) {
dis[e[i].v] = dis[u] + e[i].w;
}
}
int mini = 1e9;
for (int i = 1; i <= n; i++) {
if (!vis[i] && dis[i] < mini) {
mini = dis[i];
u = i;
}
}
}
}
int main() {
n = read(), m = read(), s = read();
while (m--) {
int a = read(), b = read(), c = read();
insert(a, b, c);
}
for (int i = 1; i <= n; i++) dis[i] = 2147483647;
dijkstra(s);
for (int i = 1; i <= n; i++) printf("%d ", dis[i]);
return 0;
} Dijkstra的堆优化
朴素的Dijkstra算法暴力枚举dis值最小的点,时间复杂度较高
枚举时的过多开销是可以避免的
我们可以使用堆来对这一过程进行优化
示例代码
const int MAX_N =10000;
const int MAX_M =100000;
const int inf =0x3f3f3f3f;
struct edge {
int v, w, next;
} e[MAX_M];
int p[MAX_N], eid, n;
void mapinit() {
memset(p,-1,sizeof(p));
eid =0;
}
void insert(int u,int v,int w) { // 插入带权有向边
e[eid].v = v;
e[eid].w = w;
e[eid].next = p[u];
p[u]= eid++;
}
void insert2(int u,int v,int w) { // 插入带权双向边
insert(u, v, w);
insert(v, u, w);
}
typedef pair PII;
set> min_heap;
int dist[MAX_N];// 存储单源最短路的结果
bool vst[MAX_N];// 标记每个顶点是否在集合 U 中
bool dijkstra(int s) { // 初始化 dist、小根堆和集合 U
memset(vst,0,sizeof(vst));
memset(dist,0x3f,sizeof(dist));
min_heap.insert(make_pair(0, s));
dist[s]=0;
for(int i =0; i < n; ++i) {
if(min_heap.size()==0) { // 如果小根堆中没有可用顶点,说明有顶点无法从源点到达,算法结束
return false;
}// 获取堆顶元素,并将堆顶元素从堆中删除
set>::iterator iter = min_heap.begin();
int v = iter->second;
min_heap.erase(*iter);
vst[v]=true;// 进行和普通 dijkstra 算法类似的松弛操作
for(int j = p[v]; j !=-1; j = e[j].next) {
int x = e[j].v;
if(!vst[x]&& dist[v]+ e[j].w < dist[x]) { // 先将对应的 pair 从堆中删除,再将更新后的 pair 插入堆
min_heap.erase(make_pair(dist[x], x));
dist[x]= dist[v]+ e[j].w;
min_heap.insert(make_pair(dist[x], x));
}
}
}
return true;// 存储单源最短路的结果} 我个人更喜欢用单调队列进行优化
代码
#include
using namespace std;
struct edge {
int v, w, next;
} e[200010];
int head[100010], cnt;
int n, m, s;
int dis[100010];
inline int read() {
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
void insert(int u, int v, int w) {
e[++cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt;
}
struct node {
int f, s;
node () {}
node (int ff, int ss) {
f = ff;
s = ss;
}
bool operator < (const node & x) const {
return x.s < s;
}
};
priority_queue q;
void dijkstra(int u) {
memset(dis, 0x3f3f3f3f, sizeof dis);
dis[u] = 0;
q.push(node(u, 0));
while (!q.empty()) {
node x = q.top();
q.pop();
int f = x.f, s = x.s;
if (s != dis[f]) continue;
for (int i = head[f]; i; i = e[i].next) {
int v = e[i].v, w = e[i].w;
if (dis[v] > dis[f] + w) {
dis[v] = dis[f] + w;
q.push(node(v, dis[v]));
}
}
}
}
int main() {
n = read(), m = read(), s = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
insert(u, v, w);
}
dijkstra(s);
for (int i = 1; i <= n; i++) {
cout << dis[i] << " ";
}
return 0;
} SPFA单源最短路径算法
算法主要流程
用dis[ i ]表示从源点到 i 的最短路径,使用队列存储从当前位置可能到达的所有拓展位置,同时用一个bool数组inq表示节点 i 是否在队列中。
1.将源点加入队列,dis[ s ] = 0;
2.取出队首元素,若dis[ u ] + w < dis[ v ], dis[ v ] = dis[ u ] + w;
若v不在队列中,将其入队
3.重复步骤2直到队列为空
算法主要思想
我们不难发现,将当前节点的每一个拓展节点放入一个队列中,然后依次取用其实是BFS的思想。
从一定程度上我们可以认为SPFA是由BFS转化而来。也就是说,把边权为一的BFS推广到带权图上就得到了SPFA。
唯一的区别是BFS只要第一次访问到就能保证是最短路,而SPFA都要不断地更新最短路。
SPFA算法本质上是Bellman-ford的队列优化,国外一般不认为它是一个新的算法。
代码
void spfa(int u) {
memset(dis, 1e9, sizeof dis);
inq[u] = true;
dis[u] = 0;
queue q;
q.push(u);
while (!q.empty()) {
u = q.front();
q.pop();
inq[u] = false;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].v, w = e[i].w;
if (dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
if (!inq[v]) {
q.push(v);
inq[v] = true;
}
}
}
}
} SPFA判负环
记录每个节点入队次数,若大于n,则表示存在负环
代码
bool spfa(int u) {
memset(dis, 1e9, sizeof dis);
inq[u] = true;
dis[u] = 0;
queue q;
q.push(u);
while (!q.empty()) {
u = q.front();
q.pop();
inq[u] = false;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].v, w = e[i].w;
if (dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
if (!inq[v]) {
q.push(v);
inq[v] = true;
++in[v];
if (in[v] > n) {
return true;
}
}
}
}
}
return false;
} Floyd多源最短路径算法
概述
这个算法简单来说就是利用动态规划进行批量处理。它具有高效,代码简短的优势,比较常用
我们用dp[ k ][ i ][ j ]表示i到j能经过1 ~ k的点的最短路。
那么实际上dp[ 0 ][ i ][ j ]就是原图,如果i, j之间存在边,那么i, j之间不经过任何点的最短路就是边长
否则,i, j之间的最短路为无穷大
所以就有转移方程
dp[ k ][ i ][ j ] = min(dp[ k - 1 ][ i ][ j ], dp[ k - 1 ][ i ][ k ] + dp[ k - 1 ][ k ][ j ])
我们再分析就会发现,dp[k] 只能由 dp[k - 1]转移而来。
所以,状态转移方程可以进一步简化为
dp[ i ][ j ] = min(dp[ i ][ j ], dp[ i ][ k ] + dp[ k ][ j ]);
代码
int g[N][N];
void floyd(int n) {
for(int k =1; k <= n; ++k) {
for(int i =1; i <= n; ++i) {
for(int j =1; j <= n; ++j) {
g[i][j]=min(g[i][j], g[i][k]+ g[k][j]);
}
}
}
}