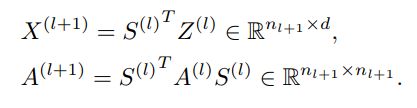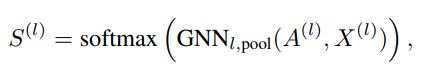《Hierarchical Graph Representation Learning with Differentiable Pooling》论文解析

    最近阅读了由斯坦福大学研究团队发表的这篇名为“Hierarchical graph representation learning with differentiable pooling”论文，对于论文中提出的问题觉得十分新颖，同时论文的写作也很流畅，因此将个人对该论文的理解进行整理，如有不当之处还请指教。

    算法框架

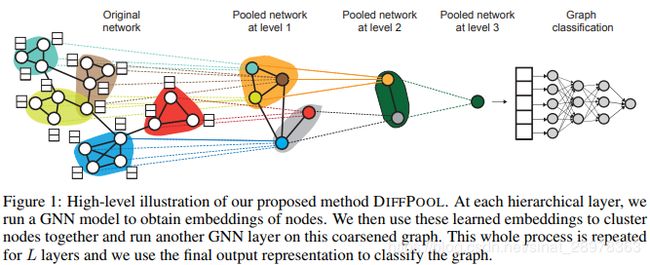
    GNN的相关研究被广泛的应用于图表示学习中，并且在节点分类和链路预测等任务中取得了SOTA的结果。但是GNN框架设计之初是基于CNN实现的，其固有的扁平化结构并不能完全适应于图的表示，因为大多数的图（网络）是具有层次结构的。所以，本文的motivation也是源于图的这种分层结构，提出了一种名为DIFFPOOL的算法。算法的总体框架如图1所示。

    从图1可以看出，DIFFPOOL算法是一种分层pooling的GNN算法。在每一层内部使用的是一种图分类表示算法（本文使用GRAPHSAGE模型【“Inductive representation learning on large graphs”】）来得到当前图中节点的向量表示；在层与层之间则使用局部pooling的操作得到当前图的粗化图（coarsened graph）。在每一层内，算法都会根据GNN得到的节点向量对该层中的图进行聚类操作，将节点映射到一系列类别（cluster）中，从而得到新的分层图。直到最后一层，DIFFPOOL算法会得到整个图的一个统一的向量表示，用于图分类任务。DIFFPOOL算法的核心思想是通过提供一个能够区分图中分层节点的pooling操作来得到一个更深、更多层结构的GNN模型。同时DIFFPOOL算法能够和多种GNN模型进行融合，也说明该算法具有一定的泛化性。

    算法介绍

预备知识

1、图分类任务。将一个图G表示成(A，F)，其中A为图的邻接矩阵 ,F表示图的节点特征矩阵 ,n 为图中节点的个数，d为节点的特征数（当然，对于一个图的表示可以根据模型需要自行定义，本文使用的是邻接矩阵和特征矩阵的方式表示所要输入的图）。而一个图分类任务可以有如下描述：给出一系列的带标签的图 ,其中  为每个图  所对应的标签。图分类任务则是需要学习从G到Y的一个映射函数。 但是，与传统的监督式机器学习算法相比，如何使用神经网络结构提取到有用的图分类特征是具有很大挑战的。

2、图神经网络（GNN）。GNN模型通常是一种“信息传递”的结构，如  。其中是指经过k步GNN后得到的网络节点向量（也就是信息）；M是信息传递函数，它依赖于图的邻接矩阵。θ是可训练的参数。信息传递过程是一种信息自身的迭代计算，当前信息是由其前一步信息计算得到的。对于信息传递函数M, 它有很多的实现可能。在GCN模型【参考文献3】中，M是用一个线性变换和ReLU函数实现的，如。其中，，，是可训练的矩阵。

论文的目的是寻找一个通用的、端到端的区分策略以完成图节点的分层表示，因此对于GNN模型中的信息传递函数M的实现并不是重点（实质上，图节点向量化是通过现有的成熟模型得到的）。本文的研究内容主要是：

1. 给定一个GNN的输出 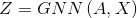 （X是图节点的初始输入特征，最初的X就是上文中的F，但随着计算过程的推进，X是变化的；Z是经过GNN后输出的图节点特征，第l+1层中的X是第l层的输出Z）和一个图的邻接矩阵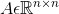，需要输出一个与当前层中的图相对应的粗化图（邻接矩阵A变为mm维的，节点向量Z变为md维的），然后这个当前层的输出作为下一层的输入。这样的一个过程可能会持续L次，从而在越来越粗化的图表示中产生一个L层的GNN模型。正如图1所表示的那样。
2. 论文的目的是寻求一个可以更好的聚类图节点的GNN算法，并将这个节点聚类后的粗化图作为下一层GNN的输入。

算法实现

想要实现上面所论述的目的，则必须要学习一个聚类分配矩阵（cluster assignment matrix）,这个矩阵的作用便是把当前层中图节点进行聚类，将其分配到一个更粗化的类别中（也就是根据聚类分配矩阵的pooling过程）。所以，当前层中的图节点向量化表示的好坏决定了聚类分配矩阵学习的优劣。因此，为了得到质量更高的节点向量，论文使用GNN算法来学习对于图分类和图分层pooling最有效的向量信息。

Q1: 假定聚类分配矩阵已存在，如何进行Pooling？

定义在第l层中的聚类分配矩阵。的每一行代表的是当前层（l）中的节点（或者类别），每一列代表下一层（l+1）中定义的节点（类别）数。例如，在当前层中的图节点数（节点类别数）为100，欲希望在下一层中得到的节点数（类别数）为25，则是一个100×25的矩阵。同时，定义当前层的输入邻接矩阵为和节点向量矩阵为。那么在这些输入的前提下，DIFFPOOL算法将会产生一个新的邻接矩阵（该邻接矩阵中的节点数一般明显小于输入邻接矩阵的节点数）和新的节点向量矩阵，即。其中DIFFPOOL的过程可用如下公式表示。

上述两个公式分别将输入的节点向量矩阵聚集为新的节点向量和计算得到粗化图的邻接矩阵。

Q2: 怎样学习聚类分配矩阵？

聚类分配矩阵同样是使用一个GNN来学习得到。公式如下。

其中softmax是一个逐行计算的softmax函数，输出的类别数是预定义好的类别最大数。

为了使以上两个问题能够充分学习，论文引入了链路预测任务和信息熵归一化两个辅助任务进行loss函数的学习。

    实验结果

数据集

论文使用了多个数据集进行图分类任务，主要有蛋白质数据集（ENZYMES，PROTEINS，D&D）、社会网络数据集（REDDIT_MULTI_12K）和科学合作网络数据集（COLLAB）。

模型配置

在论文的图分类实验中，用于学习节点向量的GNN模型是GRAPHSAGE算法（因为作者发现GRAPHSAGE算法的性能要优于GCN），在该算法的上层搭建本文所提出的DIFFPOOL层用于对图节点进行分层Pooling。具体的结构框架为：

1. 在每两层的的GRAPHSAGE后增加一个DIFFPOOL层
2. 一共设置两层DIFFPOOL层，第一层的DIFFPOOL设置的聚类数为该层输入节点数的10%，第二层的DIFFPOOL设置的聚类数为25%。对于小数据集（ENZYMES，PROTEINS和COLLAB等），一层的DIFFPOOL同样可以取得很好的结果。
3. 在每一层的DIFFPOOL之后，会接一个三层的图卷积操作用于强化节点的向量表示

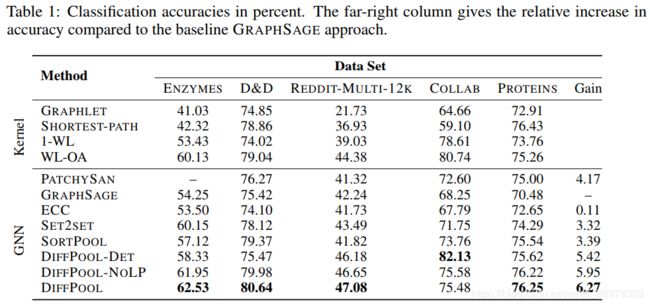
在每一层的GRAPHSAGE中均采用batch normal操作，并在节点向量的训练过程中加上L2范数用于稳定训练。所有数据集上的训练轮数为3000。对比实验方法有GRAPHSAGE、STRUCTURE2VEC、ECC等边聚类方法、PATCHYSAN、SET2SET和SORTPOOL等。具体的分类结果如表1所示。

 

其中，Gain列表示DIFFPOOL算法与其他算法相比所提高精度的平均值。可达到6.27%。

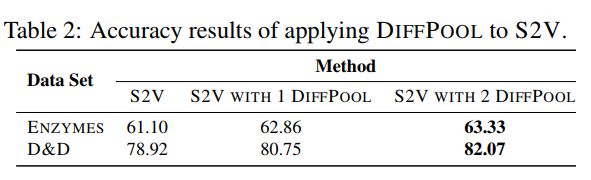
同时，作者也做了泛化性实验：将DIFFPOOL层应用于STRUCTURE2VEC算法进行准确性的分析。实验结果如表2所示。

结论

DIFFPOOL算法是一种图分层表示的算法，用于图分类实验。该算法的目标是寻求一种优良的图节点分类算法和节点表示算法，提供一种端到端的图分类学习模型。算法在多个数据集上都表现出了很好的性能。但是作者也提出，目前工作中对于图节点分类算法还比较粗糙，因此未来还有很多工作可以在此基础上进行。