数学建模之非线性规划
1. 定义
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问 题。
非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。
一般形式:


2. 非线性规划的 Matlab 解法
Matlab 中非线性规划的数学模型写成以下形式

lb<=x<=ub
其中 f (x)是标量函数,A,B,Aeq,Beq是相应维数的矩阵和向量,C(x),Ceq是非线性向量函数。
Matlab中的命令是 [x,fval]=fmincon(fun,x0,A,B,Aeq,Beq,lb,ub,nonlcon,options)
例:求下列非线性规划


3. 约束极值问题
带有约束条件的极值问题称为约束极值问题,也叫规划问题。
3.1 二次规划
若某非线性规划的目标函数为自变量x的二次函数,约束条件又全是线性的,就称 这种规划为二次规划。
Matlab 中二次规划的数学模型可表述如下:
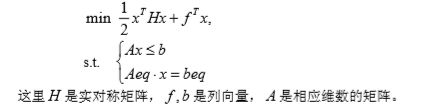
Matlab 中求解二次规划的命令是
[x,fval]=quadprog(H,f,A,b,Aeq,Beq,lb,ub,x0,options)
(具体细节可以参看在 Matlab 指令中运行 help quadprog 后的帮助)。
例: 求解二次规划
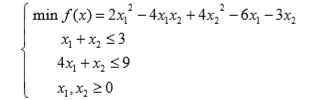
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))求得x1=1.9500,x2=1.0500,minf(x)=-11.0250
3.2 罚函数法
利用罚函数法,可将非线性规划问题的求解,转化为求解一系列无约束极值问题, 因而也称这种方法为序列无约束小化技术,简记为 SUMT .
罚函数法求解非线性规划问题的思想是,利用问题中的约束函数作出适当的罚函 数,由此构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。主要有两种形式,一种叫外罚函数法,另一种叫内罚函数法,下面介绍外罚函数法。

例: 求下列非线性规划

(1)定义增广目标函数,编写 M 文件 test.m
function g=test1(x);
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2); 或者是利用Matlab的求矩阵的极小值和极大值函数编写test.m如下:
function g=test2(x);
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*sum(min([x';zeros(1,2)]))-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2); 也可以修改罚函数的定义,编写test.m如下
function g=test3(x);
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(min(x),0)-M*min(x(1)^2-x(2),0)+M*(-x(1)-x(2)^2+2)^2; (2)求增广目标函数的极小值,在 Matlab 命令窗口输入
[x,y]=fminunc('test3',rand(2,1)) 由于是非线性问题,很难求得问题的全局最优解,因此只能求得局部最优解,并且每次运行结果都不一样.
注:(1)如果非线性规划问题要求实时算法,则可以使用罚函数方法,但计算精度较低;
(2)如果非线性规划问题不要求实时算法,但要求精度高,则可以使用Lingo软件编程求解或使用Matlab的fmincon命令
Matlab优化工具箱中的optimtool命令提供了优化问题的用户图形界面解法。 optimtool可应用到所有优化问题的求解,计算结果可以输出到Matlab工作空间中。