Pure Pursuit 纯跟踪控制算法
阿克曼转向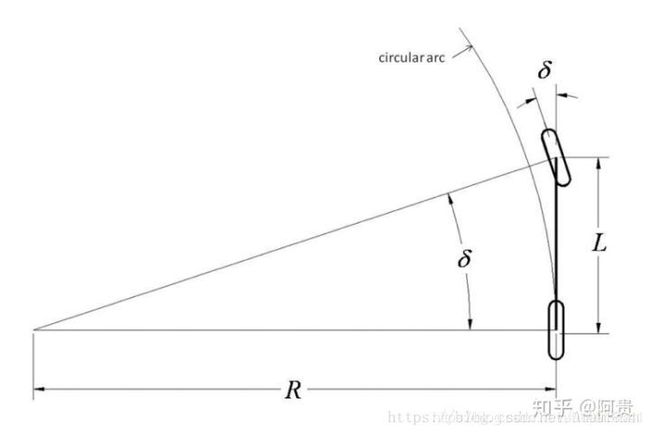 阿克曼结构前轮来控制转向
阿克曼结构前轮来控制转向
假设车沿着R的半径在旋转,车身前轮到后轮轴距L,因为车在旋转
重点理解这句话
所以前轮的方向始终是该圆周的切线,遵循曲率
所以得到前轮的转角应该为
t a n ( δ ) = L R tan(\delta)=\frac{L}{R} tan(δ)=RL
路径跟踪算法
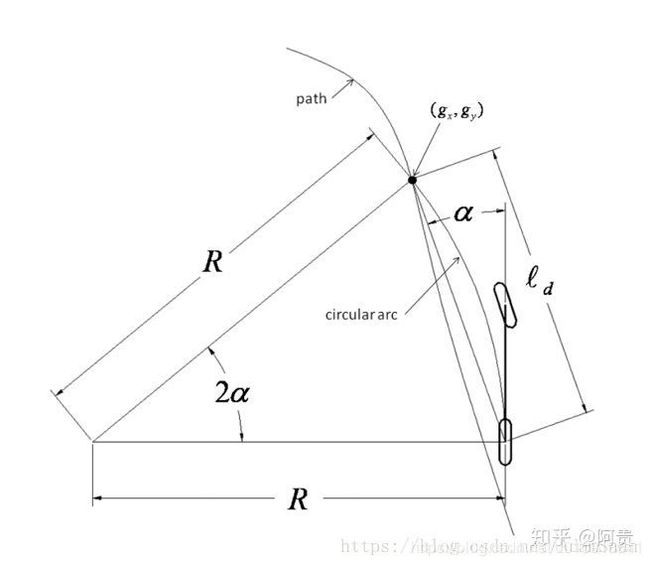 以车轮后中心为点,需要该机器经过该目标点gx gy,
以车轮后中心为点,需要该机器经过该目标点gx gy,
ld:当前点到要跟随目标点的距离
α \alpha α:当前的方向和到目标点的方向差
三角公式可得一下函数
l d s i n ( 2 α ) = R s i n ( 90 − α ) \frac{ld}{sin(2\alpha)}=\frac{R}{sin(90-\alpha)} sin(2α)ld=sin(90−α)R
简化一下如下
R = l d 2 s i n ( α ) R=\frac{ld}{2sin(\alpha)} R=2sin(α)ld
两轮差速路径跟随组合公式
假如是两轮机器人,没有轴距 即可得到机器人路径跟随的算法
R = l d 2 s i n ( α ) R=\frac{ld}{2sin(\alpha)} R=2sin(α)ld
R = v w R=\frac{v}{w} R=wv
两者结合,消除R
==>
v w = l d 2 s i n ( α ) \frac{v}{w}=\frac{ld}{2sin(\alpha)} wv=2sin(α)ld
再结合DWA算法 就可以仿真出来一组基于当前ld ,的vw 集合,最后选择比较好的路径算法
阿克曼路径角度输出
结合这两个公式 组合推算当前控制角度
t a n ( δ ) = L R tan(\delta)=\frac{L}{R} tan(δ)=RL
R = l d 2 s i n ( α ) R=\frac{ld}{2sin(\alpha)} R=2sin(α)ld
两个公式 结合消除R ==>
ld:当前点到要跟随目标点的距离,该值是根据当前点和目标点的位置,计算得出
α \alpha α:当前的方向和到目标点的方向差, 该值是根据当前航向角和目标点的位置,计算得出
L:阿克曼车型轴间距,前轮中心到后轮中心的距离
t a n ( δ ) = 2 L s i n ( α ) l d tan(\delta)=\frac{2Lsin(\alpha)}{ld} tan(δ)=ld2Lsin(α)
在具体的实际情况中,ld 即目标跟随点的位置是根据弧度在发生变化的
可以用
l = k v ( t ) l=kv(t) l=kv(t)
具体代码测试
https://github.com/AGV-IIT-KGP/PythonRobotics/tree/master/PathTracking/pure_pursuit
参考
https://zhuanlan.zhihu.com/p/48117381