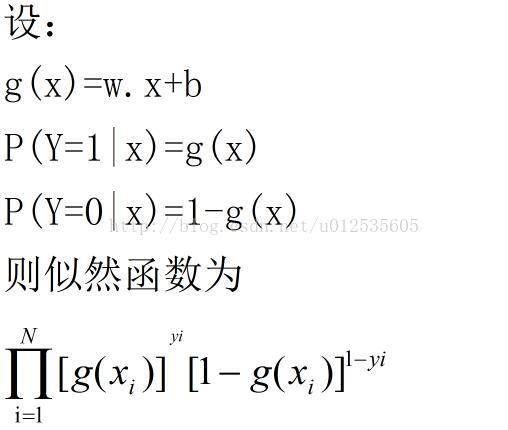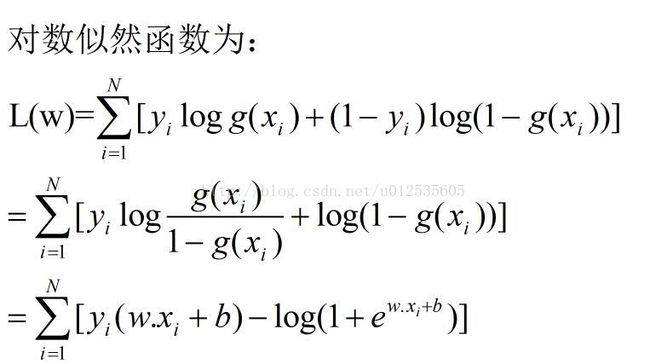分类算法----逻辑回归Logistic原理和Python实现学习笔记

1 什么是逻辑回归

Logistic属于概率型非线性回归，分为二分类和多分类的回归模型。对于二分类的逻辑回归只有是和否两个取值，记为1和0,在自变量xi(i从1到n)，y取是的概率为P，y取否的概率为1-P，研究的是当y取是发生的概率p与xi的关系

逻辑回归优点：
1）预测结果是介于0和1之间的概率；
2）可以适用于连续性和类别性自变量；
3）容易使用和解释；
缺点：
1）对模型中自变量多重共线性较为敏感，在数据选择前需对变量的相关性做处理。以减少候选变量之间的相关性；
2）预测结果呈“S”型，因此从log(odds)向概率转化的过程是非线性的，在两端随着​log(odds)值的变化，
概率变化很小，边际值太小，slope太小，而中间概率的变化很大，很敏感。 
导致很多区间的变量变化对目标概率的影响没有区分度，无法确定阀值。

2 Logistic函数

Logistic回归模型中的因变量只有1-0（假设为二分类问题）两种取值，y取1的概率为p，y取0概率为1-p，1和0的概率之比称为优势比（odds）即为p/(1-p)对优势比取自然对数即得Logistic变换

逻辑函数的图形展示如下所示，

3逻辑回归模型

4 模型参数估计

在学习逻辑回归模型时，对于给定的训练数据集T={（x1,y1）,(x2,y2)...(xn,yn)}，可以应用极大似然估计法估计模型参数，从而得到逻辑回归模型。

备注：为方便计算设b=0

5 利用梯度上升算法求L(W)的极大值

至此逻辑回归推到基本完成，接下来就学习逻辑回归的底层实现

6 逻辑回归的底层实现

参考机器学习实战

from numpy import *
import matplotlib.pyplot as plt
import pandas as pd
def loadDataSet():
    dataMat=[]
    labelMat=[]
    fr=open('testSet.txt')#读文件
    for line in fr.readlines():#遍历文件的每一条记录
        lineArr=line.strip().split()#拆分字段
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])#添加到列表中
        labelMat.append(int(lineArr[2]))#分类标签
    return dataMat,labelMat
    
def sigmoid(inX):
    return 1.0/(1+exp(-inX))
# #计算系数   
def gradAscent(dataMatIn,classLabels):
    dataMatrix=mat(dataMatIn)
    labelMat=mat(classLabels).transpose()#矩阵转置
    m,n=shape(dataMatrix)
    alpha=0.001
    maxCycles=500
    data=[]
    weights=ones((n,1))
    for k in range(maxCycles):   
        h=sigmoid(dataMatrix*weights)#sigmoid函数
        error=(labelMat-h)#预测误差
        weights=weights+alpha*dataMatrix.transpose()*error#求系数
        data.append([k,pd.DataFrame(weights).ix[0]])
        print k
    plt.plot(pd.DataFrame(data)[0],pd.DataFrame(data)[1])
    plt.show()  
    return weights
    
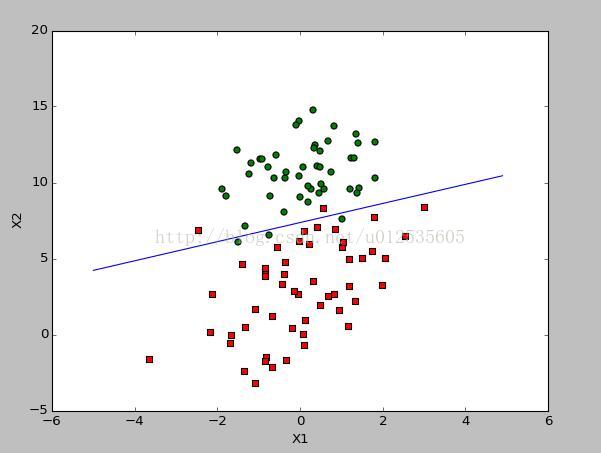
##图形显示各分类效果   
def plotBestFit(weights):  
    dataMat,labelMat=loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-5.0, 5.0, 0.1)
    y = (-pd.DataFrame(weights).ix[0]-pd.DataFrame(weights).ix[1]*pd.DataFrame(x))/(pd.DataFrame(weights).ix[2])
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

分类结果如下图所示，迭代500次结果

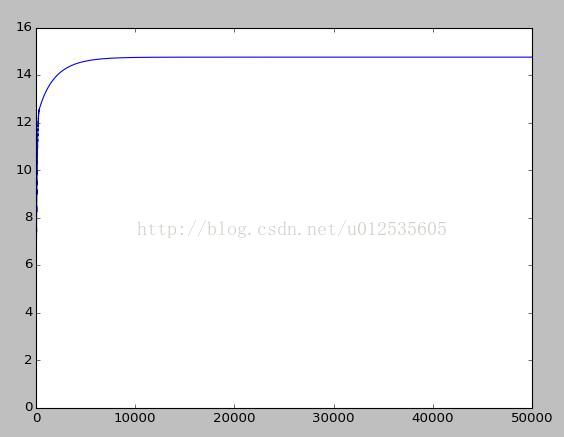
在a=0.001,迭代5000次模型依然没有收敛

在迭代50000次模型如下所示：在a=0.001收敛速度较慢

增大a值为0.01，迭代50000次如下图所示

后续有随机梯度上升和改进的随机梯度上升算大均大同小异，随机梯度上升：一次仅用一个样本来更新回归系数，改进的随机梯度：设置参数a与迭代次数和数据量之间的数学关系，通过随机选取样本来更新回归系数，以减少周期性的波动