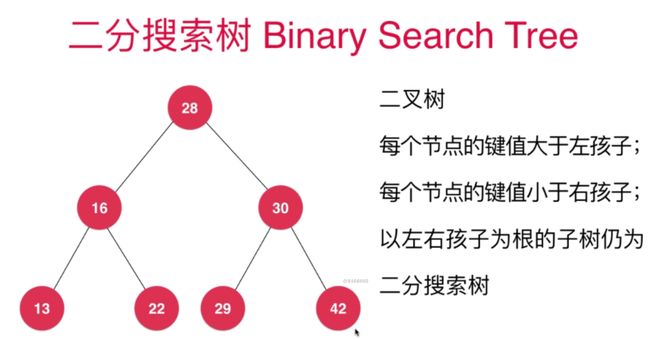
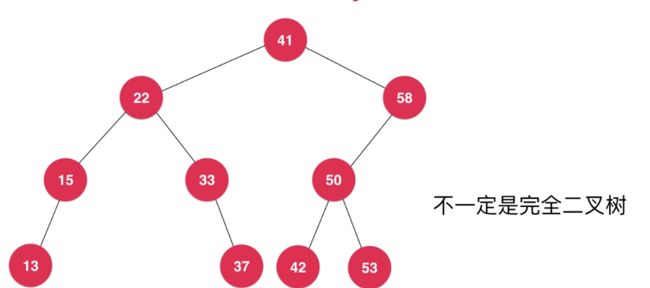
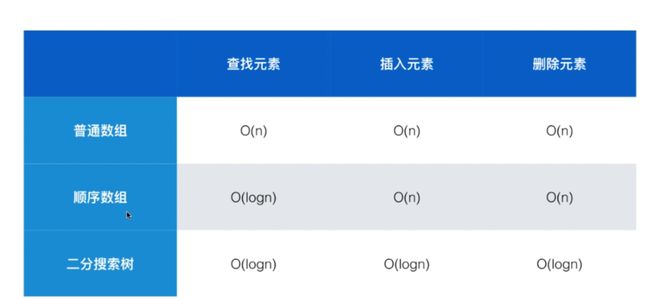
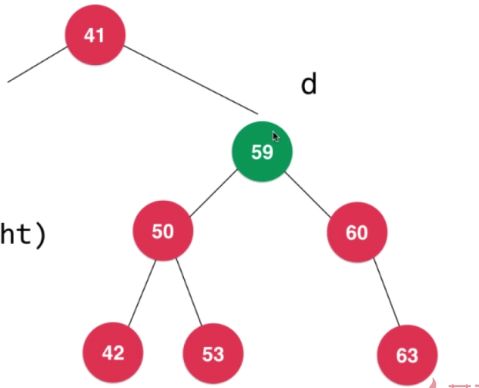
插入操作:
与根节点比较相等则覆盖其值,若小于则与左节点比较,若大与则与右节点比较,若根节点为空则插入这个位置即可。递归重复即可。
查找操作
与根节点比较相等,若根节点为空,则返回false,若大于根节点则与右节点比较
若小于则与左节点比较,若等于则返回节点的值,以此递归即可。
遍历
深度优先遍历:
中序遍历出来的是排序好的队列
后序遍历是用来删除节点用的
广度优先遍历
以上的算法实现
package bobo.algo;
// 二分搜索树
// 由于Key需要能够进行比较,所以需要extends Comparable
public class BST, Value> {
// 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
private class Node {
private Key key;
private Value value;
private Node left, right;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
left = right =null;
}
}
private Node root; // 根节点
private int count; // 树种的节点个数
// 构造函数, 默认构造一棵空二分搜索树
public BST() {
root =null;
count =0;
}
// 返回二分搜索树的节点个数
public int size() {
return count;
}
// 返回二分搜索树是否为空
public boolean isEmpty() {
return count ==0;
}
// 向二分搜索树中插入一个新的(key, value)数据对
public void insert(Key key, Value value){
root = insert(root, key, value);
}
// 查看二分搜索树中是否存在键key
public boolean contain(Key key){
return contain(root, key);
}
// 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
public Value search(Key key){
return search( root, key );
}
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
//********************
//* 二分搜索树的辅助函数
//********************
// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
private Node insert(Node node, Key key, Value value){
if( node ==null ){
count ++;
return new Node(key, value);
}
if( key.compareTo(node.key) ==0 )
node.value = value;
else if( key.compareTo(node.key) <0 )
node.left = insert( node.left, key, value);
else // key > node->key
node.right = insert( node.right, key, value);
return node;
}
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain(Node node, Key key){
if( node ==null )
return false;
if( key.compareTo(node.key) ==0 )
return true;
else if( key.compareTo(node.key) <0 )
return contain( node.left, key );
else // key > node->key
return contain( node.right, key );
}
// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search(Node node, Key key){
if( node ==null )
return null;
if( key.compareTo(node.key) ==0 )
return node.value;
else if( key.compareTo(node.key) <0 )
return search( node.left, key );
else // key > node->key
return search( node.right, key );
}
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder(Node node){
if( node !=null ){
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder(Node node){
if( node !=null ){
inOrder(node.left);
System.out.println(node.key);
inOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder(Node node){
if( node !=null ){
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
// 测试二分搜索树
public static void main(String[] args) {
int N =1000000;
// 创建一个数组,包含[0...N)的所有元素
Integer[] arr =new Integer[N];
for(int i =0 ; i < N; i ++)
arr[i] =new Integer(i);
// 打乱数组顺序
for(int i =0 ; i < N; i ++){
int pos = (int) (Math.random() * (i+1));
Integer t = arr[pos];
arr[pos] = arr[i];
arr[i] = t;
}
// 由于我们实现的二分搜索树不是平衡二叉树,
// 所以如果按照顺序插入一组数据,我们的二分搜索树会退化成为一个链表
// 平衡二叉树的实现,我们在这个课程中没有涉及,
// 有兴趣的同学可以查看资料自学诸如红黑树的实现
// 以后有机会,我会在别的课程里向大家介绍平衡二叉树的实现的:)
// 我们测试用的的二分搜索树的键类型为Integer,值类型为String
// 键值的对应关系为每个整型对应代表这个整型的字符串
BST bst =new BST();
for(int i =0 ; i < N; i ++)
bst.insert(new Integer(arr[i]), Integer.toString(arr[i]));
// 对[0...2*N)的所有整型测试在二分搜索树中查找
// 若i在[0...N)之间,则能查找到整型所对应的字符串
// 若i在[N...2*N)之间,则结果为null
for(int i =0 ; i <2*N; i ++){
String res = bst.search(new Integer(i));
if( i < N )
assert res.equals(Integer.toString(i));
else
assert res ==null;
}
}
}
广度优先遍历就是先建造一个队列(先进先出)
首先将根节点加入队列,移除根节点(遍历)的同时加入左右节点,遍历左节点将左节点的左右子节点加入到队列,再遍历右节点同时将右节点的左右子节点加入队列,以此类推。
// 二分搜索树的层序遍历
public void levelOrder(){
// 我们使用LinkedList来作为我们的队列
Queue q =new LinkedList();
q.add(root);
while( !q.isEmpty() ){
Node node = q.remove();
System.out.println(node.key);
if( node.left !=null )
q.add( node.left );
if( node.right !=null )
q.add( node.right );
}
}
删除二分搜索树的最小值和最大值
先找到最小值,最小值一定是最左边的节点,一直遍历左子树,最后一个非空即为最小节点,要防止的是其还有右子节点,如果没有右子节点直接删除即可,有的话将其右节点放在它原来的位置即可。删除最大节点要防止其有左节点,若有的话,将其左节点放在原来它的位置即可,若无,则直接删除即可。
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left ==null ){
Node rightNode = node.right;
node.right =null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if( node.right ==null ){
Node leftNode = node.left;
node.left =null;
count --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
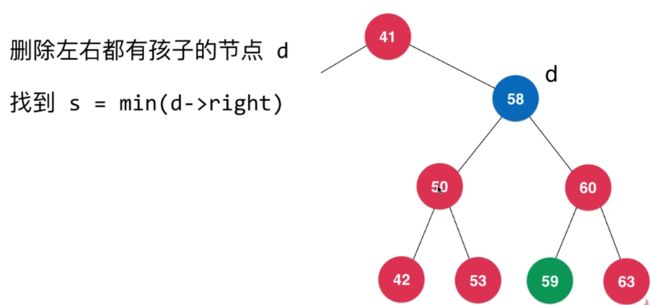
删除随便一个节点
找出右子树中最小的数,替换原来的位置。
// 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node remove(Node node, Key key){
if( node ==null )
return null;
if( key.compareTo(node.key) <0 ){
node.left = remove( node.left, key );
return node;
}
else if( key.compareTo(node.key) >0 ){
node.right = remove( node.right, key );
return node;
}
else{// key == node->key
// 待删除节点左子树为空的情况
if( node.left ==null ){
Node rightNode = node.right;
node.right =null;
count --;
return rightNode;
}
// 待删除节点右子树为空的情况
if( node.right ==null ){
Node leftNode = node.left;
node.left =null;
count--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor =new Node(minimum(node.right));
count ++;
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right =null;
count --;
return successor;
}
}
二叉搜索树在极端的情况下如0123456789下变成链表,所以采用平衡树解决这个问题即可如红黑树