数学也荒唐：20个脑洞大开的数学趣题

内容简介

本书用20个数学问题探讨了代数、概率学、统计学、平面几何、图论、拓扑学等主题，在意想不到的趣题中探讨数学难题，让貌似艰涩的数学显得轻松有趣，让貌似荒唐可笑的问题展示数学的乐趣。

• 法国“搞怪”数学网红博客佳作
  
• 法国亚马逊数学类畅销书
  
• 脑洞大开的荒唐问题，另类的数学研究，启发心智的思考
  
• 令人捧腹的笑话，丰富的漫画，让数学不再枯燥晦涩

作者简介

杰罗姆 · 科唐索 （Jérôme Cottanceau），数学教师，创作了法国知名数学博客“花椰菜”，凭借幽默风趣的叙述风格，广受中学生和大学生的欢迎。

本书内容

前言

数学有什么用？

从事数学工作的人总被问起：数学有什么用？不管是学者、教授、学生还是普通的爱好者，总得为自己喜欢数学找个理由。有些人问得还算坦诚，比如：“代数是用来做什么的？”或者：“统计还有点用处，但我真不知道函数能有什么用。”有些人则略带嘲讽：“我真搞不懂数学，这玩意儿什么用也没有。”或者：“现在都有计算器了，还研究个什么劲儿啊？”这些话确实有些恼人，那该如何回答呢？

我们大致可以从两方面反驳“数学无用论”。一方面，可以说说数学的实际用途：比如，数论[1]就是加密的基础，没有加密，银行交易就会十分不安全，而代数[2]和逻辑则是信息科学不可分割的一部分；金融中要用到概率，生物学家也要用概率来分析生物可能的进化过程；有了图论，全球定位系统（GPS）才能找出道路网络上两点之间的最短路线；更不用说分析学[3]和物理学之间的紧密关系了。

另一方面，我们可以让人感受一下“数学之美”。这里不是要说“自相似”的分形几何之美，如宝塔花菜的奇妙外形或布列塔尼蜿蜒曲折的海岸线，也不是为人津津乐道的黄金比例——传说中，是它造就了古希腊帕特农神庙的完美比例，而且我们的银行卡也是按它制作的。“数学之美”不是视觉上的美，而是数学给人带来的精神愉悦。如果一个公式能把两个相去甚远的领域联系起来，我们就可以称之为“美”。比如，等式1+1/2²+1/3²+1/4²+…=π²/6把 π 与无穷数列联系了起来。如果一个证明简洁奇妙，另辟蹊径，那也可以说它十分优美。但是，如果对方认定了数学没什么用，那以上这些回答都不能让他满意。制造手机当然需要许多软件和硬件方面的数学知识，但手机用户完全不用懂得那么多。欧拉恒等式在数学家眼里十分优美，因为它把所有数学基本常数囊括在一个公式里，但在普通人看来，这没有什么了不起的。

那些问“数学有什么用”的人，是想让别人用一句话点醒他，为什么会有人对这些抽象的问题乐此不疲，而不管有没有实际意义？数学专业人士或者爱好者能给的答案也只有自己由衷的喜爱之情了，而正是这种喜爱之情，反而能让旁人认同。有人喜欢数学，有人喜欢收集迪士尼小徽章，这在本质上没有什么不同。

现在，让我们试着从第三个角度来回答“数学有什么用”的问题。这本书深入浅出地列举了数学在日常生活中的“具体”应用。但要注意的是，某些对数学家来说很具体的问题，在普通人看来可能并非如此。下面说到的问题包括怎么贴瓷砖、怎么摞煎饼、怎么让民主更民主一些、怎么闭着眼睛赢得法网公开赛，等等。当然，还有最重要的问题：上厕所的时候怎么选择小便器。数学能解决这么多荒唐的趣题，还需要找什么具体应用呢？

---

[1] 数论研究整数的性质及其运算，如质数、平方等。

[2] 代数可定义为研究数学对象之间变换关系的科学，如几何中的对称就是一种变换关系。

[3] 分析学是数学的一个分支，研究函数的性质及其变换，如极限、连续、导数、积分等。

01　早餐代表我的心

“亲爱的，天亮了，今天是2月14号，我特意为你准备了早餐。不用起床了，就在床上吃。好丰盛的，有刚出炉还冒着热气的羊角面包，有一大杯我刚刚亲手榨的橙汁，有新鲜水果，还有最重要的，一大碗牛奶！”

“你对我太好了，但为什么有牛奶呢？你知道我喝牛奶不消化啊……”

“很简单啊，因为这碗牛奶代表我对你的爱，你看看碗里面有什么……”

* * *

早餐是一天中最重要的一餐。每天早上，我都目光呆滞地盯着麦片盒上的配料表，心里默念这句话，等着没睡够的倦意退去。如果你泡了碗麦片，冲了杯咖啡或者倒了杯果汁，那么，在阳光的照耀下，杯子里面会出现一个类似心形的形状（图1.1）。

图 1.1　阳光照射下的碗里出现心形（图片来源：© Gérard Janot, CC BY-SA 3.0）

这个心形是怎么来的呢？

答案其实很简单，但先要了解下数学家是如何定义心形的。

画一颗心给你！

有了合适的方程和绘图仪，什么东西都可以画出来。Wolfram[1]公司市场部的编辑理查德 · 克拉克特别擅于用傅里叶变换写图形方程。有了他的贡献，我们才能把皮卡丘也用方程表示出来（图1.2a）——我在这里就不把方程写全了，如果要写全，一页纸都不够。美国一所高中的数学老师 J. 马修 · 雷吉斯特也是图形方程的好手。2011 年，他的学生把他的蝙蝠侠图标方程（图1.2b）发到了网上，引起了轰动。言归正传，数学爱好者给出了许多心形方程，各有千秋，但数学界“心有独钟”：他们认定用简单方程描绘的“心形线”（图1.2c 和图1.2d）。

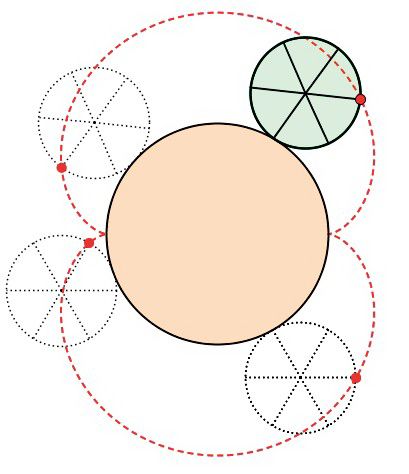
心形线在英语里叫作 cardioid，这个词来自希腊语：kardia 意为“心”，eidos 意为“形”。心形线有许多不同的定义方法，但是异曲同工（图1.2）。我们可以想象一个圆沿着另一个圆外侧滚动而不滑动，不动的圆叫作“准圆”，动圆上某一点的轨迹称为“外摆线”（epicycloid），这个词也来自希腊语：epi 意为“上”，kuklos 意为“圆”。准圆和动圆的半径相等时，就得到了心形线。如果动圆在准圆内部，而准圆的半径是动圆的2倍，也会得到心形线。

18世纪初，布莱兹 · 帕斯卡的父亲艾蒂安 · 帕斯卡在对摆线的研究中提到了这种曲线，虽然言辞含糊，但这是历史上首次出现。其他数学家对这种曲线也是兴致勃勃。1708年，法国数学家菲利普 · 德拉意尔证明心形线的长是准圆半径的16倍。直到1741年，乔瓦尼 · 达卡斯蒂利奥内才根据形状将其命名为“心形线”。

图 1.2　几条有趣的曲线

^{(a) 理查德 · 克拉克的皮卡丘曲线。这是一个参数方程，t 的取值在0到 2π 之间，曲线上某一点的坐标由(x, y)关于 t 的函数确定，即(x(t), y(t))。这里只给出了皮卡丘轮廓线的方程，完整的方程是其10倍长。}

^{(b) J. 马修 · 雷吉斯特的蝙蝠侠图标曲线。起初方程只有一个解析式，以椭圆方程和直线方程为基础。}

^{(c) 尤尔根 · 科勒的心形曲线。}

^{(d) 参数方程给出的心形线。}

第二种构建心形线的方法是：取圆上一点 P，以圆上其他点为圆心，作经过点 P 的圆，所有这些圆内包于一条心形线。

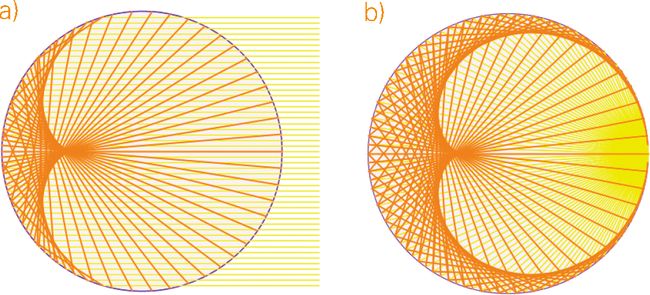
更让人意想不到的是，心形线还可以通过数论的方法来构建。在圆周上均匀地取100个点，编为0到99号，然后把各个点与编号为其2倍的点相连，如果编号的2倍大于等于100，则以减去100计，即编号乘2得100则对应点0，编号乘2得102则对应点2。按这种方法，点21与点42相连，点53与点6相连。所有这些线段形成心形线。取的点越多，心形线就越准确（图1.3）。

图 1.3　构建心形线的几个方法

^{可以是圆的外摆线 (a)，也可以是经过圆周上一点且圆心也在此圆周上的圆的包络线 (b)，或者圆周上某点与其2倍编号点连线的包络线 (c)。}

说了这么多，还没有解释碗里怎么会有一颗“心”。真正原因是，心形线是圆的“散焦线”。

光之几何

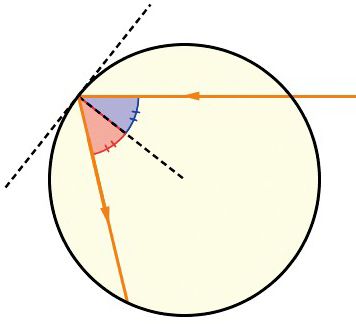
光线照射到圆形容器的边缘，会发生反射。假设阳光是平行光，让我们来观察一下反射光路：根据光的反射定律，反射角等于入射角，即反射光线与法线的夹角等于入射光线与法线的夹角，法线是圆在入射点上切线的垂线（图1.4）。

图 1.4　光在曲线上的反射

^{根据光的反射定律（又称“斯内尔 - 笛卡儿第一定律”），反射角（红色）等于入射角（蓝色）。}

阳光视为平行光，照射到杯沿并经过反射后，汇集成的曲线就是所谓的“散焦线”，与所有反射光路相切。这里的散焦线和心形线很相似（图1.5a）。

图 1.5　(a) 将阳光视为平行光，反射以后形成的“散焦线”与心形线很相似。这其实是另一种外摆线，称为“肾形线”。(b) 当光源位于圆周上的一点时，才能得到心形线

但是，这样得到的曲线并不是真正的心形线，心形线与圆周不会相交。其实，这是半肾形线，可以视为心形线的“亲戚”，因为它们都是外摆线的一种。如果准圆的直径是动圆的2倍，就会得到肾形线（图1.6）。肾形线有两个对称轴和两个回复点，即曲线好像要往回走的那一点。“肾形线”这个词英语为 nephroid，也来自希腊语，nephrós 意为“肾”。这听起来就没“心形线”那么浪漫了。

图 1.6 如果准圆的半径是动圆的2倍，则动圆上某点的轨迹是另一种外摆线，称为“肾形线”

但不要担心，想要杯子里出现心形线很简单，只要把光源移近一点就行。光源在杯子的圆周上时，出现的就是标准的心行线（图1.5b）。下一个情人节，你就可以省着点过啦！不用去高级餐厅吃大餐，只要一盏灯和一碗牛奶就够了，然后再给他或她念一首诗，完美[2]！

* * *

如果你是外摆线，你会是一条心形线。

如果你是全纯函数，你就是正弦的平方，

而我就是余弦的平方，我们刚好合二为一。

如果你是偶数，你会是28，因为28是完全数。

如果你是奇数，你依然会是完全数。

但只有我知道，你这个奇完全数的存在。

如果你是对数，你将会……那个……你懂的。

---

[1] Wolfram Research 是一家美国公司，主攻数学领域，其产品 Mathematica 是一种科学计算软件，其开发的网站 Wolfram| Alpha 是一种计算搜索引擎。

[2] 如果你真的这么做了，但你的心上人并不领情，作者不承担任何责任。

02　照（不）亮你的家

03　瓷砖铺法知多少

04　青梅竹马分披萨

05　如何平分有菠萝、奇异果和樱桃的蛋糕

06　创意桌上游戏

07　挂不上墙的神作

08　认识地球的形状

09　认识宇宙的形状

10　教你数数

11　争霸法国网球公开赛

12　你究竟有几个冷笑话

13　玩转《地产大亨》

14　如何选秘书

15　山无陵，天地合，乃敢与君绝

16　议会席位怎么分？

17　如何选总统？

18　走出迷宫

19　盖茨翻煎饼

20　小便器优选法

参考文献

阅读全文: http://gitbook.cn/gitchat/geekbook/5b7a42c49a18602b5bc07a14