十大经典算法之Apriori

数据挖掘十大经典算法：KNN、C4.5、Naive Bayes、CART、SVM、Kmeans、PageRank、AdaBoost、EM、Apriori

---

前言：部分参考的博客已标出

关联规则简介

关联规则分析：目的是在一个数据集中找出各项之间的关联关系，而这种关系在数据集中并不能直观表现出来。

购物篮分析就是关联规则一个著名应用：例如，一个超市的经理想更多了解顾客的购物习惯，比如”哪组商品在一次购买中同时购买“或”某顾客购买了个人电脑，那么该顾客三个月后购买数码相机的概率多大“。若发现顾客如果购买了面包同时非常有可能购买牛奶，那么道出了一条关联规则“面包 ==> 牛奶”。其中面包未规则前项，而牛奶未后项，通过对面包降低销售价进行促销，而适当提高牛奶的售价，关联销售出的牛奶旧可能增加超市整体的利润。

国内外应用1

就目前而言，关联规则挖掘技术已经被广泛应用在西方金融行业企业中，它可以成功预测银行客户需求。一旦获得了这些信息，银行就可以改善自身营销。现在银行天天都在开发新的沟通客户的方法。各银行在自己的ATM机上就捆绑了顾客可能感兴趣的本行产品信息，供使用本行ATM机的用户了解。如果数据库中显示，某个高信用限额的客户更换了地址，这个客户很有可能新近购买了一栋更大的住宅，因此会有可能需要更高信用限额，更高端的新信用卡，或者需要一个住房改善贷款，这些产品都可以通过信用卡账单邮寄给客户。当客户打电话咨询的时候，数据库可以有力地帮助电话销售代表。销售代表的电脑屏幕上可以显示出客户的特点，同时也可以显示出顾客会对什么产品感兴趣。

其中我们众所周知的例子如：2
(1) 沃尔玛超市的尿布与啤酒
(2) 超市的牛奶与面包
(3) 百度文库推荐相关文档
(4) 淘宝推荐相关书籍
(5) 医疗推荐可能的治疗组合
(6) 银行推荐相关联业务
这些都是商务智能和关联规则在实际生活中的运用。

但是目前在我国，“数据海量，信息缺乏”是商业银行在数据大集中之后普遍所面对的尴尬。目前金融业实施的大多数数据库只能实现数据的录入、查询、统计等较低层次的功能，却无法发现数据中存在的各种有用的信息，譬如对这些数据进行分析，发现其数据模式及特征，然后可能发现某个客户、消费群体或组织的金融和商业兴趣，并可观察金融市场的变化趋势。可以说，关联规则挖掘的技术在我国的研究与应用并不是很广泛深入。

近年研究1

由于许多应用问题往往比超市购买问题更复杂，大量研究从不同的角度对关联规则做了扩展，将更多的因素集成到关联规则挖掘方法之中，以此丰富关联规则的应用领域，拓宽支持管理决策的范围。如考虑属性之间的类别层次关系，时态关系，多表挖掘等。近年来围绕关联规则的研究主要集中于两个方面，即扩展经典关联规则能够解决问题的范围，改善经典关联规则挖掘算法效率和规则兴趣性。

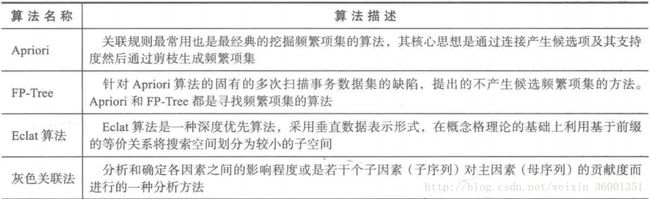
常用关联规则算法

Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。很多的的挖掘算法是在Apriori算法的基础上进行改进的，比如基于散列（Hash）的方法，基于数据分割（Partition）的方法以及不产生候选项集的FP-GROWTH方法等。因此要了解关联规则算法不得不先要了解Apriori算法

Apriori算法

现实中，一销售为例：提取关联规则最大困难：商品类别多，导致可能的商品组合数目会很多。各种关联规则算法的目标：从不同方面入手，以减少可能的搜索空间大小及减少扫描数据的次数。

Apriori算法：最经典的挖掘频繁项集算法，第一次实现了在大数据集上可行的关联规则提取，核心思想：通过连接产生候选项与其支持度，然后通过剪枝生成频繁项集。

关联规则和频繁项集

• 关联规则一般形式：
  项集A、B同时发生的概率为关联规则的支持度（相对支持度）
  
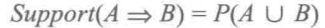
  项集A发生、则项集B发生的概率为关联规则的置信度
  
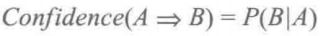
• 最小支持度和最小置信度
  最小支持度：用户或者专家定义的衡量支持度的一个阀值，表示项目集在统计意义上的最低重要性；
  最小置信度：用户或专家定义的衡量置信度的一个阀值，表示关联规则的最低可靠性。
  同时满足最小支持度阀值核最小置信度阀值的规则称强规则
• 项集
  项的集合，包含K个项的项集称K项集：例集合{牛奶，麦片，糖}是一个3项集
  项集的出现概率是所有包含项集的事务计数，称为绝对支持度(支持度计数)。
  频繁项集：若项集I相对支持度满足预定义的最小支持度阀值，则I是频繁项集，频繁K项集记作K
• 支持度计数
  已知支持度计算，则规则A==>B的支持度核置信度可从所有事务计数、项集A和项集A∪B的支持度计数：ps：图片中支持度应该为P(B/A)表示A发生前提下B发生的概率
  
  以上知：输入：所有事务个数、A、B、和A∩B的支持度计数
  输出：关联规则A==>B和B==>A
  置信度公式：分子是包含项集A∩B事务数，分母为项集A的事务数

Apriori算法流程

性质：
频繁项集（支持度必须大于等于给定的最小支持度阀值）的所有非空子集也必须是频繁项集
当非频繁项集I的项集中添加事务A，新的项集I∪A一定不是频繁项集
* 实现流程
1. 找出所有频繁项集，过程由连接步核剪枝步互相融合，获得最大频繁项集Lk
- 连接步
目的：找出K项集。
（1） 对给定的最小支持度阀值，分别对1项候选集C1，剔除小于改阀值的项集得到1项频繁集L1;
（2）L1自身连接产生2项候选集C2，保留C2中满足约束条件的项集得到2项集L2；
（3）L2与L1连接产生3项候选集C3，保留C3中满足约束条件的项集L3
（4）循环下去，得到最大频繁项集Lk
- 剪枝步
紧接着连接步，在产生候选项Ck过程中起到减小搜索空间目的
Ck是Lk-1与L1连接产生，根据Apriori性质，不满足的项集不会存在Ck中，即剪枝
2. 由频发项集产生强关联规则，由1获得满足最小置信度阀值频繁项集，因此挖掘出了强关联规则

实现实例

下面结合举一个实例，使得更能理解算法过程。
数据库中部分点餐数据：

上表为事务数据，整理称关联规则模型所需数据结构：事务数据集
假设：事务数据集为10个点餐订单，设定支持度S=0.2（支持度计数2），菜品{18491,8842,8693,7794,8705}记为{a,b,c,d,e}

过程：

• 找最大K项频繁集
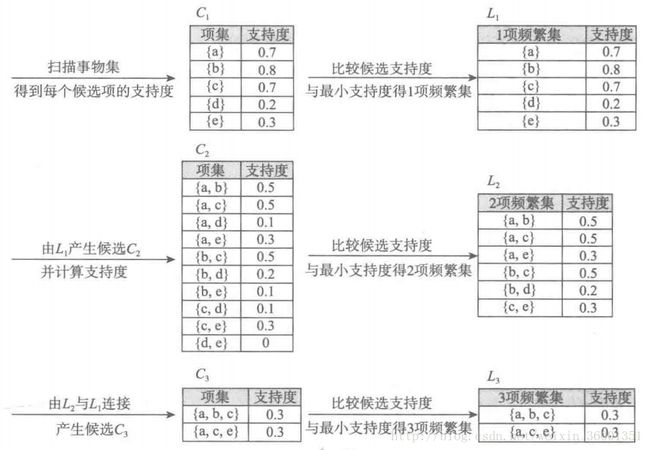
  1） 总共有10个事务，事务中每一项都是候选1项集合C1的成员，计算每一项支持度：P（{a}）=项集{a}支持度计数/所有事务个数=7/10=0.7；对C1中各项支持度与设定支持度S比较，得1项频繁集L1,如上图第一行。
  2）扫描所有事务，L1与L1连接得到候选2项集C2，计算每一项的支持度：P({a,b})=项集{a,b}支持度个数/所有事务个数=5/10=0.5，然后剪枝步：C2中每个自己L1都是频繁集，没有项集从C2中剔除
  3） 对C2中各项集支持度与预设S比较，得到L2如上图
  4）扫描所有事务，L2与L1连接得到候选3项集C3，并计算每一项支持度：P({a,b,c})=项集{a,b,c}支持度计数/所有事务个数=3/10=0.3，接下来剪枝：L2和L1连接的所有项集：{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,c,e},{b,c,d},{b,c,e}。根据Apriori算法性质，因为{b,d},{b,e},{c,d}不在L2中，剔除。最后C3中项集为{a,b,c},{a,c,e}
  5）对C3求各项支持度，过滤，得到3项频繁集L3
  6）L3与L1连接得到候选集4项，剪枝后为空。终止。
  最后结果：L1、L2、L3都是频繁项集，L2是最大频繁项集
• 频繁集产生关联规则
  根据置信度公式，产生关联规则：
  

第一条：客户在点了菜品a和b的概率是50%，点了菜品a，再点了b的概率是71.428%

优缺点

• 算法优点： 简单、易理解、数据要求低

• 算法缺点： I/O负载大，产生过多的候选项目集

• 应用领域： 消费市场价格分析，入侵检测，移动通信领域

代码实现

将Apriori算法用于实际数据。不给数据集的都是耍流氓：kosarak.dat
数据集：新闻网站点击流的数据集，每一行包含某个用户浏览过的新闻报道，新闻报道被编码成整数(新闻ID)，总共有99万条。
一个样本：一个用户浏览过的所有新闻ID，用空格隔开

目的：挖掘热门新闻报道，使用Apriori或FP-growth算法挖掘其中的频繁项集，查看那些新闻ID被用户大量观看到
代码包：

算法	python	Java	R	pyspark
apriori	无包	weka.associations.Apriori	arules包	无包

人工实现：
python: 大神博客
pyspark：大神博客

待找python中相关包~~~

FP-growth高效算法

参考书籍：
Python数据分析与挖掘实战_张良均
[1] http://www.36dsj.com/archives/2443
优秀博客： http://www.cnblogs.com/qwertWZ/p/4510857.html
[2] http://blog.csdn.net/eastmount/article/details/53368440