【VIO笔记（学习VINS的必备基础）】第七讲 VINS系统构建

系列教程来自某学院，侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力，不然直接撸网上的各种VINS解析完全云里雾里-_-!

这一讲是本系列的最后一讲，我们会对之前的内容进行一个回顾，并对VINS系统进行研究。

VIO基础回顾

IMU基础回顾

预积分的作用是为了避免世界坐标系和body系下的变换，如上图中红色的表示预积分值，而每个小黑点代表一个IMU测量，通过预积分就可以约束两帧图像之间的变换，IMU的传感器模型如下：

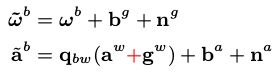
预积分的公式如下：

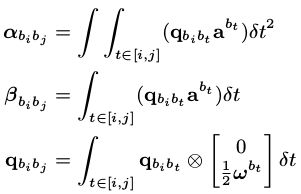
另外还有一点是IMU的协方差传递，由于每一个小黑点测量时都有一个测量误差，那么我们后来运用的预计分量也就存在误差，那么一段时间内多个误差的传递就要用到协方差的传递，最后用来估计预积分的不确定度。

视觉基础回顾

这部分在第六讲刚刚讲过，主要在视觉部分如何获取相机的变换。

1. 对于两帧图像，我们要先进行特征点的提取和匹配。
2. 已知俩图像特征匹配点:利用对极几何约束 (E 矩阵,H 矩阵),计算两图像之间的 pose。
3. 已知相机pose后，通过三角化获取特征点的三维坐标。
4. 此时当新来一帧图像时，由于共视关系会出现已知3d点和2d特征点的情况，此时我们使用PnP来求新相机的pose。

在纯视觉的vSlam中，前三步就完成了相机的初始化，但是此时我们是在系统内部形成了尺度，并不知道系统在实际3D空间中的米制信息。

问题探讨

上图就是一个VIO系统，在我们了解了视觉和IMU分别是如何工作之后，我们还需要考虑一些问题：

1. IMU 怎么和世界坐标系对齐,计算初始时刻的 $q_{w{b}_0}$?
2. 单目视觉姿态如何和 IMU 轨迹对齐,尺度如何获取?
3. VIO 系统的初始速度 v,传感器 bias 等如何估计?
4. IMU 和相机之间的外参数等

这就是VIO系统初始化时需要考虑的一些问题，下面我们一一来进行分析。

VINS初始化

视觉和IMU之间存在着一定的联系，利用这些几何的约束，我们就可以进行初始化，对于下面这幅图：

使用外参数$q_{bc}$、$t_{bc}$可以获得下面两个式子，记为式3，第一行表示从bk位置变换到c0位置的旋转变换，第二行中s表示尺度因子，带bar的p：$\bar{p}$表示非米制单位下，也就是系统内部的单位下的位移，第二行的式子就表示bk到c0的位置变换。

对第二行的式子进行变换可以得到非米制单位下ck到c0的位置变换：

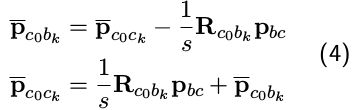
这几个量会在后面的公式推到中用到。下面我们先对视觉 IMU 对齐流程做一个梳理：

1. 旋转外参数 $q_{bc}$ 未知, 则先估计旋转外参数。
2. 利用旋转约束估计陀螺仪 bias，旋转约束就是式3的第一行。
3. 利用平移约束估计重力方向,速度,以及尺度初始值，平移约束就是式3的第二行。
4. 对重力向量 $g^{c_0}$ 进行进一步优化
5. 求解世界坐标系 w 和初始相机坐标系 c0 之间的旋转矩阵 $q_{w{c}_0}$ ,并将轨迹对齐到世界坐标系。

利用旋转约束估计外参数旋转$q_{bc}$

$q_{bc}$是相机系和body系的旋转矩阵，当然还有它对应的平移矩阵$p_{bc}$，但是这个矩阵通常就是几厘米的位移或者是固定在已知标定板上的，所以重点需要估计的是旋转矩阵，这个平移矩阵通常默认为已知值。
在相邻两个视觉帧下，我们可以通过两条路径从$b_{k+1}$到$c_k$，分别是先换到$b_k$再右乘$q_{bc}$到$c_k$（对应等式左边），或者先换到$c_{k+1}$再右乘相机系下的旋转到$c_k$：

将上式挪到一边，并将左乘右乘写到一起，得到：

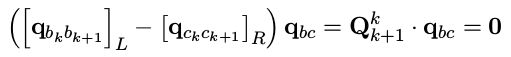
我们将多个时刻的方程累计起来，并加上鲁棒核权重得到：

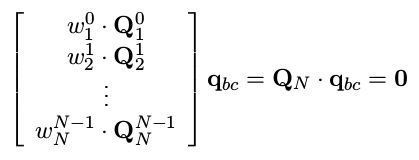
这里就得到一个Ax=0的方程，利用上节课求三角化的时候解方程的结论，此时的$q_{bc}$的解就是$Q_N$的特征值分解后最小的特征向量，这里鲁棒核权重取：

其中

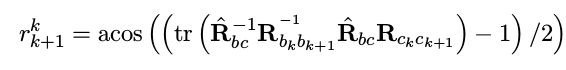
它表示的是旋转的轴角角度误差，由公式$tr(R)=1+2cos\theta$可以得到，上式中的四个旋转相乘后应该旋转角度为0，那么如果r计算出来很大则说明该次计算结果出现了误差，就应该给它一个小的权重。另外在VINS中还有一个trick就是当$Q_N$SVD分解后的特征向量很小时，就说明这次估计无效，会重新估计。

基于旋转约束估计Bias

在$q_{bc}$已经标定好的情况下，利用旋转约束可以得到：

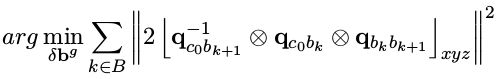
其中$q_{c_0{b}_{k+1}}$和$q_{c_0{b}_k}$都是由视觉和已知的$q_{bc}$计算得到，可以认为是比较准确的值，而后面的$q_{b_k{b}_{k+1}}$是有IMU积分得到的，存在bias，将其进行一阶泰勒展开：

带hat的q和相机得到的q相乘理论上是一个单位阵，那么整个最小二乘最后就只有$J_{b^g}^q\delta b^g$（1/2被消掉），构建Hx=b即可求解。

初始化速度、重力和尺度因子

在这一部分需要估计的变量有body系下n个时刻的速度v，相机系下的重力加速度g，尺度因子s：

通过世界坐标系下的预积分约束我们可以得到：

将其转换到相机坐标系下得到下式，其中就有$g^{c_0}$、$v_k^{b_k}$、s：

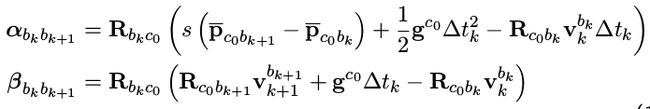
将之前的公式3带入上式，将其中的p转换为相机坐标系下的。

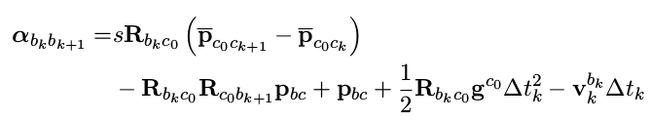
我们将带pbc的项移到等式左边，待估计的量放在等式右边，这样可以把$\alpha$和$\beta$写成下面的矩阵形式，方便我们后面进行最小二乘优化：

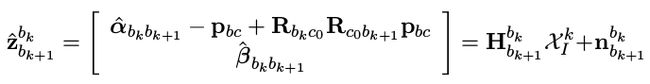
其中：

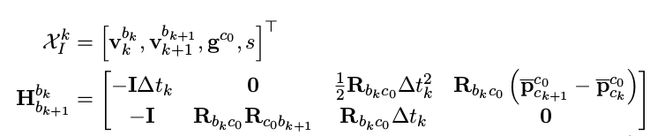
这样就构建了一个等式，我们就可以将其写成最小二乘的形式进行求解：

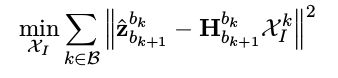
优化重力向量 $g^{c_0}$

由于在上面优化g时没有引入模长9.81的限制，因此估计出的g只有两个自由度，不够准确，之后还要用到重力向量来估计旋转，所以需要对g进行优化，三维向量只有2个自由度时可以采用球面坐标进行参数化：

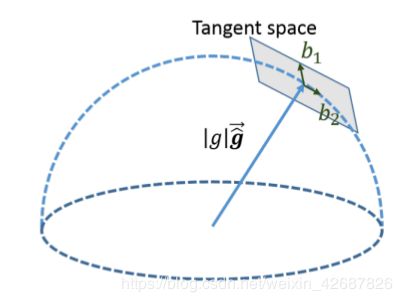
将其表示成如下的式子，带hat的g表示单位向量，乘上模长就是上图的蓝色箭头表示上一步估计出来的g，然后w1和w2为待优化的变量。

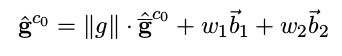
其中

展开了一个球的切面，将新的g带入回上一步的待估计变量矩阵中：


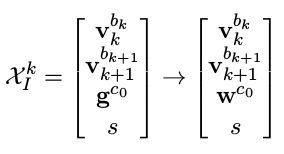
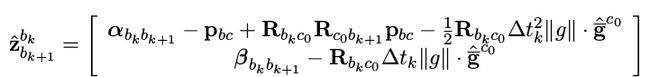
利用最小二乘再进行优化。

将相机坐标系对齐世界坐标系

完成了前面四步，我们可以将两个坐标系对齐，就完成了系统的初始化：

1. 找到 c0 到 w 系的旋转矩阵
   
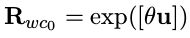
   其中
   
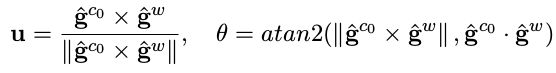
   该矩阵是通过两个坐标系下重力向量的对比得到的，由于重力加速度是相同的，因此可以通过其计算出旋转矩阵R。
2. 把所有 c0 坐标系下的变量旋转到 w 下
3. 把相机平移和特征点尺度恢复到米制单位

初始化完成！

VINS 系统

终于到了这个课程的最后一章，回忆之前的所学，基本涉及到了VINS系统的各个部分。VINS系统可以分为三大块：
1 前端,数据处理:特征提取匹配,imu 积分
2 初始化:系统初始状态变量(重力方向,速度,尺度等等)
3 后端:滑动窗口优化

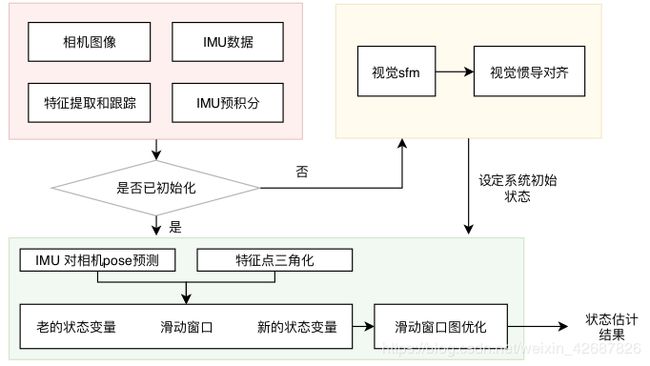
后端的滑动窗口的优化的状态变量我们再回顾一下：

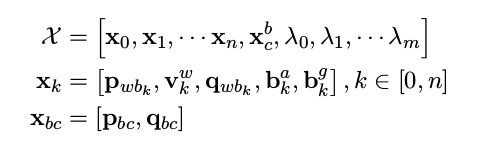
xk是每个时刻的pose、速度、旋转、偏置，$\lambda$是路标点的逆深度，xbc是外参数。最后要优化的整个残差项为：

结语

终于结束了这门课程的学习，当然很多知识不是学习一遍就能够全部掌握的，所以之后我会利用VINS的论文和源码再进行一次巩固和查漏补缺，同时VINS作为基于优化的VIO系统，自然就有基于滤波的VIO系统，这都是之后学习的方向。总之前路漫漫，同志仍需努力。