方差、协方差、相关系数的理解
方差和协方差机器学习中常见的两个概念,公式也几乎是随处可见,但是每见一次都像是初次见面,又去想半天各种公式、概念和意义,所以下定决心整理一下。
方差和协方差
定义
方差
度量单个随机变量的离散程度,公式如下:
σ x 2 = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) 2 \sigma^2_x = \frac{1}{n-1}\sum_{i=1}^n(x_i-\overline{x})^2 σx2=n−11i=1∑n(xi−x)2
协方差
度量两个随机变量(变化趋势)的相似程度,定义如下:
σ ( x , y ) = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) ( y i − y ‾ ) \sigma(x,y)= \frac{1}{n-1}\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y}) σ(x,y)=n−11i=1∑n(xi−x)(yi−y)
C o v ( X , Y ) = E [ ( X − μ x ) ( Y − μ y ) ] Cov(X,Y) = E[(X-\mu_x)(Y-\mu_y)] Cov(X,Y)=E[(X−μx)(Y−μy)]
以上两个公式就可以看出,方差和协方差的定义同宗。
图解
那么方差是怎么衡量随机变量的离散程度的呢?协方差又怎么衡量变量的变化趋势的呢?
方差
图1
离散程度具体来说衡量的是随机变量偏离均值的幅度大小,单个数据点x的偏离幅度为x与x均值的距离平方和。
上图中的右上图和右下图,两个随机变量的均值虽然都为0,但是很明显右下图中随机变量偏离均值的幅度更大,各自的方差为:
( 2 ∗ ( 70 − 0 ) 2 + 2 ∗ ( − 70 − 0 ) 2 + ( − 200 − 0 ) 2 + ( 200 − 0 ) 2 ) = 99600 (2*(70-0)^2+2*(-70-0)^2+(-200-0)^2+(200-0)^2)=99600 (2∗(70−0)2+2∗(−70−0)2+(−200−0)2+(200−0)2)=99600
( 2 ∗ ( 0.01 − 0 ) 2 + 2 ∗ ( − 0.01 − 0 ) 2 + ( − 0.02 − 0 ) 2 + ( 0.02 − 0 ) 2 ) = 0.001 (2*(0.01-0)^2+2*(-0.01-0)^2+(-0.02-0)^2+(0.02-0)^2)=0.001 (2∗(0.01−0)2+2∗(−0.01−0)2+(−0.02−0)2+(0.02−0)2)=0.001
所以右上图的离散变量分布的更紧凑。
协方差
对于变量X、Y,协方差的定义为每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”的均值(其实是求“期望”)。因此,如果x与x的均值差与y与y的均值差的符号相同,则协方差值大于0,符号相反,则协方差值小于0,总结如下:

图2

图3

图4
在图2、3、4中的区域(1)中,有 X>EX ,Y-EY>0 ,所以(X-EX)(Y-EY)>0;
在图2、3、4中的区域(2)中,有 X
在图2、3、4中的区域(3)中,有 X
在图2、3、4中的区域(4)中,有 X>EX ,Y-EY<0 ,所以(X-EX)(Y-EY)<0。
当X 与Y 正相关时,它们的分布大部分在区域(1)和(3)中,小部分在区域(2)和(4)中,所以平均来说,有E(X-EX)(Y-EY)>0 。
当 X与 Y负相关时,它们的分布大部分在区域(2)和(4)中,小部分在区域(1)和(3)中,所以平均来说,有(X-EX)(Y-EY)<0 。
当 X与 Y不相关时,它们在区域(1)和(3)中的分布,与在区域(2)和(4)中的分布几乎一样多,所以平均来说,有(X-EX)(Y-EY)=0 。
所以,我们可以定义一个表示X, Y 相互关系的数字特征,也就是协方差
cov(X, Y) = E(X-EX)(Y-EY)。
当 cov(X, Y)>0时,表明 X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
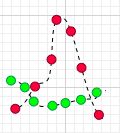
而大多数情况下,变量X,Y的变化趋势不会像图一一样严格的同增大同减小,大多如图5和图6一样,这时只要求期望就可以了。
相关系数
由协方差的概念相关系数,其定义如下:
ρ = C o v ( X , Y ) σ X σ Y \rho = \frac{Cov(X,Y)}{\sigma_X\sigma_Y} ρ=σXσYCov(X,Y)
就是用X、Y的协方差除以X的标准差和Y的标准差。
在图一中,情况一和情况二的协方差计算如下:
情况一
[ ( 100 − 0 ) × ( 70 − 0 ) + ( − 100 − 0 ) × ( − 70 − 0 ) + ( − 200 − 0 ) × ( − 200 − 0 ) . . . ] ÷ 7 ≈ 15428.57 [(100-0)\times(70-0)+(-100-0)\times(-70-0)+(-200-0)\times(-200-0)...]\div7\approx 15428.57 [(100−0)×(70−0)+(−100−0)×(−70−0)+(−200−0)×(−200−0)...]÷7≈15428.57
情况二:
[ ( 0.01 − 0 ) × ( 70 − 0 ) + ( − 0.01 − 0 ) × ( − 70 − 0 ) + ( − 0.02 − 0 ) × ( − 200 − 0 ) . . . ] ÷ 7 ≈ 1.542857 [(0.01-0)\times(70-0)+(-0.01-0)\times(-70-0)+(-0.02-0)\times(-200-0)...]\div7\approx 1.542857 [(0.01−0)×(70−0)+(−0.01−0)×(−70−0)+(−0.02−0)×(−200−0)...]÷7≈1.542857
由以上计算可知,除了协方差的正负号表示变量的变化趋势是否一致之外,数值的大小还表示变化相似的程度,而相关系数则是协方差的标准化,两种情况的相关系数如下:
情况一:
ρ 1 = 15428.57 ÷ ( 130.9307 × 119.2836 ) ≈ 0.9879 \rho_1 = 15428.57 \div (130.9307 \times 119.2836) \approx 0.9879 ρ1=15428.57÷(130.9307×119.2836)≈0.9879
情况二:
ρ 2 = 1.542857 ÷ ( 0.01309307 × 119.2836 ) ≈ 0.9879 \rho_2 = 1.542857 \div (0.01309307 \times 119.2836) \approx 0.9879 ρ2=1.542857÷(0.01309307×119.2836)≈0.9879
因此相关系数:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
参考:
如何通俗易懂地解释「协方差」与「相关系数」的概念? - GRAYLAMB的回答 - 知乎
https://www.zhihu.com/question/20852004/answer/134902061
终于明白协方差的意义了