codeforces 1234C Pipes

C. Pipes

input

standard input

output

standard output

You are given a system of pipes. It consists of two rows, each row consists of n pipes. The top left pipe has the coordinates (1,1) and the bottom right — (2,n).

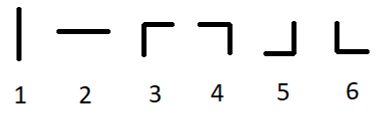
There are six types of pipes: two types of straight pipes and four types of curved pipes. Here are the examples of all six types:

                               

                                                                         Types of pipes

You can turn each of the given pipes 90 degrees clockwise or counterclockwise arbitrary (possibly, zero) number of times (so the types 1 and 2 can become each other and types 3,4,5,6 can become each other).

You want to turn some pipes in a way that the water flow can start at (1,0) (to the left of the top left pipe), move to the pipe at (1,1), flow somehow by connected pipes to the pipe at (2,n) and flow right to (2,n+1)

.

Pipes are connected if they are adjacent in the system and their ends are connected. Here are examples of connected pipes:

                                         

Examples of connected pipes

Let's describe the problem using some example:

                 

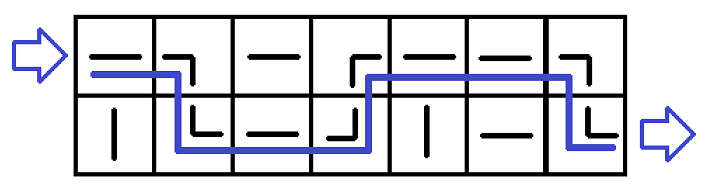
The first example input

And its solution is below:

                 

The first example answer

As you can see, the water flow is the poorly drawn blue line. To obtain the answer, we need to turn the pipe at (1,2)

90 degrees clockwise, the pipe at (2,3) 90 degrees, the pipe at (1,6) 90 degrees, the pipe at (1,7) 180 degrees and the pipe at (2,7) 180 degrees. Then the flow of water can reach (2,n+1) from (1,0)

.

You have to answer qindependent queries.

Input

The first line of the input contains one integer q (1≤q≤104) — the number of queries. Then qqueries follow.

Each query consists of exactly three lines. The first line of the query contains one integer n

(1≤n≤2⋅105) — the number of pipes in each row. The next two lines contain a description of the first and the second rows correspondingly. Each row description consists of n digits from 1 to 6without any whitespaces between them, each digit corresponds to the type of pipe in the corresponding cell. See the problem statement to understand which digits correspond to which types of pipes.

It is guaranteed that the sum of nover all queries does not exceed 2⋅105

.

Output

For the i-th query print the answer for it — "YES" (without quotes) if it is possible to turn some pipes in a way that the water flow can reach (2,n+1) from (1,0), and "NO" otherwise.

Example

Input

Copy

6
7
2323216
1615124
1
3
4
2
13
24
2
12
34
3
536
345
2
46
54

Output

Copy

YES
YES
YES
NO
YES
NO

Note

The first query from the example is described in the problem statement.

 

像走迷宫一样的，可以直接dfs，虽然管子的种类有六种，但其实仔细分析一下，只有两种，1，2和3，4，5，6

每种管子都有着确定的流向

详细解释看代码中的注释

#include
using namespace std;
const int maxn = 2e5+100;
bool flag = 0;
char tubes[2][maxn];
int length, n;
void dfs(int x, int y, int way) {//way表示x,y这个点将要流向哪一个方向
	if (y >= length)
		return;
	if (x == 1 && y == length -1 && way == 3) {
		flag = 1;
		return;
	}
	if (x == 0) {//现在在第一行,下一步只能向右或向下
		if (way == 3)//向右流
		{
			if (tubes[x][y+1] == '1' || tubes[x][y+1] == '2') {
				dfs(x, y + 1, 3);
			}
			else {
				dfs(x, y + 1, 2);
			}
		}
		else if (way == 2)//向下流
		{
			if (tubes[x + 1][y] != '1' && tubes[x + 1][y] != '2') {
				dfs(x + 1, y, 3);
			}
		}
	}
	else if (x == 1) {//在第二行，下一步只能向上或向右
		if (way == 3) {
			if (tubes[x][y+1] != '1'&& tubes[x][y+1] != '2') {
				dfs(x, y + 1, 1);
			}
			else dfs(x, y + 1, 3);
		}
		else if (way == 1) {
			if (tubes[x - 1][y] != '1' && tubes[x - 1][y]!= '2') {
				dfs(x - 1, y, 3);
			}
		}
	}
}

int main() {//1向上走2向下走3向右走
	cin >> n;
	while (n--) {
		flag = 0;
		cin >> length;
		cin >> tubes[0];
		cin >> tubes[1];
		if (tubes[0][0] == '1' || tubes[0][0] == '2')//向右走
			dfs(0, 0, 3);
		else
			dfs(0, 0, 2);//向下走
		if (flag)
			cout << "YES" << endl;
		else
			cout << "NO" << endl;
	}
	//system("pause");
	return 0;
}