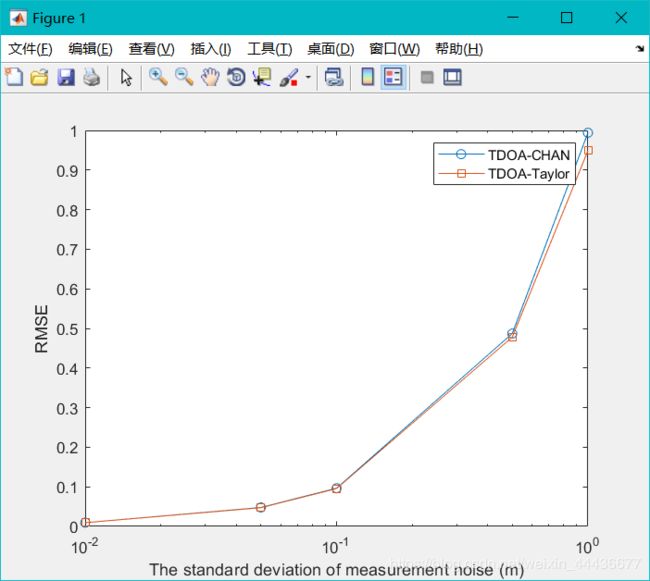
Matlab-TDOA定位算法性能仿真 TDOA-CHAN和TDOA-Taylor得到位置的估计 两种算法的性能比较 两种算法的RMSE曲线对比图
本博客环境为Matlab2018 ,软件版本不同可能会有些出入,需要稍作修改。
TDOA定位算法性能的仿真
要求一:编写两个函数TDOA_CHAN和TDOA_Taylor得到位置的估计。
要求二:用RMSE实现两种算法的性能比较, 得到两种算法的RMSE曲线对比图,横坐标为噪声方差,纵坐标为RMSE。
主函数:
我的文件命名为TDOA.m
%the simulation of TDOA localization algorithm
clear all;
clc;
%定义四个参与基站的坐标位置
BS1=[0,0];BS2=[500,0];BS3=[500,500];BS4=[0,500];
MS=[50,100]; %移动台MS的初始估计位置
std_var=[1e-2,5e-2,1e-1,5e-1,1]; %范围
A=[BS1;BS2;BS3;BS4];%矩阵A包含4个初始坐标
number=10000;
for j=1:length(std_var)%循环
error1=0;error2=0;%初始误差置为0
std_var1=std_var(j);%令std_var1等于当前数组的值
for i=1:number %多次循环
r1=A-ones(4,1)*MS;
r2=(sum(r1.^2,2)).^(1/2);
r=r2(2:end,:)-ones(3,1)*r2(1,:)+std_var1*randn(3,1);
sigma=std_var1^2;
theta1=TDOA_CHAN(A,r,sigma); %调用TDOACHAN函数
theta2=TDOA_Taylor(A,r,sigma); %调用TDOATaylor函数
error1=error1+norm(MS-theta1)^2;%移动台MS估计位置与计算的到的距离的平方
error2=error2+norm(MS-theta2)^2;
end
RMSE1(j)=(error1/number)^(1/2);%均方根误差
RMSE2(j)=(error2/number)^(1/2);
end
% plot
semilogx(std_var,RMSE1,'-O',std_var,RMSE2,'-s')% x轴取对数,X轴范围是1e-2到1,Y轴的范围是变动的
xlabel('The standard deviation of measurement noise (m)');
ylabel('RMSE');
legend('TDOA-CHAN','TDOA-Taylor');
TDOA_CHAN函数:
我的文件命名为TDOA_CHAN.m
%TDOA_CHAN
function theta=TDOA_CHAN(A,p,sigma)
% A is the coordinate of BSs A是BSS的坐标
% p is the range measurement P是范围测量
% sigma is the the variance of TOA measurement sigma是TDOA测量的方差
[m,~]=size(A);%size得到A的行列数赋值给[m,~],~表示占位,就是只要行m的值
k=sum(A.^2,2);%矩阵A每个元素分别平方,得到新矩阵,在行求和,最为矩阵K
G1=[A(2:end,:)-ones(m-1,1)*A(1,:),p];%得到Xm1,Ym1,Rm1,的值,m取值[2,i],构建矩阵Ga
h1=1/2*(p.^2-k(2:end,:)+ones(m-1,1)*k(1,:));%构建矩阵h
Q=diag(ones(m-1,1)*sigma);%构建TDOA的协方差矩阵
% initial estimate
theta0=inv(G1'*inv(Q)*G1)*G1'*inv(Q)*h1;%通过一次WLS算法进行求解
s=A(2:end,:)-ones(m-1,1)*theta0(1:2,:)';
d=sum(s.^2,2);%矩阵s每个元素分别平方,得到新矩阵,在行求和,最为矩阵d
B1=diag(d.^(1/2));
cov1=B1*Q*B1;
% first wls
theta1=inv(G1'*inv(cov1)*G1)*G1'*inv(cov1)*h1;%进行第一次WLS计算
cov_theta1=inv(G1'*inv(cov1)*G1);%得到theta1的协方差矩阵
% second wls
G2=[1,0;0,1;1,1];%构建G'
h2=[(theta1(1,1)-A(1,1))^2;(theta1(2,1)-A(1,2))^2;theta1(3,1)^2];%构建h'
B2=diag([theta1(1,1)-A(1,1),theta1(2,1)-A(1,2),theta1(3,1)]);%构建b'
cov2=4*B2*cov_theta1*B2;%得到误差矢量的协方差矩阵
theta2=inv(G2'*inv(cov2)*G2)*G2'*inv(cov2)*h2;%运用最大似然估计得到
theta=theta2.^(1/2)+[A(1,1);A(1,2)];%得到MS位置的估计值坐标,以及符号
theta=theta';%转换为(x,y)形式
TDOA_Taylor函数:
我的文件命名为TDOA_Taylor.m
%TDOA_Taylor
function theta=TDOA_Taylor(A,p,sigma)
% A is the coordinate of BSs
% p is the range measurement
% sigma is the the variance of TOA measurement
% initial estimate
theta0=TDOA_CHAN(A,p,sigma);%调用TDOACHAN得到一个初始的估计位置
delta=norm(theta0);%得到范数
while norm(delta)>1e-2 %得到足够小的值
[m,~]=size(A);%size得到A的行列数赋值给[m,~],~表示占位,就是只要行m的值
d=sum((A-ones(m,1)*theta0).^2,2);
R=d.^(1/2);
G1=ones(m-1,1)*(A(1,1)-theta0(1,1))/R(1,1)-(A(2:m,1)-theta0(1,1))./R(2:m,:);
G2=ones(m-1,1)*(A(1,2)-theta0(1,2))/R(1,1)-(A(2:m,2)-theta0(1,2))./R(2:m,:);
G=[G1,G2];%构建Gt
h=p-(R(2:m,:)-ones(m-1,1)*R(1,:));%构建Ht
Q=diag(ones(m-1,1)*sigma);%TDOA测量值的协方差矩阵
delta=inv(G'*inv(Q)*G)*G'*inv(Q)*h;%加权最小二乘解
theta0=theta0+delta';%累加
end
theta=theta0;