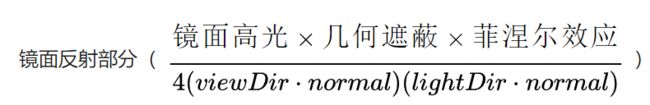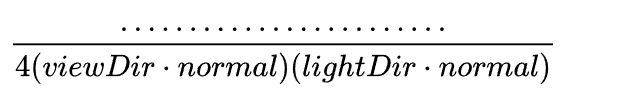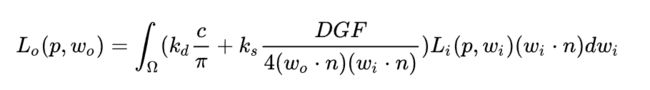关于BRDF的一些总结——转自其他博客
https://blog.csdn.net/poem_qianmo/article/details/100652463
https://www.cnblogs.com/jerrycg/p/4932031.html
1、几何函数和法线分布函数的联系
几何函数和法线分布函数作为microfacet specular BRDF中的重要两项,两者之间具有紧密的联系:
- 几何函数的解析形式依赖于法线分布函数。
- 法线分布函数需要结合几何函数,得到有效的法线分布强度。
单纯的法线分布函数输出值并不是能产生有效反射的法线强度,因为光线的入射和出射会被微平面部分遮挡,即并不是所有朝向m=h的微表面,能在给定光照方向l和观察方向v时可以顺利完成有效的反射。几何函数即是能对顺利完成入射和出射的微平面概率进行建模的函数。
2、几何函数的两种主要形式:G1和G2
- G1为微平面在单个方向(光照方向l和观察方向v)上可见比例,一般代表遮蔽函数(masking function)或阴影函数(shadowing function)
- G2为微平面在光照方向l和观察方向v两个方向上可见比例,一般代表联合遮蔽函数(joint masking-shadowing function)
- 在实践中G2由G1推导而来
- 默认情况下,microfacet BRDF中使用的几何函数代指G2

图 几何函数的两种主要形式:G1和G2。G1为微平面在单个方向(光照方向L或观察方向V)上可见比例。G2为微平面在光照方向L和观察方向V两个方向上可见比例(图片来自GDC 2017, PBR Diffuse Lighting for GGX+SmithMicrosurfaces, Earl Hammon )
https://zhuanlan.zhihu.com/p/33464301?utm_medium=social&utm_source=qq
也不知道怎么滴,PBR突然成了一个你会了就好像什么都会,不会就好像什么都不会的标尺了。。。
PBR不同于其他渲染技术,其实并没有太多可自定义扩展的地方。如果你需要对官方提供的PBR做修改,也就是一些性能调优,需要透彻的理解。
基础概念:微平面和辐射度
这是两个对于PBR非常重要的概念,和光线追踪一同,构成了PBR的物理基础。
然而,其实你并不一定非要去了解它们。因为他们的出现基本上只是为了证明:PBR的“数学公式”,是符合物理的。
几个容易迷惑的点:
1、光源的单位是辐射强度I(每单位角),但在不随距离衰减的直线光中,它与辐射度等价。
2、屏幕的最终颜色值是辐射度L(每单位角单位面积),这也被称为辐射率,或者辐射亮度。辐射度等价于以往的“颜色”。
3、辐射度是最常用的物理量,其他物理量更多情况下是作为公式中的中间值,或者输入参数存在。
4、微平面是微观而非宏观的,所以并不会和任何外部的宏观物理量产生交互,但微平面会导致一些宏观的统计结果(诸如散射)。
1 反射率方程
这是PBR的核心,也是主要的劝退点。哈哈哈哈
lightDir.normal大家都应该很熟悉,如果将镜面反射系数设定为0,漫反射系数设定为1,公式就和单纯的Lambert漫反射基本一致:

不一致的部分是这个除以π。因为它把亮度降低了,就只能相应调高光源的亮度补回来。看似别扭,但是回头一想,光源的亮度,难道不就应该比周围的物品高上很多吗?因为即使是直射,也还是会有很多光线被散射到其他方向,只有少部分才正常投射到了人眼中,漫反射的性质就是如此,之前不除π的做法其实才是错误的。
其实这里的除以π,是为了能量守恒。
另外还有一个地方容易让人迷惑,按说经过半球积分汇集了不同方向的光线后,返回的结果应该是辐照度E(每单位面积),而这个反射率公式左边却是L(每单位角单位面积),这在单位上就说不过去。
实际上,是因为这个公式经过了化简,把一些中间参数给约掉了,剩下的部分形成了这样的结构。这篇文章有推导过程:
https://www.cnblogs.com/jerrycg/p/4932031.html
从“非数学”的角度考虑的话,也可以认为是这个单位面积汇集的不同方向的光线最后都融合并反射了出去,我们从中重新取了一条光线作为结果。
这部分叫做Cook-Torrance 的BRDF光照公式,分子上的三个系数含义如下:
镜面高光:法线分布函数 Normal Distribution Function
参数:normal、viewDir、lightDir、粗糙度
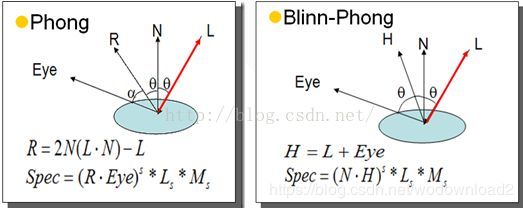
这里和传统的BlinnPhong高光模型一样,是用半角向量h,也就是viewdir和lightdir的中间向量h,和normal求点乘来决定高光亮度的。
了解的朋友都知道,BlinnPhong其实相对于它的前身Phong,并不是那么的“物理”(视线越接近水平和光线反射的物理原理越不一致),所以我看到PBR依然在使用BlinnPhong是有点意外的。
也就说明,两个都不完全“物理”的公式,还是看上去和物理效果更接近的,比实际“更物理”的吃香。经验公式最终获得了胜利(括弧笑)。
而综合了散射系数???这是法线分布函数吧吧。。的具体的公式如下:
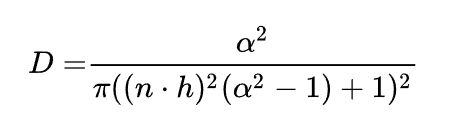
这个公式也是前人的劳动成果,我也不知道是物理推导的结果还是“看上去对就好”的经验公式。但在不同的粗糙度α取值下,它确实和BlinnPhong通过pow实现的效果方向一致,拥有类似的结果。但它的取值是0-1,效果变化也很平滑,比起Skininess那种没谱的参数更容易控制。
当然更重要的是不会辐射出多余的光,D不会大于1/π(除π的原因和上面漫反射部分一致)
当α非常接近0的时候,光照集中在一点,其他方向会完全看不到光线。这是符合现实的。
几何遮蔽:几何函数 Geometry function
参数:normal,viewDir,lightDir,粗糙度
这是一个其他传统光照模型不具有的特征,体现了光在物体粗糙面上反射时的损耗。这不是损耗,而是被遮挡了。。。

效果就是粗糙度越大,亮度越低。但视线和光线越接近垂直,受粗糙度的影响就越小,合情合理。
k的取值范围都在逐渐逼近1/2。而直接光和间接光的差别是,直接光至少有1/8的吸收系数保底,而间接光没有。这是为了让完全光滑的物体,也能至少吸收一些光线。完全不吸收光线的物体是不应该存在的。
菲涅尔方程:Fresnel equation
参数:normal,viewDir,金属度
菲涅尔方程以前一般是用在水体上的,因为水体粗糙度低反光能力强,却又不是金属,是菲涅尔效应最明显的现实物体。
注意:这个公式和光照方向无关。
法线和视线夹角越大(视线越接近水平),F的值也就越大,反射光的亮度也越高,这就是所有物体都具有的菲涅尔效应。即使不是金属物体,在这种情况下都会产生和金属物体类似的表现。而当物体本身就是金属的时候(F0接近1),不管视线是什么情况,F的值都会接近于1,那么菲涅尔效应也就看不出来了。
这看似是个无关紧要的特性——那只是我们大多没有意识到“物体应该如此”而已,但即使我们没注意到,我们的大脑却会依然会得出一个“不真实”的结论。其实菲涅尔效应的模拟比我们想象中要更重要,并不仅仅是在水体模拟这个情景下。
然而,对于金属物体而言,菲涅尔其实并不完全适用。他的F0参数对不同颜色值的反射率是不同的,而且还需要和表面颜色相乘,否则我们的大脑就会通知我们它“不像金属”,所以最终的做法是做这样一次处理:
F0 = mix(vec3(0.04), 表面颜色, 金属度);
这样代入公式的结果就比较符合金属的物理特征,而非金属由于F0值偏低,即使乘了表面颜色影响也不大。
注意这里的表面颜色仅仅是给金属物体用的,用于表现金属物体的特殊性质,高光部分本身并不需要和物体的表面颜色相乘。
BRDF方程的配平系数:
至于这个公式剩下的分母部分,在哪里都没有看到它们的解释,而且也想不出“除点乘”对应着何种物理特性,“4”这个迷之系数更是难以理解。大家都是把它当做一个配平系数直接用了,最后我也只知道这两个点乘是和微平面有关的。
我倒是觉得它们应该不是什么“经验公式”,应该有推导的方法,但这个问题我确实也没找到懂的人,所以这次也只能先放在一边了。
最后还有两个参数没有解明,也就是Kd(漫反射比例)和Ks(镜面反射比例)。
Ks(镜面反射比例)实际上就是F。之前的公式其实并不妥当,因为Ks和F其实是重复的,只需要乘一次。所以应该是:
而Kd(漫反射比例),则是(1-F)(1-金属度),除了需要减掉F外,还要再乘一次(1-金属度)。这是因为金属会更多的吸收折射光线导致漫反射消失,这是金属物质的特殊物理性质。
其实,刚才说的这几个DGF公式都不是唯一的,因为这些公式即使是基于物理的,也还是会包含一些“只要和结果差不多就可以”的部分(比如那个1/8),因为严格的公式往往会为了不明显的细节而消耗大量计算时间,不值得。
所以,他们其实也都只是“并非那么拟合”的拟合公式。
而这几个公式,也有一些精度更低,但性能更好的拟合版本,诸如UE4的Paper里,菲涅尔部分使用的是这样一个神奇的公式:
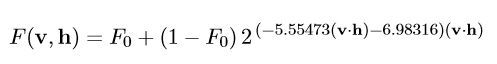
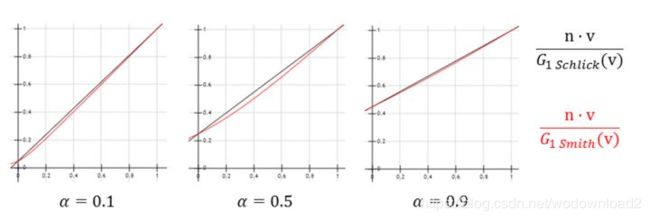
这个公式是用曲线拟合方式对之前那个菲涅尔方程的近似,通过把pow函数换成exp2,得到了更好一点的性能。
2 IBL(Image-Based Lighting 基于纹理的光照)
但是PBR并不是只有直接光照
如果只考虑直接光照的话,PBR渲染出来的画面,其实和以前并没有什么区别。PBR统一了光照的单位,保证了光能守恒,确实有他的积极意义。但是只说画面效果的话,确实没啥明显的进步。
让PBR表现出现优于上一个世纪的画面效果的,是它的环境光照部分。这部分则是由IBL实现的。实际上,他就是所谓的动态全局光照(GI)的正体。
实现原理仅从它的名字(Image-Based)就可以猜出来,就是cubemap(环境贴图)。实际上,它就是我们熟悉的环境反射贴图,只是采样点布点更加广泛,而且会在相近的采样点之间插值。对于Unity而言,就是Light Probe。
只不过,在PBR的IBL中,这张环境贴图并不会仅仅提供非常粗糙的几个光源的烘焙图。它会把周围环境的辐射度(也就是颜色)完整保存起来,而且精度很高,高到可以形成清晰的镜面倒影。
而PBR的材质则会把这种环境贴图当做光源来进行采样。如果是金属材质,且粗糙度低,就能够映射出周围的环境,甚至成为“镜子”。但不是金属的物体也会受此影响,不仅仅会被光源照亮,还会被周围这些“预烘焙成贴图”的物体略微照亮。
实现上确实并不复杂,和环境贴图的用法差不多,直接采样cubemap获得光照数据,然后再代入PBR的公式算出结果就行了。
那么,我们是否应该根据这个积分,采样整个半球的数据,然后再计算一次BRDF,最终合并出一个颜色值呢?
这怎么可能算得动?有脑子的人,肯定都会直接把这个计算结果直接存在环境贴图里好吧?
漫反射部分不需要担心,这部分还真的就是最普通的环境贴图,因为并没有任何变量,直接搞出一张很糊的环境图,再通过normal从cubemap直接采样颜色值即可。

而高光部分,则有粗糙度α这个变数,必须需要烘焙出多个粗糙度下的环境图。然而,不同α值下的烘焙出环境贴图,其实主要就是模糊程度的不同,所以生成这样一组图:

然后合并到一张cubemap的多个mipMap层级上,再利用cubeTexLod函数,根据其粗糙度选择特定层级的两个mipMap层级进行三线插值,就能得到需要的半球积分过的光照颜色值了(当然,是近似的)。
float lod = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
然后通过光照正常计算一次BRDF就好了。这样各个不同粗糙度和金属度的材质就都能从同一张环境贴图里获得需要的数据,并完成各自的渲染。
然而,IBL的难点并不在渲染部分。而是在预烘焙部分。这些模糊的贴图,虽说也不是不能直接用高斯模糊一类的方法完成。但高斯模糊毕竟也只是一种近似,效果还是比不上真正的半球积分的。
我贴的两篇文章,其实大部分的内容都在讲怎么拆积分,通过拆解的积分写出一个4096次sample的随机采样函数,算出一个平均值来,存在纹理上,生成需要的烘焙纹理。
这部分内容实在太多,需要了解的就去看原文吧。不想了解的,也可以直接把它的烘焙部分代码抄走。下面依然是对一些难点的解释:

在烘焙环境贴图的计算里,并没有取当前摄像机viewDir,而是让viewDir直接等于 ![]() 。
。
因为在生成cubemap的时候,viewDir本来也没有意义。所以只能让它一直朝向当前正在绘制的像素。之后使用这个cubemap,根据当前的viewDir重新计算的时候,因为两次的viewDir是不同的,积分合并后的结果当然也是错的。
但也没啥别的方法啊。
就图片里的结果,还算勉强可以接受吧。
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
Hammersley叫做低差异序列,是一种特殊的生成随机数的方法,可以生成一组“并不是那么随机的随机数”。
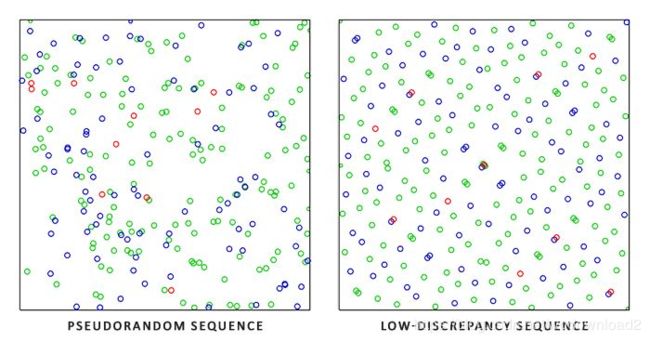
随机数有两大要求:概率分布均匀,足够混乱。Hammersley就是一个概率分布均匀但是并不太混乱的随机数生成方法,作为一个随机数是很糟糕的,但是在随机收敛中使用它代替正常的随机数,反而可以获得更快的收敛速度,也就是在同样sample数量下获得更好的效果。
P.S. 其实这种方法也可以用到抽卡上,能够大幅减少非洲人和欧洲人的比例,在不增加保底的同时提高抽卡体验。
下面的ImportanceSampleGGX(重要性采样)其实很简单,就是“随机正态分布采样”,也就是需要实现一个正态分布的随机数生成器。
正态分布随机的生成方法
z0 = sqrt(-2.0 * log(u1)) * cos(2 * pi * u2);
z1 = sqrt(-2.0 * log(u1)) * sin(2 * pi * u2);
(u1,u2是两个[0-1]的随机数)
和文中的重要性采样代码对比下就能发现他们的公式是多么的相似。
P.S. 其实也可以用到游戏逻辑中,比如角色长期静止时pose动作出现的时机。
除了普通的辐射度烘焙外,它还将IBL的BRDF计算过程做了预计算,放入了一个LUT查找图里。
vec2 envBRDF = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)
用NdotV,roughness作为参数就可以直接从图中获得计算结果,并得到处理了视角和高光的最终颜色值。虽然纹理随机采样会导致cache miss,但毕竟节约了大量的计算。
这张查找图的生成方法,还有那个拆积分的过程……很抱歉我实在没心情去看,实在是又臭又长。
——毕竟这个图其实是通用的啊,复制粘贴走就可以,连代码都不需要抄。