SVM算法的python实现方法
SVM算法的python实现方法
- 前言
- SMO算法的伪代码回顾
- 代码实现
- 完全按照Platt伪代码思路的实现
- 小小的改进
- Coding Tips
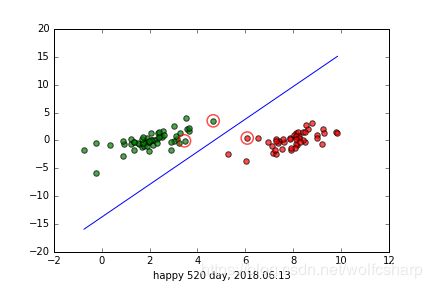
- 运行结果
前言
光说不练花把势,在前面两篇文章SVM的数学原理和SMO(Sequential Minimal Optimization)算法的数学原理花了很多时间把数学问题搞清楚之后,时机已经非常成熟,参照SMO算法的伪代码,编写代码实现并检验一下效果将会是一件振奋又有趣的事情。
SMO算法的伪代码回顾
代码实现
完全按照Platt伪代码思路的实现
'''
#Implement svm algorithm only using basic python
#Author:Leo Ma
#For csmath2019 assignment5,ZheJiang University
#Date:2019.05.20
'''
import numpy as np
import random
import matplotlib.pyplot as plt
'''
类名称:dataStruct
功能:用于存储一些需要保存或者初始化的数据
作者:Leo Ma
时间:2019.05.20
'''
class dataStruct:
def __init__(self,dataMatIn,labelMatIn,C,toler,eps):
self.dataMat = dataMatIn #样本数据
self.labelMat = labelMatIn #样本标签
self.C = C #参数C
self.toler = toler #容错率
self.eps = eps #乘子更新最小比率
self.m = np.shape(dataMatIn)[0] #样本数
self.alphas = np.mat(np.zeros((self.m,1))) #拉格朗日乘子alphas,shape(m,1),初始化全为0
self.b = 0 #参数b,初始化为0
self.eCache = np.mat(np.zeros((self.m,2))) #误差缓存,
'''
函数名称:loadData
函数功能:读取文本文件中的数据,以样本数据和标签的形式返回
输入参数:filename 文本文件名
返回参数:dataMat 样本数据
labelMat 样本标签
作者:Leo Ma
时间:2019.05.20
'''
def loadData(filename):
dataMat = [];labelMat = []
fr = open(filename)
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split('\t') #滤除行首行尾空格,以\t作为分隔符,对这行进行分解
num = np.shape(lineArr)[0]
dataMat.append(list(map(float,lineArr[0:num-1])))#这一行的除最后一个被添加为数据
labelMat.append(float(lineArr[num-1]))#这一行的最后一个数据被添加为标签
dataMat = np.mat(dataMat)
labelMat = np.mat(labelMat).T
return dataMat,labelMat
'''
函数名称:takeStep
函数功能:给定alpha1和alpha2,执行alpha1和alpha2的更新,执行b的更新
输入参数:i1 alpha1的标号
i2 alpha2的标号
dataMat 样本数据
labelMat 样本标签
返回参数:如果i1==i2 or L==H or eta<=0 or alpha更新前后相差太小,返回0
正常执行,返回1
作者:Leo Ma
时间:2019.05.20
'''
def takeStep(i1,i2,dS):
#如果选择了两个相同的乘子,不满足线性等式约束条件,因此不做更新
if(i1 == i2):
print("i1 == i2")
return 0
#从数据结构中取得需要用到的数据
alpha1 = dS.alphas[i1,0]
alpha2 = dS.alphas[i2,0]
y1 = dS.labelMat[i1]
y2 = dS.labelMat[i2]
#如果E1以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E1
if(dS.eCache[i1,0] == 1):
E1 = dS.eCache[i1,1]
else:
u1 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i1,:].T) + dS.b #计算SVM的输出值u1
E1 = float(u1 - y1) #误差E1
#dS.eCache[i1] = [1,E1] #存到cache中
#如果E2以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E2
if(dS.eCache[i2,0] == 1):
E2 = dS.eCache[i2,1]
else:
u2 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i2,:].T) + dS.b #计算SVM的输出值u2
E2 = float(u2 - y2) #误差E2
#dS.eCache[i2] = [1,E2] #存到cache中
s = y1*y2
#计算alpha2的上界H和下界L
if(s==1): #如果y1==y2
L = max(0,alpha1+alpha2-dS.C)
H = min(dS.C,alpha1+alpha2)
elif(s==-1): #如果y1!=y2
L = max(0,alpha2-alpha1)
H = min(dS.C,dS.C+alpha2-alpha1)
if(L==H):
print("L==H")
return 0
#计算学习率eta
k11 = np.dot(dS.dataMat[i1,::],dS.dataMat[i1,:].T)
k12 = np.dot(dS.dataMat[i1,::],dS.dataMat[i2,:].T)
k22 = np.dot(dS.dataMat[i2,::],dS.dataMat[i2,:].T)
eta = k11 - 2*k12 +k22
if(eta > 0):#正常情况下eta是大于0的,此时计算新的alpha2,新的alpha2标记为a2
a2 = alpha2 + y2*(E1-E2)/eta#这个公式的推导,曾经花费了我很多精力,现在写出来却是如此简洁,数学真是个好东西
#对a2进行上下界裁剪
if(a2 < L):
a2 = L
elif(a2 > H):
a2 = H
else:#非正常情况下,也有可能出现eta《=0的情况
print("eta<=0")
return 0
'''
Lobj =
Hobj =
if(Lobj < Hobj-eps):
a2 = L
elif(Lobj > Hobj+eps):
a2 = H
else:
a2 = alpha2
'''
#如果更新量太小,就不值浪费算力继续算a1和b,不值得对这三者进行更新
if(abs(a2-alpha2) < dS.eps*(a2+alpha2+dS.eps)):
print("so small update on alpha2!")
return 0
#计算新的alpha1,标记为a1
a1 = alpha1 + s*(alpha2 - a2)
#计算b1和b2,并且更新b
b1 = -E1 + y1*(alpha1 - a1)*np.dot(dS.dataMat[i1,:],dS.dataMat[i1,:].T) + y2*(alpha2 - a2)*np.dot(dS.dataMat[i1,:],dS.dataMat[i2,:].T) + dS.b
b2 = -E2 + y1*(alpha1 - a1)*np.dot(dS.dataMat[i1,:],dS.dataMat[i2,:].T) + y2*(alpha2 - a2)*np.dot(dS.dataMat[i2,:],dS.dataMat[i2,:].T) + dS.b
if(a1>0 and a10 and a2dS.toler and alpha2>0)):
'''
#随机选择的方法确定另一个乘子alpha1,多执行几次可可以收敛到很好的结果,就是效率比较低
i1 = random.randint(0, dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
'''
#启发式的方法确定另一个乘子alpha1
nonZeroAlphasList = np.nonzero(dS.alphas.A)[0].tolist()#找到所有的非0的alpha
nonCAlphasList = np.nonzero((dS.alphas-dS.C).A)[0].tolist()#找到所有的非C的alpha
nonBoundAlphasList = list(set(nonZeroAlphasList)&set(nonCAlphasList))#所有非边界(既不=0,也不=C)的alpha
#如果非边界的alpha数量至少两个,则在所有的非边界alpha上找到能够使\E1-E2\最大的那个E1,对这一对乘子进行更新
if(len(nonBoundAlphasList) > 1):
maxE = 0
maxEindex = 0
for k in nonBoundAlphasList:
if(abs(dS.eCache[k,1]-E2)>maxE):
maxE = abs(dS.eCache[k,1]-E2)
maxEindex = k
i1 = maxEindex
if(takeStep(i1,i2,dS)):
return 1
#如果上面找到的那个i1没能使alpha和b得到有效更新,则从随机开始处遍历整个非边界alpha作为i1,逐个对每一对乘子尝试进行更新
randomStart = random.randint(0,len(nonBoundAlphasList)-1)
for i1 in range(randomStart,len(nonBoundAlphasList)):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
for i1 in range(0,randomStart):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
#如果上面的更新仍然没有return 1跳出去或者非边界alpha数量少于两个,这种情况只好从随机开始的位置开始遍历整个可能的i1,对每一对尝试更新
randomStart = random.randint(0,dS.m-1)
for i1 in range(randomStart,dS.m):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
for i1 in range(0,randomStart):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
'''
i1 = random.randint(0,dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
'''
#如果实在还更新不了,就回去重新选择一个alpha2吧,当前的alpha2肯定是有毒
return 0
'''
函数名称:SVM_with_SMO
函数功能:用SMO写的SVM的入口函数,里面采用了第一个启发式确定alpha2,即在全局遍历和非边界遍历之间来回repeat,直到不再有任何更新
输入参数:dS dataStruct类的数据
返回参数:None
作者:Leo Ma
时间:2019.05.20
'''
def SVM_with_SMO(dS):
#初始化控制变量,确保第一次要全局遍历
numChanged = 0
examineAll = 1
#显然,如果全局遍历了一次,并且没有任何更新,此时examineAll和numChanged都会被置零,算法终止
while(numChanged > 0 or examineAll):
numChanged = 0
if(examineAll):
for i in range(dS.m):
numChanged += examineExample(i,dS)
else:
for i in range(dS.m):
if(dS.alphas[i] == 0 or dS.alphas[i] == dS.C):continue
numChanged += examineExample(i,dS)
if(examineAll == 1):
examineAll = 0
elif(numChanged == 0):
examineAll = 1
'''
函数名称:cal_W
函数功能:根据alpha和y来计算W
输入参数:dS dataStruct类的数据
返回参数:W 超平名的法向量W
作者:Leo Ma
时间:2019.05.20
'''
def cal_W(dS):
W = np.dot(dS.dataMat.T,np.multiply(dS.labelMat,dS.alphas))
return W
'''
函数名称:showClassifer
函数功能:画出原始数据点、超平面,并标出支持向量
输入参数:dS dataStruct类的数据
W 超平名的法向量W
返回参数:None
作者:机器学习实践SVM chapter 6
修改:Leo Ma
时间:2019.05.20
'''
def showClassifer(dS,w):
#绘制样本点
dataMat = dS.dataMat.tolist()
data_plus = [] #正样本
data_minus = [] #负样本
for i in range(len(dataMat)):
if dS.labelMat[i,0] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7, c='r') #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7,c='g') #负样本散点图
#绘制直线
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(dS.b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
#找出支持向量点
for i, alpha in enumerate(dS.alphas):
if abs(alpha) > 0.000000001:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.xlabel("happy 520 day, 2018.06.13")
plt.savefig("svm.png")
plt.show()
if __name__ == '__main__':
dataMat,labelMat = loadData("testSet.txt")
dS = dataStruct(dataMat, labelMat, 0.6, 0.001, 0.01)#初始化数据结构 dataMatIn, labelMatIn,C,toler,eps
for i in range(0,1):#只需要执行一次,效果就非常不错
SVM_with_SMO(dS)
W = cal_W(dS)
showClassifer(dS,W.tolist())
小小的改进
在实际运行中,发现原文中第二个启发式,即确定拉格朗日乘子alpha1的过程中,存在一些cpu算力浪费的现象:
1.在函数examineExample()中,对于使|E1-E2|最大的alpha1不能有效更新的情况,原启发式将会从随机起点处遍历所有的非边界alpha,逐一对其进行可能的更新,由于非边界alpha数量很少(大部分alpha=0),并且非边界alpha上更新更有效,原启发式对这一部分的处理合情合理完满
2.但是,在遍历所有非边界alpha后,仍然不能有效更新的情况,或者非边界alpha数量小于2,原启发式将会从随机起点处遍历所有可能的alpha,逐一对其进行可能的更新。这种策略实际运行中效率十分低下,主要原因是遍历所有的alpha使之与alpha2形成一对拉格朗日乘子,每次计算的alpha2的更新值a2,都会非常靠近alpha2,更新量太小根本不值得更新,但是这个过程却要花费算力去计算a2,因此效率很低
3.一个合理的想法是,将从随机起点处遍历所有可能的alpha变换为:
在所有可能的alpha中随机选择一个作为alpha1,对乘子对(alpha1,alpha2)尝试更新only once,若更新不成功,就直接跳出examineExample(),以期待一个更优秀的alpha2
这样就可以将大量的算力用在真正大步长更新的乘子对上,会显著加快收敛速度
改进的examineExample():
'''
函数名称:examineExample
函数功能:给定alpha2,如果alpha2不满足KKT条件,则再找一个alpha1,对这两个乘子进行一次takeStep
输入参数:i2 alpha的标号
dataMat 样本数据
labelMat 样本标签
返回参数:如果成功对一对乘子alpha1和alpha2执行了一次takeStep,返回1;否则,返回0
作者:Leo Ma
时间:2019.05.20
'''
def examineExample(i2,dS):
#从数据结构中取得需要用到的数据
y2 = dS.labelMat[i2,0]
alpha2 = dS.alphas[i2,0]
#如果E2以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E2
if(dS.eCache[i2,0] == 1):
E2 = dS.eCache[i2,1]
else:
u2 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i2,:].T) + dS.b#计算SVM的输出值u2
E2 = float(u2 - y2)#误差E2
#dS.eCache[i2] = [1,E2]
r2 = E2*y2
#如果当前的alpha2在一定容忍误差内不满足KKT条件,则需要对其进行更新
if((r2<-dS.toler and alpha2dS.toler and alpha2>0)):
'''
#随机选择的方法确定另一个乘子alpha1,多执行几次可可以收敛到很好的结果,就是效率比较低
i1 = random.randint(0, dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
'''
#启发式的方法确定另一个乘子alpha1
nonZeroAlphasList = np.nonzero(dS.alphas.A)[0].tolist()#找到所有的非0的alpha
nonCAlphasList = np.nonzero((dS.alphas-dS.C).A)[0].tolist()#找到所有的非C的alpha
nonBoundAlphasList = list(set(nonZeroAlphasList)&set(nonCAlphasList))#所有非边界(既不=0,也不=C)的alpha
#如果非边界的alpha数量至少两个,则在所有的非边界alpha上找到能够使\E1-E2\最大的那个E1,对这一对乘子进行更新
if(len(nonBoundAlphasList) > 1):
maxE = 0
maxEindex = 0
for k in nonBoundAlphasList:
if(abs(dS.eCache[k,1]-E2)>maxE):
maxE = abs(dS.eCache[k,1]-E2)
maxEindex = k
i1 = maxEindex
if(takeStep(i1,i2,dS)):
return 1
#如果上面找到的那个i1没能使alpha和b得到有效更新,则从随机开始处遍历整个非边界alpha作为i1,逐个对每一对乘子尝试进行更新
randomStart = random.randint(0,len(nonBoundAlphasList)-1)
for i1 in range(randomStart,len(nonBoundAlphasList)):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
for i1 in range(0,randomStart):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
#如果上面的更新仍然没有return 1跳出去或者非边界alpha数量少于两个,在所有可能的alpha上随机挑一个alpha1,尝试更新一次,如果还不行就跳出本函数,及时止损
i1 = random.randint(0,dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
#如果实在还更新不了,就回去重新选择一个alpha2吧,当前的alpha2肯定是有毒
return 0
Coding Tips
1.用非启发式的方法,多迭代几次也能跑出不错的结果
2.在用第二个启发式策略的时候,误差Ecache只要更新那些alpha非零的项。如果全部更新Ecache,则会造成算法陷入局部极值点,即用使最大化|E1-E2|的方式每次选出的alpha1都是基本相同的,此时陷入饱和。这将会是一件会让人心情很糟糕的事情。
3.只有每次在takeStep()中完成了alpha1、alpha2、b的更新之后,才需要重新计算Ecache
4.在非Ecache更新的所有其他地方,如果要用到E1和E2,应该先查询Ecache中是否已经计算得到,如果Ecache中已经保存有记录,则直接赋值。否则,新计算E1或者E2,这些新计算的结果一定不要存到Ecache中,这样可以保证Ecache的相对于alpha是干净的。