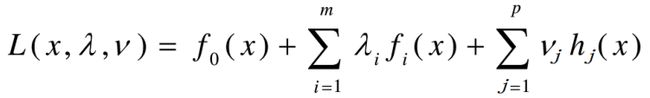凸优化 - 4 - 凸优化、Lagrange乘子法、KKT条件
本总结是是个人为防止遗忘而作,不得转载和商用。
前提说明:为了方便查阅,我将整个凸优化的内容分成了很多部分,因为后面的部分用到了前面的知识,所以,如果你的目的是查看后面的内容但对前面的某个知识点不甚了解的话可以根据标题查看前面的部分。
凸优化
终于到凸优化了....
什么是凸优化问题呢?是这样。
慢慢的我们会遇到这样的优化问题:
求f(x),x∈Rn的极小值
其中f(x)有一些约束,这里假设有:
一个等式约束hj(x)= 0
一个不等式约束fi(x)≤0
这样的问题很常见吧(不常见的话慢慢你会常见的--....)。
此时,如果f(x)和fi(x)都是凸函数,hj(x)是仿射/线性函数的话,这样的问题就是凸优化问题,就酱(摊手)。
PS:一般提到凸优化我们都是求其最小值(为啥?都说了凸优化问题中f(x)和fi(x)都是凸函数,凸函数你给我求个最大值试试?),这就是为啥你看一些教材中一碰到求极值,即使f(x)是凹函数需要求极大值时也会来一句“习惯上我们求最小值”,然后“啪”一下给f(x)加个负号转化成求极小的原因,这个习惯就是解凸优化解习惯了! (╯‵□′)╯︵┻━┻
Lagrange乘子法
一般我们遇到优化问题时是不会管这个是不是凸优化问题的,而求解优化问题一般使用Lagrange乘子法,对于一般优化问题:
其Lagrange函数如下:
其中λ≥ 0,v ∈ R。
话说这个在大一就学了,忘了的翻高数,关于公式我就不解释了,这里说说其他的。
对于Lagrange函数,如果把等号右边的第二项拆开后可以写成下面的样子:
![]()
这时如果把L(x,λ,v)看成关于λ1的函数的话,f1(x)就是λ1的系数,λ1f1(x)右边那些就是λ1的常数,于是L(x,λ,v)关于λ1就是一条直线!或者说L(x,λ,v)关于λ1的仿射函数。
同理,L(x,λ,v)关于所有的λ和v都是仿射函数!于是你就可以在脑海中想象一下m+p条直线相交的画面了。在此情况下,L(x,λ,v)的上确界就是个凸函数!L(x,λ,v)的下确界就是凹函数!因此,如果对L(x,λ,v)求其关于x的下确界的极大值(PS:它离上确界的最小值很近会相等)的话,其结果就是个关于λ,v的函数(求关于x的下确界后x就没了),这里将这个函数写成g(λ,v),而这个函数就是Lagrange对偶函数!而上面已经说明:Lagrange对偶函数是凹函数。
为了方面下面说明,之后就用L(x,λ)代表Lagrange函数,g(λ)代表该Lagrange函数的对偶函数。
之前说了这么一大堆,那到底为什么需要弄个Lagrange函数,然后为什么还需要弄个对偶函数?我对原函数直接求极小值不得了?
而这个的答案是:被那几个约束条件一搞后....咱们压根不知道f(x)的样子好吧!你求啊!你求啊!!你对f(x)直接求偏导得出个结果压根不满足约束条件还搞毛啊,所以我们需要Lagrange函数,而为什么需要Lagrange的对偶函数是因为:有时候真心不方便求f(x)的极小值,但求出Lagrange的对偶函数后发现,求对偶函数挺方便的,于是让对偶函数的最大值代替原函数的最小值,这起码是个估计嘛。
好了,能解释的就这样了,下面总结一下:
我们的目标是求原函数f(x)的最小值,但是原函数有些约束条件,于是需要将其写成Lagrange函数,即L(x,λ) = f(x) +λg(x)。
正常情况是先对λ求极大(得到L(x,λ)的上确界),然后对x求极小,从而得到原函数的极小值,即:min_x max_λ L(x,λ)。
但是有时候上面的做法十分不好求,于是只好先对L(x,λ)的x求极小(获得L(x,λ)的下确界)从而得到L(x,λ)的对偶函数g(λ),然后后对g(λ)求极大来近似原函数f(x)的最小值,即:max_λmin_x L(x,λ)
KKT条件
在“Lagrange乘子法”有这么一句话“让对偶函数的最大值代替原函数的最小值,这起码是个估计嘛”,为什么说是个估计?原因见下面的式子。
上式的g(λ*,v*)就是Lagrange对偶函数,而根据定义g(λ*,v*)对Lagrange函数求下界,即第二行(括号里是Lagrange函数,外面的inf就是求下界的意思)。那既然是求下界,则g(λ*,v*)的值一定小于等于Lagrange函数吧,于是第三行就出来了,这时候别忘了,根据Lagrange函数的定义,λi是大于等于0的,fi(x*)≤0,hi(x*)=0,于是第三行的第二项是小于等于0的,第三行的第三项等于0,因此f0(x*)加上一个小于等于0的数再加上一个等于0的数,其结果一定小于等于f0(x*)的。
这就是为什么之前说“让对偶函数的最大值代替原函数的最小值,这起码是个估计嘛”,这是因为对偶函数求得的极大值是小于等于原函数的极小值的,即:对偶函数的结果≤我们的目标值。
既然如此,如何让≤变成=就是我们的目标了,即:将上面图中的第三行和第四行的两个不等号都换成等号!因此我们需要这样做:
1, 为了让第三行的≤变成=,我们需要让第三行的x*是第二行Lagrange函数的一个驻点,即:让Lagrange函数对x求偏导的值=0,即:▽xL(x,λ) = 0。
2, 为了让第四行的≤变成=,我们需要让每个λi*fi(x*)= 0,因为λi≥0,fi(x*)是已知的约束条件,是小于等于0的,所有若有一个λi*fi(x*)≠0,则第三行第二项的值就一定小于0,这样就无法将≤变成=,然后因为hi(x*)是已知的约束条件,是等于0的。
这样一来,就可以让所有的≤变成=,于是就达成我们的目标了。
现在让我们总结下为了让所有的≤变成=,需要满足什么条件:
1, ▽xL(x,λ) = 0 (为了达到目标,而增加的新约束)
2, λi*fi(x*) = 0 (为了达到目标,而增加的新约束)
3, λi≥0 (Lagrange乘子法的定义)
4, fi(x*)≤0 (已知的约束条件)
5, hi(x*) = 0 (已知的约束条件)
而这5个条件合起来就叫KKT条件!
注意:如果原问题中fi(x)是凸函数的话,KKT条件是充分条件;如果原问题是个一般性问题,即fi(x)不一定是凸函数,则KKT条件是必要条件,不是充分条件。