李宏毅机器学习——无监督学习(一)
引言
本文主要探讨无监督学习的线性方法(Linear Methods)。
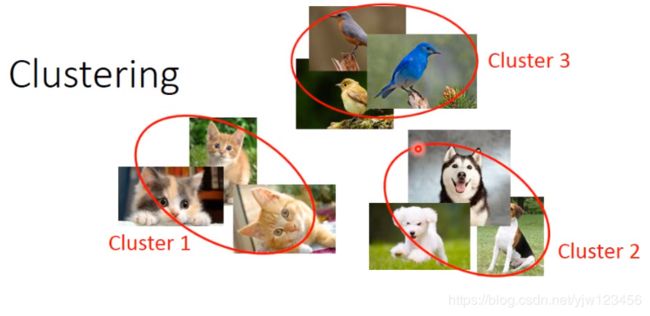
聚类
把很多不同的图像,根据它们的相似度分成不同的组(类别),问题是要分成多少个组。
最常用的方法有:
K-means
- 聚类 N N N个数据 X = { x 1 , ⋯ , x n , x N } X=\{x^1,\cdots,x^n,x^N\} X={x1,⋯,xn,xN} 到 K K K个组
- 初始化 K K K个分组中心点: c i , i = 1 , 2 , ⋯ , K c^i,i=1,2,\cdots,K ci,i=1,2,⋯,K,可以从 X X X中随机 K K K个点出来
- 重复
- 对 X X X中的所有数据 x n x^n xn:如果 x n x^n xn最接近 c i c^i ci ,那么 x n x^n xn就属于 c i c^i ci,同时令 b i n = 1 b^n_i=1 bin=1;否则令 b i n = 0 b^n_i=0 bin=0
- 更新所有的中心点 c i = ∑ x n b i n x n / ∑ x n b i n c^i = \sum_{x^n}b^n_ix^n/\sum_{x^n}b^n_i ci=∑xnbinxn/∑xnbin
层次凝聚聚类算法(Hierarchical Agglomerative Clustering,HAC)
- 步骤一:建一个树

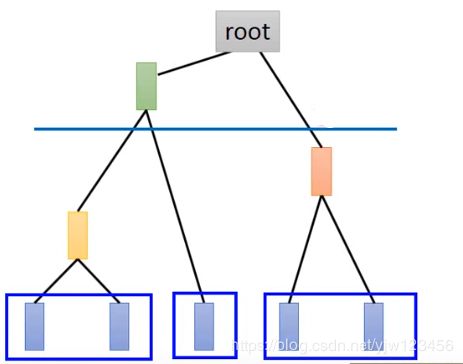
假设有5个样本,这种方法怎么聚类呢,首先把这5个样本相互之间计算相似度,然后选择最相似的两个合并成一个新的样本6。现在只剩下4个样本了,再计算之间的相似度,把最相似的两个数据合并起来,这里假设是4,5合并成了7。同理,最后只剩2个样本8和7。它们之间有共同的父节点root。
- 步骤二:选取一条分割线(threshold)
降维(Dimension Reduction)
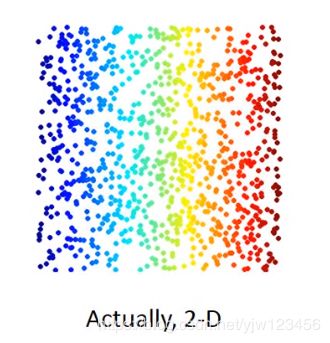
假设你的数据从三维空间看是长这样的,但是用三维来描述它是不必要的。可以通过二维的图像来描述它。
比如在MNIST的手写数字识别中,一个图像有28*28的。实际上其中大多数像素点代表的东西并不是数字,可能是空白啥的。
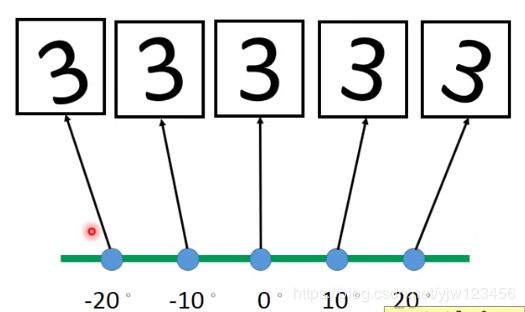
一个极端的例子是把数字三按不同的角度进行旋转。
只要知道其中一幅图像和它的角度,就可以知道其他图像。
那怎么做降维呢。
还是要找到一个函数,它的输入是向量 x x x,输出是向量 z z z,其中 z z z的维度必须必 x x x小。
其中最简单的方法是特征选择(Feature selection)
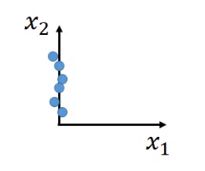
最简单的情况是, x 1 x_1 x1这个维度的特征完全没用,我们就可以直接只选择 x 2 x_2 x2这个维度。但是这种情况比较罕见。通常每个维度或多或少都有一定的作用。
有一种常见的方法叫主成分分析(Principle component analysis,PCA)
这个 z = W x z=Wx z=Wx是个很简单的线性函数,输入 x x x和输出 z z z之间的关系,就是一个线性的转换。
现在要做的事情就是根据很多输入,找出这个 W W W。
假设我们要降到1维的情况。此时 z z z就是一个标量, W W W是行向量:
z 1 = w 1 ⋅ x z_1=w^1 \cdot x z1=w1⋅x , w 1 w^1 w1表示 W W W的第一行,我们把 x x x与 w 1 w^1 w1做内积,得到 z 1 z_1 z1
假设 w 1 w^1 w1的长度是1, ∣ ∣ w 1 ∣ ∣ 2 = 1 ||w^1||_2=1 ∣∣w1∣∣2=1
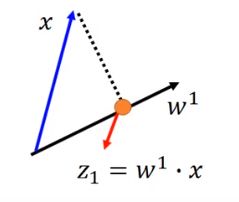
意味着 z 1 z_1 z1是 x x x在 w 1 w^1 w1上的投影。
现在问题是应该选哪个 w 1 w^1 w1
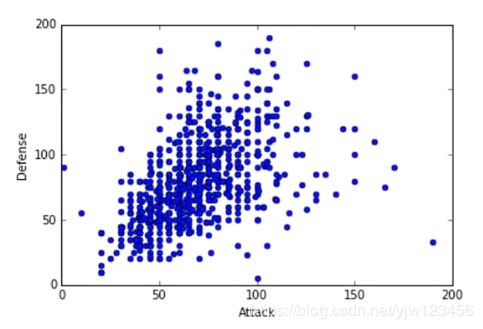
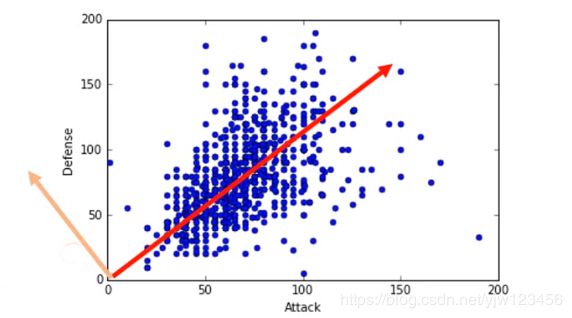
假设上图中的每个点代表一只宝可梦,横坐标是攻击力,纵坐标是防御力。把二维投影到一维,应该要选什么样的 w 1 w^1 w1呢
上图的两个带箭头的直线代表两个不同的 w 1 w^1 w1,我们希望经过投影后得到的 z 1 z_1 z1分布越大越好。即经过投影后还能保持数据点之间的区别。
在上面的例子中,可以看出如果选择红线,点的分布会大一点。
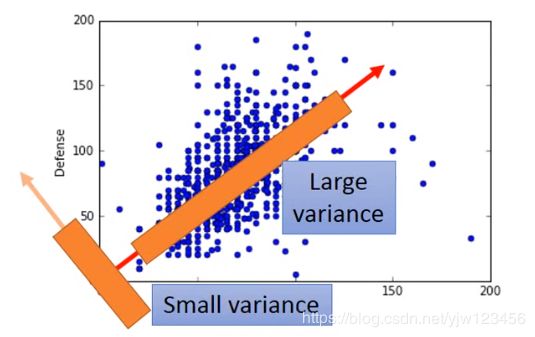
选择的 w 1 w^1 w1可能是具有具体意义的,比如这里这个 w 1 w^1 w1代表宝可梦的强度。
如果用式子来表示的话,就是需要最大化 z 1 z_1 z1的方差:
V a r ( z 1 ) = ∑ z 1 ( z 1 − z 1 ‾ ) 2 Var(z_1) = \sum_{z_1} (z_1 - \overline{z_1})^2 Var(z1)=z1∑(z1−z1)2
如果想投影到二维的平面上,这是把 x x x和另外的 w 2 w^2 w2做内积可以得到 z 2 z_2 z2。
首先 w 2 w^2 w2的长度也是1。
V a r ( z 2 ) = ∑ z 2 ( z 2 − z 2 ‾ ) 2 Var(z_2) = \sum_{z_2} (z_2 - \overline{z_2})^2 Var(z2)=z2∑(z2−z2)2
同时也要最大化 z 2 z_2 z2。但是如果仅仅是这样那不就和找 w 1 w^1 w1的做法是一样的,因此这里需要增加一点东西,我们限制 w 1 ⋅ w 2 = 0 w^1\cdot w^2 = 0 w1⋅w2=0,即它们之间的内积是0。
参考
- 李宏毅机器学习