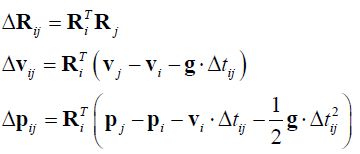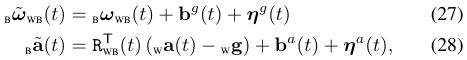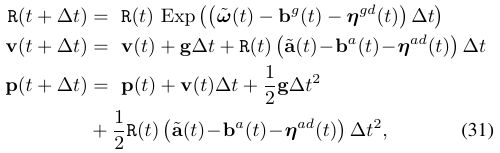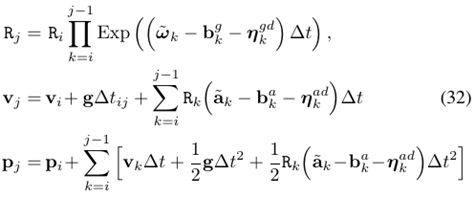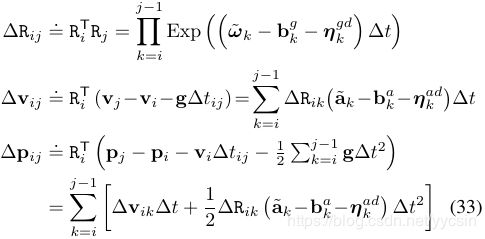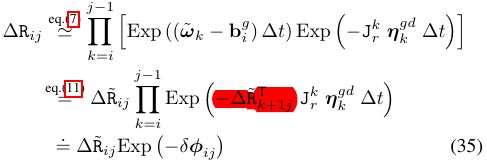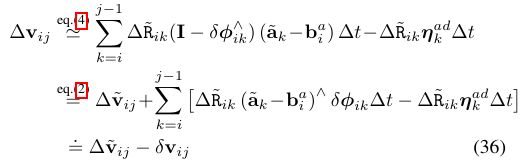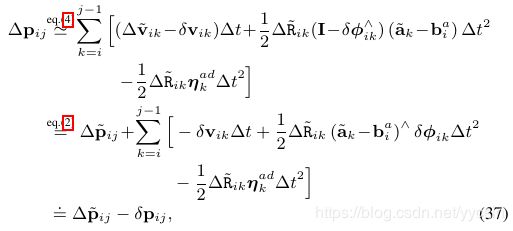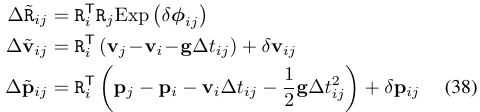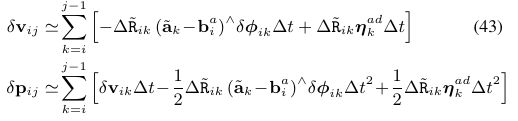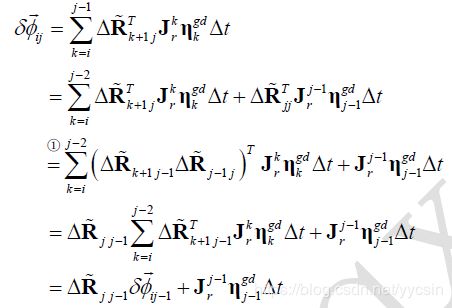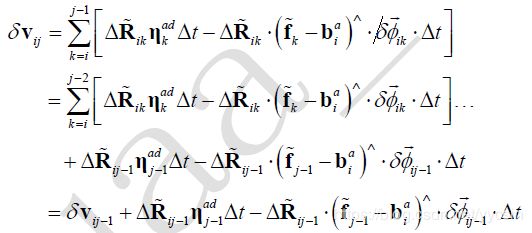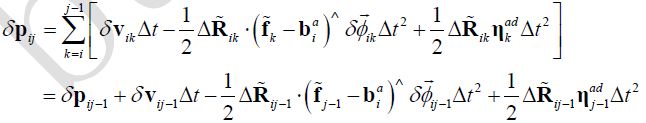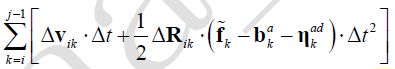IMU预积分的一些理解

IMU预积分，算是比较简单的一个算法，无奈网上找到的资料都讲的晦涩难懂，看明白了也觉得不过如此。

讲一下我的理解：

整体流程

1. 推导IMU离散运动方程

2. 根据离散运动方程，进行预积分，并将预积分的误差项拆分出来，因为我们在定义误差的时候，有P，V，和R，所以不同的误差其实权重是不一样的，我们需要误差项的协方差矩阵来定义这个权重；

3. 因为（测量值=真实值+误差 当然对于R是乘的关系），所以我们可以写出来这个式子：

4. 误差项拆分出来之后，因为我们的加表和陀螺仪的偏置，之前假定是恒定的，但实际上是一个随机游走过程，因此，我们需要考虑偏置的更新；考虑到偏置的原因，我们可以将测量值重新定义如下：

 

          这个公式中，头顶一横杠的是用原有的偏置计算出来的值，头顶是波浪线的是更新的偏置算出来的值；

5. 到这里，我们已经把测量值的表达式搞清楚了，无非是真实值，加上误差值，加上偏置的随机游走导致的波动值，这三项，现在这三项都加进去了，我们可以定义从i到j的预积分的误差值了。实际中我们优化的是误差值，使误差值为0

         理想值：

           根据第四步得到的测量值描述公式，我们得到误差描述公式：

 

6. 到这里还没结束，我们要优化的值，那么我们有误差了，我们需要误差对这些值的导数，即求雅克比，比较繁琐，可以参考资料。求得了导数，误差，我们就可以用G2O进行计算了，真是美极了；

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

下面对其过程进行简要的描述：

IMU数据包含两部分，一部分是加表的数据，另一部分是陀螺仪的数据。我们通过这俩玩意儿可以观测到加速度和角速度，不过我们观察到的数据与实际值还有噪声和偏置，特别是低成本的IMU，这些导致的误差会更厉害

这俩公式就是模型部分了，偏差为b，噪声为η

我们还要知道，当增加一个小的时间时，R，V，P是如何变化的，即以下公式：

考虑到迭代，需要有初始i时刻，结束j时刻，以上公式改写：

 

这个时候，我们要清楚我们最终目的是干嘛，我们是想让他与i时刻的数据解耦，所以我要做一个从i到j 的变化量（对于R要考虑李代数的形式）

上面的这个公式是一个混沌体，既包括测量值，又包括偏置，又包括噪声，这么多玩意儿，如何处理？偏置不知道，我们就假定偏置是恒定的，我们先把噪声分离出来：

 

 

 

具体推导过程网上资料非常丰富，直接写上面的结果了。

到这里已经把误差项分离出来了，上式的左边是测量值，右边第一项是真实值，第二项是噪声值；我们可以把误差项单独拎出来，如下公式：

通过演化，推导，得到误差的一步递推公式：

从这几个公式可以看出来，从i时刻到J时刻，其实是一个时间段，那这个一步递推其实是针对这个时间段的叠加，因此在处理的时候，协方差也需要每个时刻都更新，从i时刻不断更新，直至j时刻。这个协方差可以在求解时，设置信息矩阵的时候用，度量误差中各个维度的权重；

剩下的就是针对测量值的推导描述了，测量值肯定不是只有噪声一项的，测量值除了噪声其实还有偏置导致的偏移，等等，在上面流程介绍中已经讲过了，具体如何推导，网上大把资料。

--------------------------------------------------------------------------------------------------------------------------------------------------------------------

那了解了这些理论知识了，我们需要知道在实际中如何使用呢？

实际中来了IMU的数据之后，我们要如何处理：

1. 根据每一个时刻的IMU值，求delta_P，delta_V，delta_R这三个值就是纯运动方程就可以求了，递推性质，可以最终得到从I到j时刻的delta的总和；
2. 递推求从i到J时刻delta的P，R，V对两个偏置的雅克比的值，这些值后面会用到
3. 这一个时间段的delta的PVR都计算完了，雅克比也计算完了，那就对误差进行更新吧
4. 使用G2O进行对误差的优化，那就使用G2O进行愉快的计算吧

定义误差，

举个例子，针对deltaP中，这个就是从i到j时间段的累计，如何算呢，直接用下面的式子就可以计算了

因为是测量值，实际上已经考虑到噪声了，偏置用上一次的值就好（反正是迭代的）。

定义雅克比：

根据大佬的论文On-Manifold Preintegration for Real-Time Visual-Inertial Odometry，看着公式直接往上整就对了（想自己推导也可以，比较繁琐，但不复杂），无非就是误差方程对P，对R，对V和对偏置求导，其中第2步的求带结果在这个地方是有用的，根源在于这个误差对偏置的求导，和第2步对偏置求导结果部分是相似的，无非就是一个负号的区别，所以可以拿来用。不过deltaR对bg的求导结果还是差异很大的，注意一下。

更新更新，误差最小即可。