How Powerful are Graph Neural Networks? GIN 图同构网络 ICLR 2019 论文详解
文章目录
- 1 相关介绍
- Definition 1 :multiset
- 数学上的单射(injective)
- 2 GNN 怎么和 Weisfeiler-Lehman test 关联起来?
- 2.1 符号定义
- 2.2 Graph Neural Networks
- 2.3 两类任务
- 2.3 Weisfeiler-Lehman test 图同构测试
- 3 WL test 是GNN性能的上限
- Lemma 2
- 4 什么样的GNN 可以和WL test 一样强大?
- Theorem 3
- 5 构建一个强大的图神经网络GIN
- 5.1 Graph Isomorphism Network (GIN) 图同构网络
- 5.2 Graph-level Readout of GIN
- 6 为何基于mean、max aggregate的GNN不够强大?
- 6.1 mean和max 无法区分哪些结构
- 6.2 sum, mean, max 分别可以捕获什么信息?
- 7 实验
- Datasets
- Baselines
- 拟合能力——train效果
- 关注泛化能力——test集效果
- 8 讨论
论文:How Powerful are Graph Neural Networks?
作者:来自于斯坦福的Keyulu Xu,Weihua Hu,Jure Leskovec等人
来源:ICLR 2019的Oral文章
论文链接:https://arxiv.org/pdf/1810.00826.pdf
github链接:https://github.com/weihua916/powerful-gnns
GNN目前主流的做法是递归迭代聚合一阶邻域表征来更新节点表示,如GCN和 GraphSAGE,但这些方法大多是经验主义,缺乏理论去理解GNN到底做了什么,还有什么改进空间。本文基于Weisfeiler-Lehman(WL) test 视角理论分析了GNN,本文的贡献:
- 证明了GNN最多只和 Weisfeiler-Lehman (WL) test 一样有效,即WL test 是GNN性能的上限
- 提供了如何构建GNN,使得和WL一样有效
- 用该框架分析了GCN和GraphSAGE等主流GNNs在捕获图结构上的不足和特性
- 建立了一个简单的神经结构——图同构网络(GIN),并证明了它的判别/表达能力和WL测试一样
1 相关介绍
文中提出了一个理论框架去分析GNNs的表达能力。在学习表示和区分不同的图结构时,描述了不同GNN变体的表达能力。Weisfeiler-Lehman 图同构测试(1968)(WL)是一种强大的检验方法,可以区分大量的图。与GNNs类似,WL测试通过聚集网络邻居的特征向量迭代地更新给定节点的特征向量。WL测试之所以如此强大,是因为它的单射聚合更新将不同的节点邻居映射到不同的特征向量。作者的主要观点是,如果GNN的聚合方案具有高度表达性,并且能够对单射函数建模,那么GNN可以具有与WL测试同样大的区分能力。
为了在数学上形式化上述观点,文中提出的框架首先将给定节点的邻居的特征向量集表示为一个multiset,即,一个可能有重复元素的集合。然后,可以将GNNs中的邻居聚合看作是multiset上的聚合函数。因此,为了拥有强大的表示能力,GNN必须能够将不同的multiset聚合到不同的表示中。文中严格地研究了multiset函数的几个变体,并从理论上描述了它们的区分能力,即,不同的聚合函数如何区分不同的multiset。multiset函数的判别能力越强,GNN的表示能力就越强。
GNNs的表达能力是捕获图结构的关键。文中通过在图分类数据集上的实验来验证理论,对比了使用各种聚合函数的GNNs的性能。
实验结果表明,在作者的理论中最强大的GNN,即图同构网络(GIN),根据经验判断也具有很高的表示能力,因为它几乎完全适合训练数据,而较弱的GNN变体往往严重不适合训练数据。此外,这种表达能力更强的GNN在测试集精度方面优于其他GNNs,并且在许多图分类benchmarks上实现了最先进的性能。
Definition 1 :multiset
multiset是一个广义的集合概念,它允许有重复的元素。更正式地说,一个multiset是一个2元组 X = ( S , m ) X=(S, m) X=(S,m),其中 S S S是由 X X X的不同的元素组成的子集, m : S → N ≥ 1 m: S \rightarrow \mathbb{N}_{\geq 1} m:S→N≥1表示了元素的多样性。文中的multiset就是节点邻居的特征向量集。
数学上的单射(injective)
在数学里,单射函数为一函数,其将不同的引数连接至不同的值上。更精确地说,函数f被称为是单射时,对每一值域内的y,存在至多一个定义域内的x使得f(x) = y。
另一种说法为,f为单射,当f(a) = f(b),则a = b(若a≠b,则f(a)≠f(b)),其中a、b属于定义域。
单射在某些书中也叫入射,可理解成“原不同则像不同”。
2 GNN 怎么和 Weisfeiler-Lehman test 关联起来?
2.1 符号定义
- 图: G = ( V , E ) G=(V, E) G=(V,E)
- V V V是图的节点集
- D = diag ( d 1 , … , d n ) \mathbf{D}=\operatorname{diag}\left(d_{1}, \ldots, d_{n}\right) D=diag(d1,…,dn)代表度矩阵, d i = ∑ j a i j d_{i}=\sum_{j} a_{i j} di=∑jaij
- y i ∈ { 0 , 1 } C \mathbf{y}_{i} \in\{0,1\}^{C} yi∈{0,1}C表示 C C C维的节点one-hot标签
- { G 1 , … , G N } ⊆ G \left\{G_{1}, \dots, G_{N}\right\} \subseteq \mathcal{G} {G1,…,GN}⊆G一个图的集合
- X v X_v Xv表示节点 v v v的特征向量
- h v h_v hv表示需要去学习的节点 v v v的表示向量
- y v = f ( h v ) y_v=f(h_v) yv=f(hv)节点 v v v预测的标签
- h G h_G hG图 G G G的表示向量
- y G = h ( h G ) y_G=h(h_G) yG=h(hG)表示整个图 G G G预测的标签
2.2 Graph Neural Networks
GNNs的目标是以图结构数据和节点特征作为输入,以学习到节点(或图)的表示,用于分类任务。
基于邻域聚合的GNN可以拆分为以下三个模块:
- Aggregate:聚合一阶邻域特征。
- Combine:将邻居聚合的特征与当前节点特征合并,以更新当前节点特征。
- Readout(可选,针对图分类):如果是对graph分类,需要将graph中所有节点特征转变成graph特征。
目前的GNNs都遵循一个邻居聚合的策略,也就是通过聚合邻居的表示然后迭代地更新自己的表示。在 k k k次迭代聚合后就可以捕获到在k-hop邻居内的结构信息。一个 k k k层的GNNs可以表示为:
a v ( k ) = AGGREGATE ( k ) ( { h u ( k − 1 ) : u ∈ N ( v ) } ) , h v ( k ) = COMBINE ( k ) ( h v ( k − 1 ) , a v ( k ) ) (1) \tag{1} a_{v}^{(k)}=\operatorname{AGGREGATE}^{(k)}\left(\left\{h_{u}^{(k-1)}: u \in \mathcal{N}(v)\right\}\right), \quad h_{v}^{(k)}=\operatorname{COMBINE}^{(k)}\left(h_{v}^{(k-1)}, a_{v}^{(k)}\right) av(k)=AGGREGATE(k)({hu(k−1):u∈N(v)}),hv(k)=COMBINE(k)(hv(k−1),av(k))(1)
因此,可以看出AGGREGATE聚合函数和COMBINE连接函数是非常重要的。
GraphSAGE里的pooling AGGREGATE函数为:
a v ( k ) = MAX ( { ReLU ( W ⋅ h u ( k − 1 ) ) , ∀ u ∈ N ( v ) } ) (2) \tag{2} a_{v}^{(k)}=\operatorname{MAX}\left(\left\{\operatorname{ReLU}\left(W \cdot h_{u}^{(k-1)}\right), \forall u \in \mathcal{N}(v)\right\}\right) av(k)=MAX({ReLU(W⋅hu(k−1)),∀u∈N(v)})(2)
其中 W W W是一个可学习的矩阵。COMBINE步骤可以是一个连接,然后是一个线性映射 W ⋅ [ h v ( k − 1 ) , a v ( k ) ] W \cdot\left[h_{v}^{(k-1)}, a_{v}^{(k)}\right] W⋅[hv(k−1),av(k)]。
GCN论文中的AGGREGATEHE(是一个mean pooling)和COMBINE步骤为:
h v ( k ) = ReLU ( W ⋅ MEAN { h u ( k − 1 ) , ∀ u ∈ N ( v ) ∪ { v } } ) (3) \tag{3} h_{v}^{(k)}=\operatorname{ReLU}\left(W \cdot \operatorname{MEAN}\left\{h_{u}^{(k-1)}, \forall u \in \mathcal{N}(v) \cup\{v\}\right\}\right) hv(k)=ReLU(W⋅MEAN{hu(k−1),∀u∈N(v)∪{v}})(3)
2.3 两类任务
文中有两类任务:节点分类和图分类。
对于节点分类问题,节点在最后一层的表示 h v ( K ) h_{v}^{(K)} hv(K),就可以用于预测。
对于图分类问题,需要将graph中所有节点特征转变成graph特征,整个图的表示 h G h_G hG:
h G = READOUT ( { h v ( K ) ∣ v ∈ G } ) (4) \tag{4} h_{G}=\operatorname{READOUT}\left(\left\{h_{v}^{(K)} | v \in G\right\}\right) hG=READOUT({hv(K)∣v∈G})(4)
READOUT表示一个置换不变性函数(permutation invariant function),也可以是一个图级pooling函数,可参考
- Hierarchical graph representation learning with differentiable pooling,NIPS 2018
- An end-to-end deep learning architecture for graph classification,AAAI 2018
2.3 Weisfeiler-Lehman test 图同构测试
图的同构测试问题就是判断两个图的拓扑结构是否等价。这是一个非常有挑战的问题,到目前为止,没有一个线性时间内可以解决的算法。除了一些极端情况(Cai等人,1992),Weisfeler-Lehman (WL)图同构测试是一种有效的、计算效率高的方法,它可以区分很多类图。它的一维形式“naïve vertex refinement”类似于GNNs中的邻居聚合。
Weisfeler-Lehman迭代进行以下操作得到节点新标签以判断同构性:
- 聚合方案:聚合每个节点邻域和自身标签。
- 更新节点标签:使用Hash映射节点聚合标签,作为节点新标签。
例如如下图经过两次迭代后,可以由以节点1为根节点的子树来表示节点1新标签

再看一个WL test的例子

- (a)网络中每个节点有一个label,如图中的彩色的1,2,3,4,5
- (b)标签扩展:做一阶广度优先搜索,即只遍历自己的邻居。比如在图(a)网络G中原(5)号节点,变成(5,234),这是因为原(5)节点的一阶邻居有2,3和4
- (c)标签压缩:仅仅只是把扩展标签映射成一个新标签,如 5,234 => 13
- (d)压缩标签替换扩展标签
- (e)数标签:比如在G网络中,含有1号标签2个,那么第一个数字就是2。这些标签的个数作为整个网络的新特征
WL test的复杂度是O(hm),其中h为iteration次数,m是一次iteration里multiset的个数。
这段解释来自论文:Weisfeiler-Lehman Graph Kernels(作者Shervashidze等人,2011)
Shervashidze等人在WL的基础上提出了度量图之间相似性的WL subtree kernel。即使用WL测试中不同迭代的节点标签的数量作为图的特征向量。
WL测试第k次迭代后节点的标签可以用以高度为k的子树来表示(如图1)。

- 中间图:表示有根的子树结构,WL测试使用它来区分不同的图
- 右图:如果GNN的聚合函数捕获了邻居的full multiset,那么GNN可以以递归的方式捕获有根的子树,其功能与WL测试一样强大
- 上图中蓝色节点进行2次WL测试后的标签可以用以蓝色节点为根节点的2层子树来表示
3 WL test 是GNN性能的上限
Lemma 2
令两个图 G 1 G_1 G1和 G 2 G_2 G2是任意两个非同构的图。如果存在一个图神经网络: A : G → R d \mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d} A:G→Rd将图 G 1 G_1 G1和 G 2 G_2 G2映射到不同的embedding。那么通过图
Weisfeiler-Lehman同构测试也可以确定图 G 1 G_1 G1和 G 2 G_2 G2是非同构的。
证明过程在文中的附录部分。也就是说一个基于图的GNN区分不同的图的能力至多有图
Weisfeiler-Lehman同构测试那么强大。
4 什么样的GNN 可以和WL test 一样强大?
由定理2可知存在这样一个问题,是否存在一种GNNs与WL测试一样强大?在定理3中,答案是肯定的:如果邻居Aggregate函数和Readout函数是单射的,那么得到的GNN与WL测试一样强大。
Theorem 3
令 A : G → R d \mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d} A:G→Rd是一个GNN。对于两个通过Weisfeiler-Lehman同构测试测定为不同构的两个图 G 1 G_1 G1和 G 2 G_2 G2,在GNN层足够多的情况下,如果下面的情况成立,则通过GNN可以将这两个图映射到不同的embedding:
(1) A \mathcal{A} A用下面的公式迭代的聚合和更新节点特征:
h v ( k ) = ϕ ( h v ( k − 1 ) , f ( { h u ( k − 1 ) : u ∈ N ( v ) } ) ) (5) \tag{5} h_{v}^{(k)}=\phi\left(h_{v}^{(k-1)}, f\left(\left\{h_{u}^{(k-1)}: u \in \mathcal{N}(v)\right\}\right)\right) hv(k)=ϕ(hv(k−1),f({hu(k−1):u∈N(v)}))(5)
- 函数 f f f作用在multisets上
- ϕ \phi ϕ函数时单射的(injective)
证明过程在文中的附录部分。
接下来,使用这个推理来构建一个功能最强大的GNN。后面部分还研究了目前主流的GNN变体,发现它们的聚合方案本质上不是单射的,因此功能更弱,但是它们可以捕获图的其他有趣特征。
5 构建一个强大的图神经网络GIN
为了研究GNN的表示能力,可以分析GNN将两个节点映射到embedding空间的同一位置时的表示能力,所以可以将分析简化为这样一个问题:GNN是否可以将不同的图结构映射(即两个multisets)到相同的embedding。这种将任意两个不同的图映射到不同embedding的能力意味着要解决具有挑战性的图同构问题。也就是说,希望同构图的embedding相同,非同构图的embedding不同。一个强大的GNN不会将两个不同的邻域映射到相同的表示,这意味着它的聚合模式必须是单射的(injective)。因此,文中将一个GNN的聚合方案抽象为一类神经网络可以表示的multisets上函数。
除了区分不同的图之外,GNN还有一个值得讨论的重要优点,即捕获图结构的相似性。WL测试中的节点特征向量本质上是one-hot编码,因此不能捕获子树之间的相似性。相反,满足定理3的GNN通过学习将子树嵌入到低维空间来推广WL测试。这使得GNN不仅能够区分不同的结构,而且还能够学习将类似的图结构映射到类似的 embeddings,并捕获图结构之间的依赖关系。
5.1 Graph Isomorphism Network (GIN) 图同构网络
文中提出了一个网络架构,Graph Isomorphism Network (GIN) 图同构网络,这个网络满足Theorem 3的条件。该模型对WL测试进行了推广,从而在GNNs中鉴别能力最强。
作者接着证明提出定理5和推论6,当X为可数时,将aggregate设置为sum, combine 设置为 1 + ϵ 1+\epsilon 1+ϵ时,会存在 f ( x ) f(x) f(x),使 h ( c , X ) h(c,X) h(c,X)为单射:
h ( c , X ) = ( 1 + ϵ ) ⋅ f ( c ) + ∑ x ∈ X f ( x ) h(c, X)=(1+\epsilon) \cdot f(c)+\sum_{x \in X} f(x) h(c,X)=(1+ϵ)⋅f(c)+x∈X∑f(x)
- c为节点自身特征, X为邻域特征集
进一步推出任意 g ( c , X ) g(c, X) g(c,X)都可以分解成以下 f ∘ φ f \circ \varphi f∘φ形式,满足单射性
g ( c , X ) = φ ( ( 1 + ϵ ) ⋅ f ( c ) + ∑ x ∈ X f ( x ) ) g(c, X)=\varphi\left((1+\epsilon) \cdot f(c)+\sum_{x \in X} f(x)\right) g(c,X)=φ((1+ϵ)⋅f(c)+x∈X∑f(x))
通过引入多层感知机MLP,去学习 φ \varphi φ和 f f f,保证单射性。最终得到基于MLP+SUM的GIN框架:
h v ( k ) = MLP ( k ) ( ( 1 + ϵ ( k ) ) ⋅ h v ( k − 1 ) + ∑ u ∈ N ( v ) h u ( k − 1 ) ) (6) \tag{6} h_{v}^{(k)}=\operatorname{MLP}^{(k)}\left(\left(1+\epsilon^{(k)}\right) \cdot h_{v}^{(k-1)}+\sum_{u \in \mathcal{N}(v)} h_{u}^{(k-1)}\right) hv(k)=MLP(k)⎝⎛(1+ϵ(k))⋅hv(k−1)+u∈N(v)∑hu(k−1)⎠⎞(6)
- MLP可以近似拟合任意函数,故可以学习到单射函数,而graphsage和gcn中使用的单层感知机不能满足。
- 约束输入特征是one-hot,故第一次迭代sum后还是满足单射性,不需先做MLP的预处理。
- 根据定理4, 迭代一轮得到新特征 h v ( k ) h_{v}^{(k)} hv(k)是可数的、经过了 转换 f ( x ) f(x) f(x)(隐),下一轮迭代还是满足单射性条件。
5.2 Graph-level Readout of GIN
通过GIN学习的节点embeddings可以用于类似于节点分类、连接预测这样的任务。对于图分类任务,文中提出了一个“readout”函数:给定独立的节点的embeddings,生成整个图的embedding。
Readout模块使用 concat+sum,对每次迭代得到的所有节点特征求和得到图的特征,然后拼接起来。
h G = CONCAT ( READOUT ( { h v ( k ) ∣ v ∈ G } ) ∣ k = 0 , 1 , … , K ) (7) \tag{7} h_{G}=\operatorname{CONCAT}\left(\operatorname{READOUT}\left(\left\{h_{v}^{(k)} | v \in G\right\}\right) | k=0,1, \ldots, K\right) hG=CONCAT(READOUT({hv(k)∣v∈G})∣k=0,1,…,K)(7)
h G = CONCAT ( sum ( { h v ( k ) ∣ v ∈ G } ) ∣ k = 0 , 1 , … , K ) h_{G}=\operatorname{CONCAT}\left(\operatorname{sum}\left(\left\{h_{v}^{(k)} | v \in G\right\}\right) | k=0,1, \ldots, K\right) hG=CONCAT(sum({hv(k)∣v∈G})∣k=0,1,…,K)
6 为何基于mean、max aggregate的GNN不够强大?
6.1 mean和max 无法区分哪些结构
节点 v v v和 v ′ v' v′为中心节点,通过聚合邻居特征生成embeddind,分析不同aggregate设置下是否能区分不同的结构(如果能捕获不同结构,二者的embedding应该不一样)。

- 设红绿蓝色节点特征值分别为r,g,b,不考虑combine
图a
- mean:左 1 2 ( b + b ) = b \frac{1}{2}(b+b)=b 21(b+b)=b, 右: 1 3 ( b + b + b ) = b \frac{1}{3}(b+b+b)=b 31(b+b+b)=b, 无法区分。
- max:左 b b b ,右 b b b 无法区分
- sum:左 2 b 2b 2b, 右 3 b 3b 3b, 可以区分。
图b
- mean:左 1 2 ( r + g ) \frac{1}{2}(r+g) 21(r+g), 右: 1 3 ( g + 2 r ) \frac{1}{3}(g+2r) 31(g+2r), 可以区分。
- max:左 m a x ( r , g ) max(r,g) max(r,g), 右: m a x ( g , r , r ) max(g,r,r) max(g,r,r), 无法区分。
- sum:左 r + g r+g r+g, 右 2 r + g 2r+g 2r+g, 可以区分。
图c
- mean:左 1 2 ( r + g ) \frac{1}{2}(r+g) 21(r+g), 右: 1 4 ( 2 r + 2 g ) \frac{1}{4}(2r+2g) 41(2r+2g), 无法区分。
- max:左 m a x ( g , g , r , r ) max(g,g,r,r) max(g,g,r,r), 右: m a x ( r , g ) max(r,g) max(r,g), 无法区分。
- sum:左 r + g r+g r+g, 右 2 r + 2 g 2r+2g 2r+2g , 可以区分。
结论:由于mean和max-pooling 函数 不满足单射性,无法区分某些结构的图,故性能会比sum差一点。
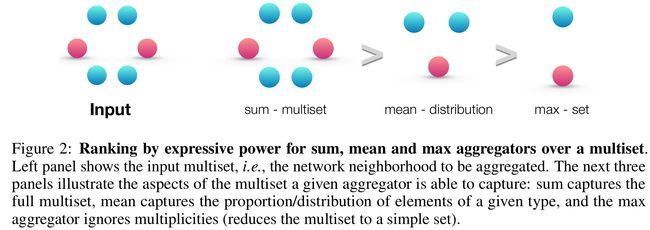
6.2 sum, mean, max 分别可以捕获什么信息?
三种不同的aggregate
- sum:学习全部的标签以及数量,可以学习精确的结构信息
- mean:学习标签的比例(比如两个图标签比例相同,但是节点有倍数关系),偏向学习分布信息
- max:学习最大标签,忽略多样,偏向学习有代表性的元素信息
7 实验
Datasets
9个图分类benchmarks
4个生物信息学数据集
- MUTAG
- PTC
- NCI1
- PROTEINS
5个社交网络数据集
- OLLAB
- IMDB-BINARY
- IMDB-MULTI
- REDDIT-BINARY
- REDDIT-MULTI5K
Baselines
拟合能力——train效果

关注泛化能力——test集效果
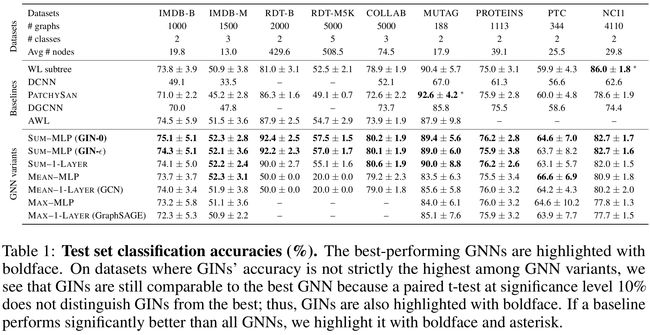
- GIN-0 比GIN-eps 泛化能力强:可能是因为更简单的缘故
- GIN 比 WL test 效果好:因为GIN进一步考虑了结构相似性,即WL test 最终是one-hot输出,而GIN是将WL test映射到低维的embedding
- max在 无节点特征的图(用度来表示特征)基本无效
8 讨论
本文主要基于对 graph分类,证明了 sum 比 mean 、max 效果好,但是不能说明在node 分类上也是这样的效果,另外可能优先场景会更关注邻域特征分布,或者代表性, 故需要都加入进来实验。