如何理解傅立叶级数公式？

1. 对周期函数进行分解的猜想

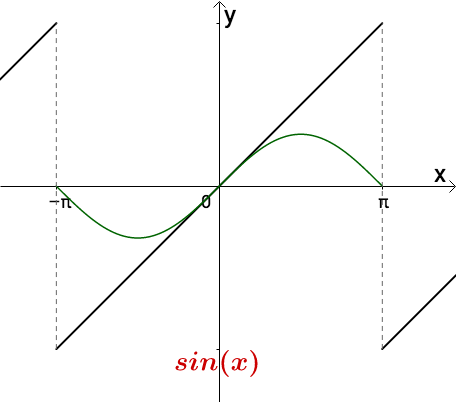
拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示，比如下图中，黑色的斜线就是周期为$2\pi$的函数，而红色的曲线是三角函数之和，可以看出两者确实近似：

而另外一位数学家,让·巴普蒂斯·约瑟夫·傅里叶男爵（1768－1830）猜测任意周期函数都可以写成三角函数之和。

2. 分解的思路

假设f(x)是周期为T的函数，傅里叶男爵会怎么构造三角函数的和，使之等于f(x)？

2.1 常数项

对于$y=C,C\in \mathbb{R}$这样的常数函数：

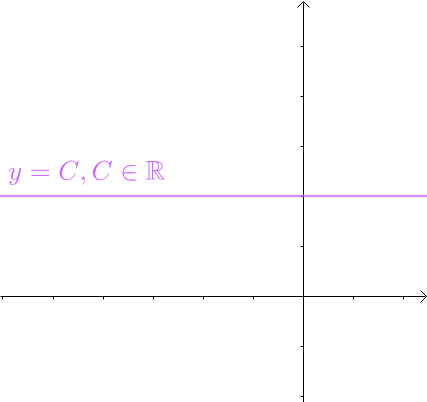
根据周期函数的定义，常数函数是周期函数，周期为任意实数。
所以，分解里面得有一个常数项。

2.2 通过sin(x),cos(x)进行分解

首先，sin(x),cos(x)是周期函数，进行合理的加减组合，结果可以是周期函数。
其次，它们的微分和积分都很简单。
然后，sin(x)是奇函数，即：
-sin(x)=sin(-x)
从图像上也可以看出，sin(x)关于原点对称，是奇函数：

而奇函数与奇函数加减只能得到奇函数。

而cos(x)是偶函数，即：
cos(x)=cos(-x)
从图像上也可以看出，cos(x)关于Y轴对称，是偶函数：

同样的，偶函数与偶函数加减只能得到偶函数。

但是任意函数可以分解为奇偶函数之和：

$$f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}=f_{even}+f_{odd}$$
所以同时需要sin(x),cos(x)。

2.3 保证组合出来周期为T

之前说了，f(x)是周期为T的函数，我们怎么保证组合出来的函数周期依然为T呢？
比如下面这个函数的周期为$2\pi$：

很显然，sin(x)的周期也是$2\pi$：

sin(2x)的周期也是$2\pi$，虽然最小周期是$\pi$：

很显然，$sin(nx),n\in \mathbb{N}$的周期都是$2\pi$：

更一般的，如果f(x)的周期为T，那么：

$$sin(\frac{2\pi n}{T}x)cos(\frac{2\pi n}{T}x),n\in \mathbb{N}$$

这些函数的周期都为T。
将这些函数进行加减，就保证了得到的函数的周期也为T。

2.4 调整振幅

现在我们有一堆周期为$2\pi$的函数了，比如说

$$sin(x),sin(2x),sin(3x),sin(4x),sin(5x)$$

现在，sin(x)看起来处处都比目标函数低一些：

通过调整振幅可以让它们慢慢接近目标函数，比如把它的振幅增加一倍：

2sin(x)有的地方超出去了，从周期为$2\pi$的函数中选择一个，减去一点：

调整振幅，加加减减，我们可以慢慢接近目标函数：

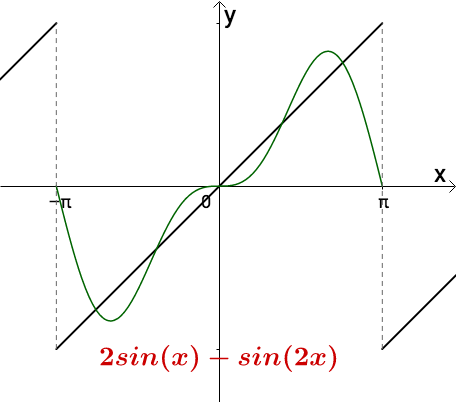
综上，构造出来的三角函数之和大概类似下面的样子：

$$f(x)=C+\sum _{n=1}^{\infty }\left(a_{n}cos(\frac{2\pi n}{T}x)+b_{n}sin(\frac{2\pi n}{T}x)\right),C\in \mathbb{R}$$

这样就符合之前的分析：

• 有常数项
• 奇函数和偶函数可以组合出任意函数
• 周期为T
• 调整振幅，逼近原函数

之前的分析还比较简单，后面开始有点难度了。即怎么确定这三个系数：

$$C{a}_n{b}_n$$

3. sin(x)的另外一种表示方法

直接不好确定，要迂回一下，先稍微介绍一下什么是：$e^{i\omega t}$？

3.1 $e^{i\omega t}$

看到复数也不要怕，根据之前的文章如何通俗易懂地解释欧拉公式，看到类似于$e^{i\theta }$这种就应该想到复平面上的一个夹角为$\theta$的向量：

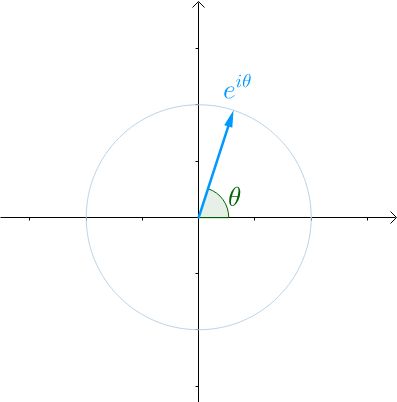
那么当$\theta$不再是常数，而是代表时间的变量t的时候：

$$e^{i\theta }\to e^{it}$$

随着时间t的流逝，从0开始增长，这个向量就会旋转起来，$2\pi$秒会旋转一圈，也就是$T=2\pi$：

3.2 通过$e^{i\omega t}$表示sin(t)

根据欧拉公式，有：

$$e^{it}=cos(t)+isin(t)$$

所以，在时间t轴上，把$e^{it}$向量的虚部（也就是纵坐标）记录下来，得到的就是sin(t)：

在时间t轴上，把$e^{i2t}$向量的虚部记录下来，得到的就是sin(2t)：

如果在时间t轴上，把$e^{it}$的实部（横坐标）记录下来，得到的就是cos(t)的曲线：

更一般的,具有两种看待sin(x),cos(x)的角度：

$$e^{i\omega t}⟺\{\begin{array}{l}sin(\omega t)\\ cos(\omega t)\end{array}$$

这两种角度，一个可以观察到旋转的频率，所以称为频域；一个可以看到流逝的时间，所以称为时域：

4. 通过频域来求系数

4.1 函数是线性组合

假设有这么个函数：

$$g(x)=sin(x)+sin(2x)$$

是一个$T=2\pi$的函数：

如果转到频域去，那么它们是下面这个复数函数的虚部：

$$e^{it}+e^{i2t}$$

先看看$e^{i\theta }+e^{i2\theta }$，其中$\theta$是常数，很显然这是两个向量之和：

现在让它们动起来，把$\theta$变成流逝的时间t，并且把虚部记录下来：

我们令：

$$G(t)=e^{it}+e^{i2t}$$

这里用大写的G来表示复数函数。
刚才看到了，$e^{it}$和$e^{i2t}$都是向量，所以上式可以写作：

$$G(t)=e^{it}+e^{i2t}$$

这里就是理解的重点了，从线性代数的角度：

• $e^{it}$和$e^{i2t}$是基（可以参考无限维的希尔伯特空间）
• G(t)是基$e^{it}$和$e^{i2t}$的线性组合

g(t)是G(t)的虚部，所以取虚部，很容易得到：

$$g(t)=sin(t)+sin(2t)$$

即g(t)是基sin(t),sin(2t)的线性组合。
那么sin(t),sin(2t)的系数，实际上是g(t)在基sin(t),sin(2t)下的坐标了。

4.2 如何求正交基的坐标

有了这个结论之后，我们如何求坐标？
我们来看个例子，假设：

$$w_{}=3u_{}+2v_{}$$

其中

$$w_{}=\left(\begin{array}{c}1\\ 5\end{array}\right),u_{}=\left(\begin{array}{c}1\\ 1\end{array}\right),v_{}=\left(\begin{array}{c}-1\\ 1\end{array}\right)$$
通过点积：

$$u_{}\cdot v_{}=0$$

可知这两个向量正交，是正交基。

通过点积可以算出$v_{}$的系数（对于正交基才可以这么做）：

$$\frac{w_{}\cdot v_{}}{v_{}\cdot v_{}}=\frac{(1,5)\cdot (-1,1)}{(-1,1)\cdot (-1,1)}=2$$

如何求sin(nt)基下的坐标

在这里抛出一个结论（可以参考无限维的希尔伯特空间），函数向量的点积是这么定义的：

$$f(x)\cdot g(x)={\int }_0^{T}f(x)g(x)dx$$

其中，f(x)是函数向量，g(x)是基，T是f(x)的周期。
那么对于：
$$g(x)=sin(x)+sin(2x)$$
其中，g(x)是向量，sin(t),sin(2t)是基，周期$T=2\pi$。
根据刚才内积的定义：

$$sin(t)\cdot sin(2t)={\int }_0^{2\pi }sin(t)sin(2t)dt=0$$

所以是正交基，那么根据刚才的分析，可以这么求坐标：

$$\frac{g_{}\cdot sin(t)}{sin(t)\cdot sin(t)}=\frac{{\int }_0^{2\pi }g(x)sin(x)dx}{{\int }_0^{2\pi }si{n}^2(x)dx}=1$$

4.4 更一般的

对于我们之前的假设，其中f(x)周期为T：

$$f(x)=C+\sum _{n=1}^{\infty }\left(a_{n}cos(\frac{2\pi n}{T}x)+b_{n}sin(\frac{2\pi n}{T}x)\right),C\in \mathbb{R}$$

可以改写为这样：

$$f(x)=C\cdot 1+\sum _{n=1}^{\infty }\left(a_{n}cos(\frac{2\pi n}{T}x)+b_{n}sin(\frac{2\pi n}{T}x)\right),C\in \mathbb{R}$$

也就是说向量f(x)的基为：

$$\{1,cos(\frac{2\pi n}{T}x),sin(\frac{2\pi n}{T}x)\}$$

是的，1也是基。结合偶函数*奇函数=奇函数的性质可以计算出$a_n,b_n$:

$$\begin{gathered} a_n=\frac{{\int }_0^{T}f(x)cos(\frac{2\pi n}{T}x)dx}{{\int }_0^{T}co{s}^2(\frac{2\pi n}{T}x)dx}=\frac{2}{T}{\int }_0^{T}f(x)cos(\frac{2\pi n}{T}x)dx \\ {b}_n=\frac{{\int }_0^{T}f(x)sin(\frac{2\pi n}{T}x)dx}{{\int }_0^{T}si{n}^2(\frac{2\pi n}{T}x)dx}=\frac{2}{T}{\int }_0^{T}f(x)sin(\frac{2\pi n}{T}x)dx \end{gathered}$$

C也可以通过点积来表示，最终我们得到：

$$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos (\frac{2\pi nx}{T})+b_n\sin (\frac{2\pi nx}{T})\right)$$

其中：

$$\begin{gathered} a_n=\frac{2}{T}{\int }_{x_0}^{x_0+T}f(x)\cdot \cos (\frac{2\pi nx}{T})dx,n\in \{0\}\bigcup \mathbb{N} \\ {b}_n=\frac{2}{T}{\int }_{x_0}^{x_0+T}f(x)\cdot \sin (\frac{2\pi nx}{T})dx,n\in \mathbb{N} \end{gathered}$$

5. 傅立叶级数的另外一种表现形式

利用欧拉公式$e^{ix}=\cos x+i\sin x$，我们发$\cos x,\sin x$可表示成

$$\cos x=\frac{e^{ix}+e^{-ix}}{2},\sin x=\frac{e^{ix}-e^{-ix}}{2i}$$
再将傅立叶级数f(x)中$\cos (\frac{2\pi n}{T}x)$和$\sin (\frac{2\pi n}{T}x)$的线性组合式改写如下：

$$\begin{array}{rl}{a}_n\cos (\frac{2\pi n}{T}x)+b_n\sin (\frac{2\pi n}{T}x)& =a_n\left(\frac{e^{i\frac{2\pi n}{T}x}+e^{-i\frac{2\pi n}{T}x}}{2}\right)+b_n\left(\frac{e^{i\frac{2\pi n}{T}x}-e^{-i\frac{2\pi n}{T}x}}{2i}\right)\\ & =\left(\frac{a_n-i{b}_n}{2}\right)e^{i\frac{2\pi n}{T}x}+\left(\frac{a_n+i{b}_n}{2}\right)e^{-i\frac{2\pi n}{T}x}\\ & =c_n{e}^{i\frac{2\pi n}{T}x}+c_{-n}{e}^{-i\frac{2\pi n}{T}x}\end{array}$$
可以验证

$$\begin{gathered} c_{-n}=\frac{a_{-n}-i{b}_{-n}}{2}=\frac{a_n+i{b}_n}{2} \\ {c}_n=\frac{a_n-i{b}_n}{2} \end{gathered}$$
这是因为$a_n$是一个偶函数，$b_n$是一个奇函数。此外，若n=0，就有$c_0=a_0/2$。将以上结果代回f(x)的傅立叶级数即得傅立叶级数指数形式：

$$f(x)=\sum _{n=-\infty }^{\infty }\underset{\text{基的坐标}}{c_n}\cdot \underset{\text{正交基}}{e^{i\frac{2\pi nx}{T}}}$$
将$a_n,b_n$的结果代进去可以得到
$$c_n=\frac{1}{T}{\int }_{-T/2}^{T/2}f(x)(\cos (\frac{2\pi n}{T}x)-i\sin (\frac{2\pi n}{T}x))dx=\frac{1}{T}{\int }_{-T/2}^{T/2}f(x)e^{-i\frac{2\pi n}{T}}xdx$$
公式用频率替换：$\Delta \omega =\frac{2\pi }{T}$,再令${\omega }_n=\omega n$现在我们可以写出全新的傅里叶级数：

$$f(x)=\sum _{n=-\infty }^{\infty }\frac{\Delta \omega }{2\pi }{\int }_{-T/2}^{T/2}f(x)e^{-i\omega nx}dx\cdot e^{i\omega nx}=\sum _{n=-\infty }^{\infty }\frac{\Delta \omega }{2\pi }{\int }_{-T/2}^{T/2}f(x)e^{-i{\omega }_{n}x}dx\cdot e^{i{\omega }_{n}x}$$

现在令$T\to \infty ，\Delta \omega \to 0$，并设

$$F(\omega )={\int }_{-\infty }^{+\infty }f(x)e^{-i\omega x}dx$$

$$\begin{array}{rl}f(x)& =\sum _{n=-\infty }^{\infty }\frac{\Delta \omega }{2\pi }F({\omega }_n)\cdot e^{i{\omega }_{n}x}\\ & =\frac{1}{2\pi }\sum _{n=-\infty }^{\infty }F({\omega }_n)\cdot e^{i{\omega }_{n}x}\Delta \omega \\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(\omega )\cdot e^{i\omega x}d\omega \end{array}$$
于是得到了傅里叶变换就是

$$F(\omega )={\int }_{-\infty }^{+\infty }f(x)e^{-i\omega x}dx$$