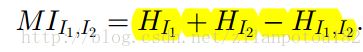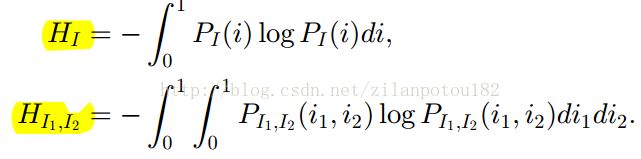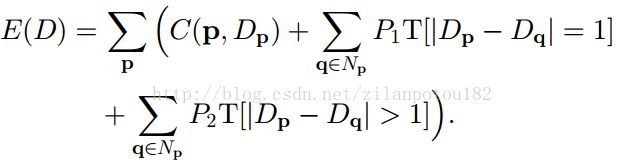Semi-Global Matching（SGM）算法原文理解

  参考：@迷雾forest http://blog.csdn.net/wsj998689aa/article/details/49464017，原博主对SGM算法的精髓理解的很透，我是在参考他文章的基础上，才能看懂SGM算法几处关键的地方。本文的不同在于加入了一些我自己的理解，并且调整了一下整个算法阐述的思路，当是自己的一个阅读笔记。后边打算再做一下SGM原始算法与OpenCV的SGBM算法实现的对比，并且争取自己实现一下SGM算法。因为我的导师不搞这个方向，很多东西都是我自己的理解，恐怕会有不对的地方，还请大家多指正。下面直接从第二章开始。

2.半全局立体匹配

  半全局立体匹配算法基于一种逐像素匹配的方法，该方法使用互信息来评价匹配代价，并通过组合很多一维的约束来近似一个全局的二维平滑约束。本方法分成下面几个步骤，其中有一些并不是必须的。

2.1 逐像素匹配代价的计算

  输入的左右图像必须已经知道对极几何模型，但是不一定是校正过的，因为有些图像是难以校正的，比如推扫式图像。要计算参考图（base image）某点P的匹配代价，需要用到其灰度为I_bp，及在待匹配图（match image）的疑似匹配点q，其灰度为I_mq，p和q之间有极线方程q=ebm(p,d)，d是极线的参数。如果图像已经被校正了，那么待匹配图在参考图的右边，且d代表视差。

  一个重要的问题是用于匹配的区域的大小和形状，区域越大，鲁棒性越好，但是大了以后会导致物体的边界模糊。这里不使用P邻域内的视差是连续的这一假设，也就是说，只有I_bp和I_mq这两个灰度值被用来计算点p匹配代价，其他的点不考虑。

  文章介绍一种逐像素匹配代价计算的方法是Brichfield and Tomasi提出的基于采样的方法《Depth Discontinuities by Pixel-to-Pixel Stereo》，该方法在OpenCV SGBM算法中使用。但是这里，文章使用了新的方法，即基于互信息的匹配代价，该方法对光照不敏感。下面介绍互信息。

  互信息M的定义式，互信息是基于熵来计算的，下面的三项分别是图1的熵，图2的熵，以及图12的联合熵，紧接着给出熵和联合熵的定义：

                                                                                 

                                                       

                                                                        

  什么是熵？参考@迷雾forest：先说说熵，熵是用来表征随机变量的不确定性（可以理解为变量的信息量），不确定性越强那么熵的值越大（最大为1），那么图像的熵其实就代表图像的信息量。互信息度量的是两个随机变量之间的相关性，相关性越大，那么互信息就越大。可以想想看，两幅图像如果匹配程度非常高，说明这两幅图像相关性大还是小？显然是大，知道一幅图像，另外一幅图像马上就知道了，相关性已经不能再大了！！！反之，如果两幅图像配准程度很低，那么两幅图像的互信息就会非常小。所以，立体匹配的目的当然就是互信息最大化。这就是为什么使用互信息的原因。

  此时，为了计算互信息，就要先计算熵，而根据上的定义式，为了计算H_I和H_I1I2，首先需要知道P_I和P_I1I2是啥，其中P_I代表某个点i的概率分布，也就是灰度直方图中灰度为i的点出现的概率。P_I1I2是二维概率分布，二维概率分布是什么意思呢，比如现在左图是100*100，则一共有10000个像素点，对于左图中的每一个点p，它在左图的灰度值为i，它在右图的对应点的灰度值为j，它们构成一个点对（i,j），此时点对（i，j）对应的计数加1；然后遍历其他所有点，如果某个点对出现过，就把该点对对应的计数值加1，最后把所有点对的计数值除以10000，就得到某个点对（i,j）的概率。不难理解，因为i和j的范围都是0-255，所以这个二维概率分布图P_I1I2的尺寸为256*256。

 现在知道了P_I和P_I1I2，就要返回去计算H_I和H_I1I2。对于H_I1I2，作者根据Kim等人的成果，直接用泰勒展开式，把原来的联合熵公式转换为下面这个：

                   

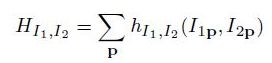
  也就是各像素点对应的h值之和的形式，那么h_I1I2又是什么呢？h_I1I2是根据P_I1I2来计算的，其公式是：

           

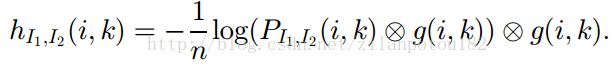
  也就是说，得到二维概率分布图（其尺寸永远是256*256），然后与高斯核进行卷积，然后求log，然后再卷积，就得到这个h_I1I2，其实它也是个256*256的图，这样就可以建一个256*256的表，然后H_I1I2的解释就是，对于逐个点p，其左图像中灰度值为I_1P，右图像灰度值为I_2p，则其对应的h_I1I2可以直接查表得出，然后整个图的H_I1I2就是把所有点p的h_I1I2加起来。

  这里列出由两个图得到h_I1I2的过程，这里有一个warp，它的意思是，在求二维概率分布之前，要根据一个初始的视差图，对待匹配图像进行修正，修正后，左图中某一点大概率能有一个正确的对应点，则此时两个点的灰度值基本相同，这样就使得（5,5）（10,10）这样的点对占大多数，所以P的图像基本是一个45度的直线。但是这个作为参考的视差图是粗糙的，它是怎么得到的作者没有提到，只知道遮挡点的视差都被设为0，只有非遮挡点才有视差，用这样粗糙的视差图作为参考去对待匹配图像做修正，就可能使对应点的视差不一致，因此就会出现不在45°线上的情况，这就需要高斯模糊来去躁了。至此，就讨论完了H_I1I2的计算。还有HI1和HI2。  

  对于H_I，其计算方法本来跟H_I1I2是不同的。但是这里有个问题，如果考虑遮挡的问题，那么有些点根本没有可以匹配的点，那么这些点不应该被考虑，为此，我们又一次想到联合熵，联合熵是基于联合概率分布的，其基于的点都可以保证是匹配点，因此，这里考虑对于H_I的计算，也使用H_I1I2即联合熵的求法。公式如下：

          

  这里h_I的计算就跟上面很相似了，需要注意的是计算P的时候不要把遮挡点统计进来。

  最后，互信息MI的最终定义就是：

          

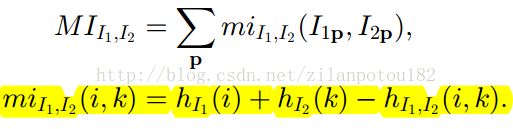
  相应的，基于互信息的某点p的匹配代价CMI就是：

           

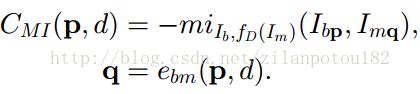
  这就是说，计算某一点的匹配代价，就是先根据极线方程求出在右图像中的灰度，根据这两个点的灰度构成的灰度值对直接在互信息图M中查找，然后取负。

  这里还有一个问题，求互信息之前要对待匹配图像进行校正，根据Kim等，采用一个迭代的过程，一开始采用一个随机的视差图来进行第一次的互信息计算，然后根据这个互信息就可以得到新的视差图，再根据这个视差图再求互信息，如此迭代，一般也不要太多次数，比如3次可以。为什么可以这么“随意”，因为像素点很多，所以即使随机生成的视差图有错误，体现在概率分布上也没有特别大的影响。

  最后就是分层互信息。既然一个粗糙的初始视差图也可以得到较精准的概率分布，那么在前面的迭代中可以使用一个基于相关的快速方法，并且只在最后一次迭代时使用更精准和耗时的方法。下面就介绍这种方法，也就是分层互信息法（HMI）。

  用HMI来计算匹配代价，该方法递归的使用降采样过的参考图和待匹配图，采样率是1/2，然后得到的视差图的长宽也是上一幅视差图的一半（注意，因为我们只对图像降采样，而图像上的点仍然是可能占满0-255空间的，因此概率分布图仍然是256*256）。那么如果迭代四次，第一次使用的是1/16的图，下一次是1/8，再1/4和1/2，最后一次是1，这就得到较高精度的匹配代价。单次迭代的时间复杂度是O(WHD)，所以总的运算时间是 ，可见复杂度并不是很高，之比BT算法多了14%。注意低一层的图只作为下一层的输入，而不作为最后结果的输入。上面的公式中为啥要乘3，根据@迷雾forest，乘以3的原因是随机生成的视差图十分不靠谱，需要反复迭代3次才能得到同样分辨率下的靠谱视差图，然后再参与后续高分辨率的计算。

2.2 代价聚合

  由2.1已经得到基于互信息的匹配代价，但是这个逐像素的匹配代价容易受到误匹配和噪声点的影响，因此这里还要考虑使用某点的邻域视差数据来构造惩罚函数以增加平滑性约束。也就是说，把代价聚合里面加入平滑性约束的考虑，也就是设计一个全局的能量函数E(D)，用它来综合匹配代价和平滑性约束。能量函数的定义式如下：

    

  （注意这里惩罚值的意义，惩罚就代表着不想选这种情况，如果有一个视差图它的惩罚值比另一幅大，那么就不选这个，也就是通过惩罚筛掉了我们不想要的情况，这个弯要转过来）

  式中第一项是基于互信息的代价计算项；后两项是当前像素p和其邻域N_p内所有像素q之间的约束，如果p和q的视差只差1，那么惩罚P1，否则惩罚系数P2，P2要大于P1。如果当前点和邻域点的差值比较小，就选择一个小的惩罚值，这么做保证可以对斜面和曲面有一定的适应性（也就是说不是完全要筛掉它们，而是还有容忍）。

  现在问题就变成找到一个视差图，它能使这个全局的能量函数最小。关于求这个视差图的方法，@迷雾forest文章说的讲比较清楚：这个时候问题来了，这个E对p是不可导的，这意味着我们常看到的梯度下降，牛顿高斯等等算法在这里都不适用，作者于是采用了动态规划来解决这一问题。简单地说，p的代价想要最小，那么前提必须是邻域内的点q的代价最小，q想要代价最小，那么必须保证q的领域点m的代价最小，如此传递下去。怎么利用动态规划来求解E，其实这个求解问题是NP完全问题，想在2D图像上直接利用动态规划求解是不可能的，只有沿着每一行或者每一列求解才能够满足多项式时间，但是这里问题来了，如果我们只沿着每一行求解，那么行间的约束完全考虑不到，q是p的领域的点其实这个时候被弱化到了q是p的左侧点或者右侧点，这样的求优效果肯定很差。于是，大招来了！！我们索性不要只沿着横或者纵来进行优化，而是沿着一圈8个或者16个方向进行优化。

  什么叫“沿着一圈8个或者16个方向进行优化”呢，结合下面的执行步骤详细解释。现在可以采用一种新的匹配代价聚合方法，它使用某点p上邻域内所有方向上的代价构成一维的DP问题。S(p,d)代表某一点（像素点名p，视差值d）的代价聚合值，它的求法是，所以Lr是什么？以p为中心，可以找到16个（或8个，下同）邻域方向，然后在每个邻域方向上有一个指向p的矢量，而r表示16个矢量中的某一个。因此Lr就是代表当前矢量路径r上的代价聚合值。所以，S（p,d）就是把16个代价聚合值相加，而这16个又都是各自路径上的最小代价。所以求出来的S(p,d)就是p点的最小代价。注意r是一条路，它只能是这个方向，但是长度可以延长。也就是说，16个方向分别算到底。那么下面就是考虑，Lr(p,d)到底如何计算呢。且看下式：

          

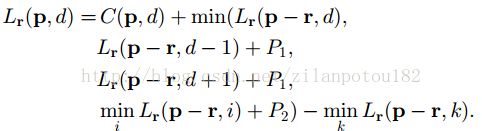
  P点上某个邻域方向的代价聚合值分为三项，第一是当前点的匹配代价，就是前面的C_MI；第二项是min（当前邻域方向上p-r这个像素点的当前视差代价聚合值，p-r点的视差差值为1的代价聚合值 + P1，p-r点的视差插值大于1的最小代价聚合值 + P2）；最后一项是p-r点的视差插值大于1的最小代价聚合值，最后一项是为了防止计算结果太大，做的统一的调整。

  关于这个p-r，它的意义不是很好理解，我的理解的是，因为每次要沿着一个矢量方向算到底，那么p-r就是某个矢量上距离p为一个单位、两个单位等等点，直到算完（addsthe lowest cost of the previous pixel p-r ofthe path）。

  把各个方向上的Lr都求和得到S(p,d)，作者建议方向数最好用16，至少为8，这些方向最好是水平、垂直或位于某对角线上，如果不是，那就多做一步，调整为这三种。

  最后考虑一下计算量和实现方法。作者推荐的是先计算所有点的C(p,d)，然后把值规范化到0-2¹¹的取值范围内。所有的匹配代价都存在C[]数组里面，该数组大小W*H*D，然后用一个与C同样大小的数组S[]来保存代价聚合值。然后对每个点b，计算所有邻域矢量方向上的代价聚合值，计算过程中体现动态规划中记忆化搜索的思想。

2.5 视差求精

  后处理这一块我感觉http://blog.csdn.net/zhubaohua_bupt/article/details/51866567所做的介绍比本文要更详细，因为视差求精本来就是精益求精嘛，所以越全面参考价值越大。

2.6 大尺寸图片的处理

  SGM算法需要保存临时变量包括每个点的匹配代价、聚合代价、融合前的视差图等等，因此中间步骤需要的存储空间非常大，很可能导致空间占满的情况。为此，提出一种方法，把基准图分成片，以片的形式参与到2.1-2.3步的运算，然后再组合起来进行2.4的运算。划分片的时候，它们需要是重叠的，也就是每个片取大一点。这种方法对于大尺寸的照片非常适用。

2.7 视差图融合

  注意这里不是左右视差图的融合，而是针对不同视角获取到的视差图进行融合。我的应用只用了一个视角，所以这里没怎么看。