Codeforces Round #644 (Div. 3)题目+题解+代码（A、B、C、D、E、G）

A. Minimal Square

来源：http://codeforces.com/contest/1360/problem/A

Find the minimum area of a square land on which you can place two identical rectangular a×b houses. The sides of the houses should be parallel to the sides of the desired square land.

Formally,

You are given two identical rectangles with side lengths a and b (1≤a,b≤100) — positive integers (you are given just the sizes, but not their positions).
Find the square of the minimum area that contains both given rectangles. Rectangles can be rotated (both or just one), moved, but the sides of the rectangles should be parallel to the sides of the desired square.
Two rectangles can touch each other (side or corner), but cannot intersect. Rectangles can also touch the sides of the square but must be completely inside it. You can rotate the rectangles. Take a look at the examples for a better understanding.

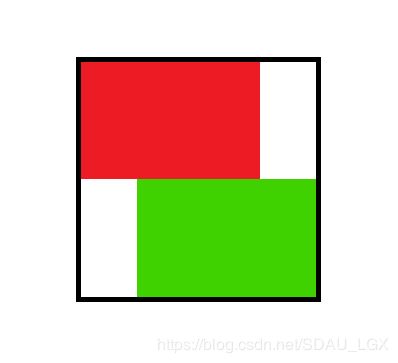
The picture shows a square that contains red and green rectangles.
Input
The first line contains an integer t (1≤t≤10000) —the number of test cases in the input. Then t test cases follow.

Each test case is a line containing two integers a, b (1≤a,b≤100) — side lengths of the rectangles.

Output
Print t answers to the test cases. Each answer must be a single integer — minimal area of square land, that contains two rectangles with dimensions a×b.

Example
inputCopy
8
3 2
4 2
1 1
3 1
4 7
1 3
7 4
100 100

outputCopy
16
16
4
9
64
9
64
40000

Note
Below are the answers for the first two test cases:

题意：
比较容易理解，给你两个a * b的长方形，两个长方形的边必须和所求的正方形的边平行，而且两个长方形不能重合。还不明白的话看图片

思路：
很简单，以较短的边作为侧边y，那么较长的边就为x；所求的正方形的边则为a或者2*b，即为其中较大的那一个，即可求面积。

代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn = 1e7 + 5;
int main()
{
	int t;
	cin >> t;
	int a, b;
	int x, y;
	while (t--)
	{
		cin >> a >> b;
		x = max(a, b);
		y = min(a, b);
		if (y * 2 > x)
			cout << 4 * y * y << endl;
		else
			cout << x * x << endl;
	}
	return 0;
}

B. Honest Coach

来源：http://codeforces.com/contest/1360/problem/B

There are n athletes in front of you. Athletes are numbered from 1 to n from left to right. You know the strength of each athlete — the athlete number i has the strength si.

You want to split all athletes into two teams. Each team must have at least one athlete, and each athlete must be exactly in one team.

You want the strongest athlete from the first team to differ as little as possible from the weakest athlete from the second team. Formally, you want to split the athletes into two teams A and B so that the value |max(A)−min(B)| is as small as possible, where max(A) is the maximum strength of an athlete from team A, and min(B) is the minimum strength of an athlete from team B.

For example, if n=5 and the strength of the athletes is s=[3,1,2,6,4], then one of the possible split into teams is:

first team: A=[1,2,4],
second team: B=[3,6].
In this case, the value |max(A)−min(B)| will be equal to |4−3|=1. This example illustrates one of the ways of optimal split into two teams.

Print the minimum value |max(A)−min(B)|.

Input
The first line contains an integer t (1≤t≤1000) — the number of test cases in the input. Then t test cases follow.

Each test case consists of two lines.

The first line contains positive integer n (2≤n≤50) — number of athletes.

The second line contains n positive integers s1,s2,…,sn (1≤si≤1000), where si — is the strength of the i-th athlete. Please note that s values may not be distinct.

Output
For each test case print one integer — the minimum value of |max(A)−min(B)| with the optimal split of all athletes into two teams. Each of the athletes must be a member of exactly one of the two teams.

Example
inputCopy
5
5
3 1 2 6 4
6
2 1 3 2 4 3
4
7 9 3 1
2
1 1000
3
100 150 200
outputCopy
1
0
2
999
50
Note
The first test case was explained in the statement. In the second test case, one of the optimal splits is A=[2,1], B=[3,2,4,3], so the answer is |2−2|=0.
题意：
把所给的数组分成a和b两个子数组（元素不重复使用），令a数组的的最大值和b数组的最小值的差最小，并输出。

思路：
先不管其他的元素，只关注a的最大值和b的最小值，其实就是找原始数列中两元素的差的最小值；先将数组排序，遍历找相邻的元素差的最小值就ok

代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn = 1e7 + 5;
int a[55];
int main()
{
	int t;
	cin >> t;
	int n;
	while (t--)
	{
		cin >> n;
		for (int i = 1; i <= n; i++)
			cin >> a[i];
		sort(a + 1, a + 1 + n);
		int minn = 0x3f3f3f3f;
		for (int i = 1; i < n; i++)
		{
			int k = a[i + 1] - a[i];
			if (k < minn)
				minn = k;
		}
		cout << minn << endl;
	}
	return 0;
}

C. Similar Pairs

来源：http://codeforces.com/contest/1360/problem/C

We call two numbers x and y similar if they have the same parity (the same remainder when divided by 2), or if |x−y|=1. For example, in each of the pairs (2,6), (4,3), (11,7), the numbers are similar to each other, and in the pairs (1,4), (3,12), they are not.

You are given an array a of n (n is even) positive integers. Check if there is such a partition of the array into pairs that each element of the array belongs to exactly one pair and the numbers in each pair are similar to each other.

For example, for the array a=[11,14,16,12], there is a partition into pairs (11,12) and (14,16). The numbers in the first pair are similar because they differ by one, and in the second pair because they are both even.

Input
The first line contains a single integer t (1≤t≤1000) — the number of test cases. Then t test cases follow.

Each test case consists of two lines.

The first line contains an even positive integer n (2≤n≤50) — length of array a.

The second line contains n positive integers a1,a2,…,an (1≤ai≤100).

Output
For each test case print:

YES if the such a partition exists,
NO otherwise.
The letters in the words YES and NO can be displayed in any case.

Example
inputCopy
7
4
11 14 16 12
2
1 8
4
1 1 1 1
4
1 2 5 6
2
12 13
6
1 6 3 10 5 8
6
1 12 3 10 5 8
outputCopy
YES
NO
YES
YES
YES
YES
NO
Note
The first test case was explained in the statement.

In the second test case, the two given numbers are not similar.

In the third test case, any partition is suitable.

题意：
现有一个定义

• 两个数的奇偶性相同
• 两个数的差的绝对值为1 ，即|a-b|=1

满足以上两个条件之一，就可以说两个数是相似的
先给你一个数组，让你判断数组的元素是否都相似

思路：
由于n为偶数，那么奇数个数和偶数个数奇偶性相同

• 如果都为偶，直接各自配对即可如果都为偶，直接各自配对即可如果都为偶，直接各自配对即可
• 如果为奇，看是否都有一对奇数和偶数相差为1配对，如果找不到就NO

代码：

#include
#include
using namespace std;
typedef long long ll;
int a[110], cnt[110];

int main()
{
    int t;
    cin >> t;
    while (t--) 
    {
        memset(cnt, 0, sizeof cnt);
        int n;
        cin >> n;
        int x = 0, y = 0;
        for (int i = 1; i <= n; i++) 
        {
            cin >> a[i];
            cnt[a[i]]++;
            if (a[i] & 1)x++;
            else y++;
        }
        bool flag = 0;
        for (int i = 1; i <= n; i++)
            if (cnt[a[i] + 1] || cnt[a[i] - 1]) 
            {
                flag = 1; 
                break; 
            }
        if (!flag && (x & 1))
            cout << "NO" << endl;
        else 
            cout << "YES" << endl;
    }
    return 0;
}

D. Buying Shovels

来源：http://codeforces.com/contest/1360/problem/D

Polycarp wants to buy exactly n shovels. The shop sells packages with shovels. The store has k types of packages: the package of the i-th type consists of exactly i shovels (1≤i≤k). The store has an infinite number of packages of each type.

Polycarp wants to choose one type of packages and then buy several (one or more) packages of this type. What is the smallest number of packages Polycarp will have to buy to get exactly n shovels?

For example, if n=8 and k=7, then Polycarp will buy 2 packages of 4 shovels.

Help Polycarp find the minimum number of packages that he needs to buy, given that he:

will buy exactly n shovels in total;
the sizes of all packages he will buy are all the same and the number of shovels in each package is an integer from 1 to k, inclusive.
Input
The first line contains an integer t (1≤t≤100) — the number of test cases in the input. Then, t test cases follow, one per line.

Each test case consists of two positive integers n (1≤n≤109) and k (1≤k≤109) — the number of shovels and the number of types of packages.

Output
Print t answers to the test cases. Each answer is a positive integer — the minimum number of packages.

Example
inputCopy
5
8 7
8 1
6 10
999999733 999999732
999999733 999999733
outputCopy
2
8
1
999999733
1
Note
The answer to the first test case was explained in the statement.

In the second test case, there is only one way to buy 8 shovels — 8 packages of one shovel.

In the third test case, you need to buy a 1 package of 6 shovels.

题意：
想买n个铲子，一共有k种包装，第i种包装里有i个铲子，问如何才能正好买n个铲子，而且买的包书数最少
即
给你一个数n，找一个1−k的数，使得这个数乘p（p为整数）为n，求最小的数p

思路：
直接枚举n的所有因子x，如果这个因子在1−k那么计算一下n/x，并取最小值

代码：

#include
#include
#include
using namespace std;
typedef long long ll;
const ll inf = 0x3f3f3f3f;

int main()
{
    int t;
    cin >> t;
    while (t--) 
    {
        int n, k;
        cin >> n >> k;
        int ans = inf;
        for (int i = 1; i * i <= n; i++) 
        {
            int t = n / i;
            if (n % i == 0 && i <= k)
                ans = min(ans, n / i);
            if (n % t == 0 && t <= k)
                ans = min(ans, n / t);
        }
        cout << ans << endl;
    }
    return 0;
}

E. Polygon

来源：http://codeforces.com/contest/1360/problem/E

Polygon is not only the best platform for developing problems but also a square matrix with side n, initially filled with the character 0.

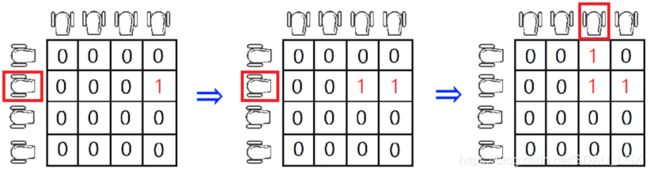
On the polygon, military training was held. The soldiers placed a cannon above each cell in the first row and a cannon to the left of each cell in the first column. Thus, exactly 2n cannons were placed.

Initial polygon for n=4.
Cannons shoot character 1. At any moment of time, no more than one cannon is shooting. When a 1 flies out of a cannon, it flies forward (in the direction of the shot) until it collides with a polygon border or another 1. After that, it takes the cell in which it was before the collision and remains there. Take a look at the examples for better understanding.

More formally:

if a cannon stands in the row i, to the left of the first column, and shoots with a 1, then the 1 starts its flight from the cell (i,1) and ends in some cell (i,j);
if a cannon stands in the column j, above the first row, and shoots with a 1, then the 1 starts its flight from the cell (1,j) and ends in some cell (i,j).
For example, consider the following sequence of shots:

1. Shoot the cannon in the row2. Shoot the cannon in the row 3. Shoot the cannon in column

You have a report from the military training on your desk. This report is a square matrix with side length n consisting of 0 and 1. You wonder if the training actually happened. In other words, is there a sequence of shots such that, after the training, you get the given matrix?

Each cannon can make an arbitrary number of shots. Before the training, each cell of the polygon contains 0.

Input
The first line contains an integer t (1≤t≤1000) — the number of test cases. Then t test cases follow.

Each test case starts with a line containing an integer n (1≤n≤50) — the size of the polygon.

This is followed by n lines of length n, consisting of 0 and 1 — the polygon matrix after the training.

The total area of the matrices in all test cases in one test does not exceed 105.

Output
For each test case print:

YES if there is a sequence of shots leading to a given matrix;
NO if such a sequence does not exist.
The letters in the words YES and NO can be printed in any case.

Example
inputCopy
5
4
0010
0011
0000
0000
2
10
01
2
00
00
4
0101
1111
0101
0111
4
0100
1110
0101
0111
outputCopy
YES
NO
YES
YES
NO
Note
The first test case was explained in the statement.

The answer to the second test case is NO, since a 1 in a cell (1,1) flying out of any cannon would continue its flight further.

题意：
每行左侧和每列上侧有一个炮台，每一时刻可以有一个炮台发出炮弹，炮弹碰到墙壁或者另一个炮弹会停下来并留在原地
问给出的图是否合法问给出的图是否合法问给出的图是否合法

思路：
由于每行左侧和每列上侧有炮台，一个位置想要有炮弹，必须保证他是边界，或者他的下面或右边有一个炮弹使他停止，枚举判断即可

代码：

#include 
#include 
using namespace std;
typedef long long ll;
const int N = 50 + 5;
int n, m, t;
int i, j, k;
char a[N][N];

int main()
{
    cin >> t;
    while (t--)
    {
        cin >> n;
        for (i = 1; i <= n; i++) {
            for (j = 1; j <= n; j++)
                cin >> a[i][j];
        }
        bool flag = 1;
        for (i = 1; i <= n; i++) 
        {
            for (j = 1; j <= n; j++) 
            {
                if (i != n && j != n) 
                {
                    if (a[i][j] == '1') 
                    {
                        if (a[i][j + 1] != '1' && a[i + 1][j] != '1')
                        {
                            flag = 0; 
                            break;
                        }
                    }
                }
            }
            if (!flag) break;
        }
        if (!flag) 
            cout << "NO" << endl;
        else 
            cout << "YES" << endl;
    }
    return 0;
}

G. A/B Matrix

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given four positive integers n, m, a, b (1≤b≤n≤50; 1≤a≤m≤50). Find any such rectangular matrix of size n×m that satisfies all of the following conditions:

each row of the matrix contains exactly a ones;
each column of the matrix contains exactly b ones;
all other elements are zeros.
If the desired matrix does not exist, indicate this.

For example, for n=3, m=6, a=2, b=1, there exists a matrix satisfying the conditions above:

∣∣∣∣010100001010001100∣∣∣∣
Input
The first line contains an integer t (1≤t≤1000) — the number of test cases. Then t test cases follow.

Each test case is described by four positive integers n, m, a, b (1≤b≤n≤50; 1≤a≤m≤50), where n and m are the sizes of the matrix, and a and b are the number of ones for rows and columns, respectively.

Output
For each test case print:

“YES” (without quotes) and the required matrix (if there are several answers, print any) if it exists, or
“NO” (without quotes) if it does not exist.
To print the matrix n×m, print n rows, each of which consists of m numbers 0 or 1 describing a row of the matrix. Numbers must be printed without spaces.

Example
inputCopy
5
3 6 2 1
2 2 2 1
2 2 2 2
4 4 2 2
2 1 1 2
outputCopy
YES
010001
100100
001010
NO
YES
11
11
YES
1100
1100
0011
0011
YES
1
1
G. A/B Matrix

题意：
给定n,m,a,b
你需要找到一个n∗m的矩阵
要求矩阵的每行恰有a个1，每列恰有b个1，其余为0
如果存在构造出来，否则输出−1

题解：
先判断−1的情况
可以用两种情况判断所有1的个数
如果看行，每行有a个1，一共n行，共有n∗a
如果看列，每列有b个1，一共m列，共m∗b
如果这两个不相等，说明不能构造
如果可以构造，那就使每行进行错位构造
第一行构造前a个，第二行继续，如果到了最后一个就重新在第一个构造，直到最后一行

代码：

#include
#include
using namespace std;
typedef long long ll;
int g[100][100];
int main()
{
    int t;
    cin >> t;
    while (t--) 
    {
        int n, m, a, b;
        cin >> n >> m >> a >> b;
        memset(g, 0, sizeof g);
        if (n * a != m * b) 
        { 
            cout << "NO" << endl; 
            continue; 
        }
        cout << "YES" << endl;
        int x = 0;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < a; j++) 
            {
                g[i][x++] = 1;
                if (x == m)x = 0;
            }
        for (int i = 0; i < n; i++, cout << endl)
            for (int j = 0; j < m; j++)
                cout << g[i][j];
    }
    return 0;
}

本人水平有限，若有不足之处，请指正