什么是AVL树?
AVL树即二叉平衡树。因为二叉查找树的形状会受插入数据集的影响,如果数据呈现有序排列,则二叉排序树是线性的,查找算法效率不高。如果我们能保证不管数据是否有序,都能使二叉查找树的高度尽可能的小。这种特殊的二叉查找树即AVL树。具有如下特征:
- 根的左子树和右子树的高度差的绝对值的最大值为1
- 根的左子树和右子树都是AVL树
如果构造AVL树?
查询操作和普通的二叉查找树相同,但是插入节点和删除节点都可能破坏原树的平衡性,所以要考虑每个节点的左子树和右子树的高度差不能超过1,这时可以通过旋转操作来进行修正。
** 插入操作 **
-
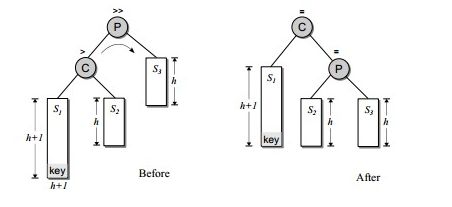
插入节点在P的左孩子的左子树上
处理方式:对P点右旋转处理。如图所示
 图片来自网络.png
图片来自网络.png
python实现右旋转
def right_rotate(node):
'''
右旋转平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 三步完成右旋转操作
node_left = node.left
node.left = node_left.right
node_left.right = node
# 更新节点的高度
node_left.height = max(get_height(node_left.left),
get_height(node_left.right)) + 1
node.height = max(get_height(node.left), get_height(node.right)) + 1
return node_left
-
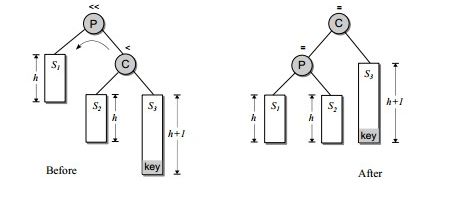
插入节点在P的右孩子的右子树上
处理方式:对P点左旋转处理。如图所示
 图片来自网络.png
图片来自网络.png
python实现左旋转
def left_rotate(node):
'''
左旋转平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 三步完成左旋转操作
node_right = node.right
node.right = node_right.left
node_right.left = node
# 更新节点的高度
node.height = max(get_height(node.left), get_height(node.right)) + 1
node_right.height = max(
get_height(node_right.left), get_height(node_right.right)) + 1
return node_right
-
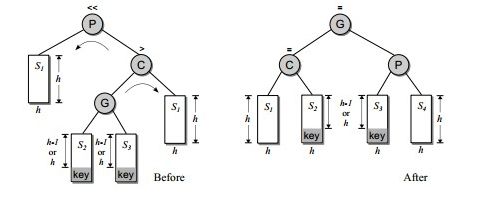
插入节点在P的右孩子的左子树上
处理方式:先对C点做一次右旋转,然后再对P点做一次左旋转。如图所示
 图片来自网络.png
图片来自网络.png
python实现先右旋再左旋
def right_left_rotate(node):
'''
先右旋后右左旋平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 右旋
node.right = right_rotate(node.right)
# 左旋
return left_rotate(node)
-
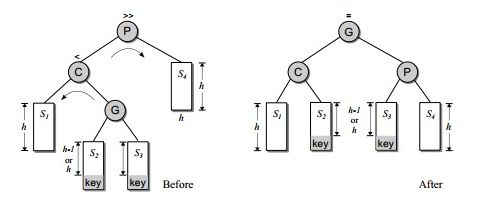
插入节点在P的左孩子的右子树上
处理方式:先对C点做一次左旋转,然后再对P点做一次右旋转。如图所示
 图片来自网络.png
图片来自网络.png
python实现先左旋再右旋
def left_right_rotate(node):
'''
先左旋后右旋平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 左旋
node.left = left_rotate(node.left)
# 右旋
return right_rotate(node)
** 删除操作 **
- 要删除的节点为叶子节点,则直接删除,然后检查该节点的父节点是否平衡,如果不平衡,做平衡化处理
- 要删除的节点只有左儿子或右儿子,则用左儿子或右儿子代替该节点,并做平衡花处理
- 要删除的节点既有左子树又有右子树:如果左子树高度比较高,则选取左子树值最大的节点,将值赋值给当前节点,并删除那个值最大的节点;如果右子树高度比较高,则选取右子树中值最小节点,将值赋值给当前节点,并删除那个值最小的节点。 最后再做平衡化处理
python实现代码
#!/usr/bin/python
# encoding: utf-8
'''AVL树的实现'''
def get_height(node):
return node.height if node else -1
def tree_min(node):
'''找最小值'''
temp = node
while temp.left:
temp = temp.left
return temp
def tree_max(node):
'''找最大值'''
temp = node
while temp.right:
temp = temp.right
return temp
def right_rotate(node):
'''
右旋转平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 三步完成右旋转操作
node_left = node.left
node.left = node_left.right
node_left.right = node
# 更新节点的高度
node_left.height = max(get_height(node_left.left),
get_height(node_left.right)) + 1
node.height = max(get_height(node.left), get_height(node.right)) + 1
return node_left
def left_rotate(node):
'''
左旋转平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 三步完成左旋转操作
node_right = node.right
node.right = node_right.left
node_right.left = node
# 更新节点的高度
node.height = max(get_height(node.left), get_height(node.right)) + 1
node_right.height = max(
get_height(node_right.left), get_height(node_right.right)) + 1
return node_right
def left_right_rotate(node):
'''
先左旋后右旋平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 左旋
node.left = left_rotate(node.left)
# 右旋
return right_rotate(node)
def right_left_rotate(node):
'''
先右旋后右左旋平衡操作
node: 要旋转的节点
return: 旋转后作为根的节点
'''
# 右旋
node.right = right_rotate(node.right)
# 左旋
return left_rotate(node)
def printTree(node):
if node:
print node.key
printTree(node.left)
printTree(node.right)
class Node(object):
def __init__(self, key):
# height为当前节点的高度
self.key = key
self.left = None
self.right = None
self.height = 0
class AVLTree(object):
def __init__(self):
self.root = None
def find(self, key):
'''查找一个值'''
if self.root is None:
return None
else:
# 如果根节点有值,则才真正开始执行查询函数
return self._find(key)
def _find(self, key):
# 真正的查询函数
start = self.root
while start:
if key == start.key:
return start
elif key < start.key:
start = start.left
elif key > start.key:
start = start.right
return None
def insert(self, node):
# 把第一个插入的节点设置为根节点
if self.root is None:
self.root = node
else:
self.root = self._insert(self.root, node)
def _insert(self, index, node):
'''
index: 根节点
node: 要插入的节点
'''
# 递归实现插入
# 递归结束条件
if index is None:
index = node
elif node.key < index.key:
index.left = self._insert(index.left, node)
# 如果左右子树不平衡,则进行平衡操作
if get_height(index.left) - get_height(index.right) == 2:
# 如果插在最左边,则右旋
if node.key < index.left.key:
index = right_rotate(index)
# 如果插在左子节点的右子树上,则先左旋后右旋操作
else:
index = left_right_rotate(index)
elif node.key > index.key:
index.right = self._insert(index.right, node)
if get_height(index.right) - get_height(index.left) == 2:
if node.key > index.right.key:
index = left_rotate(index)
else:
index = right_left_rotate(index)
# 更新高度
index.height = max(get_height(index.left), get_height(index.right)) + 1
return index
def delete(self, key):
# 更新根节点
self.root = self._delete(self.root, key)
def _delete(self, index, key):
'''
index: 根节点
node: 要删除的节点
'''
if key < index.key:
index.left = self._delete(index.left, key)
if get_height(index.right) - get_height(index.left) == 2:
if get_height(index.right.right) > get_height(index.right.left):
index = left_rotate(index)
else:
index = right_left_rotate(index)
index.height = max(get_height(index.left), get_height(index.right))
elif key > index.key:
index.right = self._delete(index.right, key)
if get_height(index.left) - get_height(index.right) == 2:
if get_height(index.left.left) > get_height(index.left.right):
index = right_rotate(index)
else:
index = left_right_rotate(index)
index.height = max(get_height(index.left), get_height(index.right))
# 当要删除的节点左右子树都存在时
elif index.left and index.right:
if get_height(index.left) <= get_height(index.right):
index.key = tree_min(index.right).key
index.right = self._delete(index.right, index.key)
else:
index.key = tree_max(index.left).key
index.left = self._delete(index.left, index.key)
index.height = max(get_height(index.left),
get_height(index.right)) + 1
# 只有左子树或右子树;没有子树
else:
if index.right:
index = index.right
else:
index = index.left
return index
if __name__ == '__main__':
alist = [10, 6, 2, 12, 13, 8]
tree = AVLTree()
for i in alist:
node = Node(i)
tree.insert(node)
printTree(tree.root)
tree.find(8)
tree.delete(8)
print("====分割线====")
printTree(tree.root)
AVL树效率
查找节点:时间复杂度为O(logN)
插入节点:因为需要先查找到节点,然后进行旋转平衡操作(基本为1),所以也为O(logN)
删除节点:再查找到节点之后,还需要检查从删除节点到根节点的平衡因子,所以时间复杂度为O(logN)