SLAM第7章：三角测量
三角测量
- 1. 三角测量
- 2. 使用OpenCV的三角测量
第6章介绍了使用2维点求解相机位姿的方法。二维点丢失了距离信息，能不能求得这些距离能？三角测量可以帮到我们。
1. 三角测量
假设空间点在两个相机坐标系中的三维坐标是 P P P和 P ′ P' P′，如果这两个相机坐标系的变换关系用 R R R和 t ⃗ \vec t t表示，那么：
P = R P ′ + t ⃗ . P = RP' + \vec t. P=RP′+t.
假设 n n n和 n ′ n' n′分别是 P P P和 P ′ P' P′对应的归一化成像平面坐标， z z z和 z ′ z' z′分别是 P P P和 P ′ P' P′到相机光心平面的距离，那么：
z n = z ′ R n ′ + t ⃗ . zn = z'Rn' + \vec t. zn=z′Rn′+t.
上式两边分别与 n n n求外积：
z n × n = z ′ n × R n ′ + n × t ⃗ . zn × n = z'n × Rn' + n × \vec t. zn×n=z′n×Rn′+n×t.
写成矩阵相乘的形式：
z n ^ n = z ′ n ^ R n ′ + n ^ t ⃗ . (7.1.1) zn^{\hat{\quad}} n = z'n^{\hat{\quad}}Rn' + n^{\hat{\quad}} \vec t. \tag{7.1.1} zn^n=z′n^Rn′+n^t.(7.1.1)
公式左边等于0，于是：
z ′ n ^ R n ′ + n ^ t ⃗ = 0. (7.1.2) z'n^{\hat{\quad}}Rn' + n^{\hat{\quad}} \vec t = 0. \tag{7.1.2} z′n^Rn′+n^t=0.(7.1.2)
当我们知道像素坐标时，可以利用相机内参知道归一化成像平面坐标，由第6章还可以知道 R R R和 t ⃗ \vec t t，于是公式 ( 7.1.2 ) (7.1.2) (7.1.2)就可以解得 z ′ z' z′。知道了 z ′ z' z′根据公式 ( 7.1.1 ) (7.1.1) (7.1.1)就可以解得 z z z。
讨论：在第6章已经说过，我们只知道二维坐标，实际距离信息是无法求得的。第6章求得的平移向量 t ⃗ \vec t t的模总是1，缩放系数 α \alpha α无法获得。同样，这里我们求得的 z z z和 z ′ z' z′也是缺少同样的那个缩放系数 α \alpha α。由于是同一个系数，所以如果能知道两个相机的平移距离(光心距离)，那么平移向量和三角测量的结果乘这个系数就可以得到真实距离。
第6章讲的是使用二维坐标求变换，第7章将的是使用二维坐标求距离，这些内容可以用于单目视觉SLAM的初始化：刚开始建图的时候，没有地图，只有两幅图像。第一幅图像对应的第一个相机坐标系为世界坐标系，求第二个相机坐标系到世界坐标系的位姿变换，这个位姿变换称为第二个相机的位姿。我们可以根据第6章求位姿变换，根据第7章求点的距离。这样就可以得到每个二维点在世界坐标系中的坐标。存储的这些三维点(可以包含三维坐标、特征点信息等)称为地图。如果不知道缩放系数 α \alpha α，得到的就是一个比例尺未知的地图。
2. 使用OpenCV的三角测量
#include 我们给 c v : : t r i a n g u l a t e P o i n t s cv::triangulatePoints cv::triangulatePoints的参数是二维的归一化成像平面坐标和两个相机的位姿 T 1 T1 T1和 T 2 T2 T2。
运行结果：
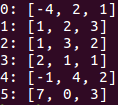只需交换一下参数顺序就可以求出第一个相机坐标系坐标的距离。这里的运行结果和实际值相同，也是因为我们的平移向量 ( 0 , − 1 , 0 ) (0,-1,0) (0,−1,0)的模正好为1。